【总结】最短路
Floyd
- Floyd 是最简单的一种求最短路的算法,用于计算任意两点间的最短路。其时间复杂度为 \(\Theta(n ^ 3)\), 并且它适用于负权图。
算法描述:
- 初始化
- 若两点 \(u\) 和 \(v\) 有一条边,则 \(dis_{u,v} = w_{u,v}\)
- 否则将其赋值为极大值,一边用
0x3f3f3f3f。
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (d[i][j] > d[i][k] + d[k][j])
d[i][j] = d[i][k] + d[k][j];
跑完一遍 Floyd 我们就可以得到的 \(dis_{u,v}\) 就是 \(u\), \(v\) 两点的最短路。
为什么 \(k\) 一定要放在最外层?
由于 Floyd 是采用了动态规划的思想。
由于决策需要枚举中转点,我们可以选择以中转点集为阶段。
\(F_{k, i, j}\) 表示 可以经过标号小于等于 \(k\) 的点中转点 从 \(i\) 到 \(j\) 的最短路。
\(F_{0, i, j}=W_{i, j}\),\(W\) 为邻接矩阵。
\(F_{k, i, j}=\min(F_{k - 1, i, j} , F_{k - 1, i, k} + F_{k - 1, k, j})\)
由于 \(k\) 是 DP 的阶段,所以 \(k\) 所在的循环必须要放在最外层。
输出路径
由于我们定义状态 \(dis_{i, j}\), 所以我们选择定义二维数组 \(pre_{i, j}\) 表示 \(i\) 到 \(j\) 的最短路中 \(j\) 的前驱。
而 \(pre_{i, j}\) 就可以在 Floyd 和 加边时进行赋值:
//Floyd
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dis[i][j] > dis[i][k] + dis[k][j]) {
dis[i][j] = dis[i][k] + dis[k][j];
pre[i][j] = pre[k][j];
}
//加边时的初始化
for (int i = 1; i <= m; i++) {
scanf("%d %d", &x, &y);
dis[x][y] = 1;
pre[x][y] = x;
}
例题
这应该算是 Floyd 的模板了,但是这道题要求我们输出案, 这也是比较简单的。但是这题没有 SPJ, 我们可以发现题目中要求了 请输出字典序最小的一组解。
所以我们在记录 \(pre\) 数组时,必须最小值,来保证输出的是字典序最小的一组解。并且 \(pre_{i, j}\) 记录的不是 \(j\) 的前驱,而是 \(i\) 的后继。
代码如下:
void Floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (dis[i][j] > dis[i][k] + dis[k][j]) {
dis[i][j] = dis[i][k] + dis[k][j];
pre[i][j] = pre[i][k];
}
else if (dis[i][j] == dis[i][k] + dis[k][j] && i != k && pre[i][k] < pre[i][j])
pre[i][j] = pre[i][k];
}
}
void print(int x) {
if (x == t)
return ;
printf("%d ", x);
if (!pre[x][t] || pre[x][t] == t)
return ;
print(pre[x][t]);
}
题意:输出图的一个最小环
我们可以看下面这个例子:
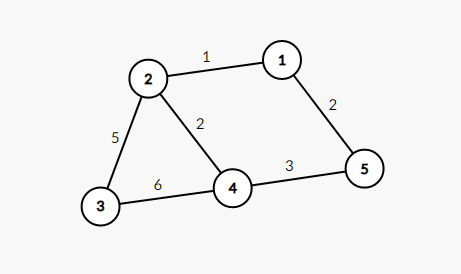
我们很快可以找出它的最小环 1, 2, 4, 5;
我们去掉其他的边在进行观察:
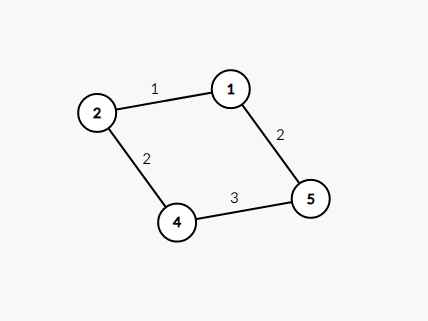
我们不难得出:图中的一个环由一条链,再由另外的一个点链接链的首尾组成。
所以我们就不难写出主要的代码
void Floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i < k; i++)
for (int j = i + 1; j < k; j++)
if (ans > map[i][k] + map[k][j] + d[i][j]) {
ans = map[i][k] + map[k][j] + d[i][j];
cnt = 0;
int t = j;
while (t != i && t) {
path[++cnt] = t;
t = pre[i][t];
}
path[++cnt] = i, path[++cnt] = k;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (d[i][j] > d[i][k] + d[k][j]) {
d[i][j] = d[i][k] + d[k][j];
pre[i][j] = pre[k][j];
}
}
}
Dijkstra
介绍
Dijkstra 算法是基于贪心思想的单源最路算法,可以计算起点到其他点的最短路,但是无法处理负边权;
松弛操作
我们首先来了解一个新的概念:松弛。
当前 \(1\) 到 \(2\) 的最短路是 \(1 -> 2\)。

假设这条边是一条橡皮筋,我们将它放在点 \(3\), 变成下面这个样子。
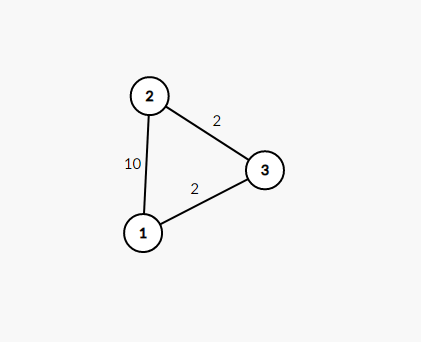
我们可以发现 \(1 -> 3 -> 2\) 的路径更短,也就是说橡皮筋更加的 松弛(虽然不满足三角形三边关系)。
算法实现
定义 \(dis_i\) 表示起点 \(s\) 到点 \(i\) 的最短路长度。
Dijkstra 算法的核心便在于松弛。将点分为蓝白两大阵营,蓝阵营中是已经经过松弛操作确定最短路的点,而白阵营则是没有的。
- 步骤如下
- 在没有被访问过的点中找一个相邻顶点 \(k\),使得 \(dis_k\) 是最小的。
- 将 \(k\) 放进蓝阵营中,即 \(vis_k = 1\)。
- 更新与 \(k\) 相连的每个未确定最短路径(白)的顶点 \(v\),进行松弛操作。
- 具体实现
struct Node {
int e, d;
bool operator < (const Node o) const{
return d > o.d;
}
};
std::priority_queue<Node> q;
void add (int x, int y, int z) {
next[++tot] = head[x], head[x] = tot, ver[tot] = y, edge[tot] = z;
}
void Dijkstra() {
for (int i = 1; i <= n; i++)
dis[i] = 1e9;
q.push({x, 0});
dis[x] = 0;
while (q.size()) {
x = q.top().e;
q.pop();
if (vis[x])
continue;
vis[x] = 1;
for (int i = head[x]; i; i = next[i]) {
int y = ver[i], z = edge[i];
if (dis[y] > dis[x] + z) {
dis[y] = dis[x] + z;
q.push({y, dis[y]});
}
}
}
}
例子
题意:求 \(1\) 到 \(n\) 的最短路。
我们学了 Dijkstra 之后这题就非常简单了,就是一道模板题。
#include <cstdio>
#include <queue>
const int MAXN = 2005, MAXM = 20005;
int n, m;
int head[MAXN], next[MAXM], ver[MAXM], edge[MAXM], tot;
int dis[MAXN];
bool vis[MAXN];
struct Node {
int e, d;
bool operator < (const Node o) const{
return d > o.d;
}
};
std::priority_queue<Node> q;
void add (int x, int y, int z) {
next[++tot] = head[x], head[x] = tot, ver[tot] = y, edge[tot] = z;
}
void Dijkstra() {
for (int i = 1; i <= n; i++)
dis[i] = 1e9;
q.push({1, 0});
dis[1] = 0;
while (q.size()) {
int x = q.top().e;
q.pop();
if (vis[x])
continue;
vis[x] = 1;
for (int i = head[x]; i; i = next[i]) {
int y = ver[i], z = edge[i];
if (dis[y] > dis[x] + z) {
dis[y] = dis[x] + z;
q.push({y, dis[y]});
}
}
}
}
int main () {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z);
add(x, y, z), add(y, x, z);
}
Dijkstra();
printf("%d", dis[n]);
}
Bellman-Ford
介绍
- Bellman-Ford 算法:对每条边执行更新,迭代 \(n - 1\) 次。
- 具体操作是对图进行最多 \(n - 1\) 次松弛操作,每次操作对所有的边进行松弛,为什么是 \(n - 1\) 次操作呢?这是因为我们输入的边不一定是按源点由近至远,万一是由远至近最坏情况就得 \(n - 1\) 次
- 可以应用于负权有向图,但对于负权无向图,它也没有办法。
具体实现
void Bellman_Ford() {
for (int i = 1; i <= n; i++)
dis[i] = INF;
dis[s] = 0;
for (int i = 1; i < n; i++)
for (int j = 1; j <= m; j++)
if (dis[x[j]] + w[j] < dis[y[j]])
dis[y[j]] = dis[x[j]] + w[j];
}
如何判断负环
如果进行了 \(n - 1\) 轮迭代后,应该所有点都是最优,但是如果有两点依旧可以松弛,那么就有负环。
for (int i = 1; i <= m; i++)
if (dis[x[i]] + w[i] < dis[y[i]])
flag = 0;
这个算法其实在 OI 中也没有什么用。
SPFA
在 Bellman-ford 算法中,有许多松弛是无效的。SPFA 算法先将源点加入队列。然后从队列中取出一个点,对该点的邻接点进行松弛,如果该邻接点松弛成功且不在队列中,则把该点加入队列。如此循环往复,直到队列为空,则求出了最短路径。
void spfa() {
for (int i = 1; i <= n; i++)
dis[i] = 1e9;
q.push(x);
dis[x] = 0;
while (q.size()) {
int x = q.front();
q.pop();
vis[x] = 0;
for (int i = head[x]; i; i = nxt[i]) {
int y = ver[i], z = edge[i];
if (dis[y] > dis[x] + z) {
dis[y] = dis[x] + z;
pre[y] = x;
if (!vis[y]) {
vis[y] = 1;
cnt[y]++;
if (cnt[y] >= n) {
printf("-1");
exit(0);
}
q.push(y);
}
} else if (dis[y] == dis[x] + z)
pre[y] = min(pre[y], x);
}
}
}
应用
这里我只选择几道有 价值 的题。只是应为我懒
H 城是一个旅游胜地,每年都有成千上万的人前来观光。为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路。每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,最终到达终点巴士站。
一名旅客最近到 H 城旅游,他很想去S公园游玩,但如果从他所在的饭店没有一路巴士可以直接到达 S 公园,则他可能要先乘某一路巴士坐几站,再下来换乘同一站台的另一路巴士, 这样换乘几次后到达 S 公园。
现在用整数 1 , 2 , … N 1,2,…N1,2,…N 给 H 城的所有的巴士站编号,约定这名旅客所在饭店的巴士站编号为 1 , S 公园巴士站的编号为 N 。
写一个程序,帮助这名旅客寻找一个最优乘车方案,使他在从饭店乘车到 S 公园的过程中换车的次数最少。
很明显在同一线路上的任意两点之间的边权为 \(0\),即设有线路 \(A\) 外一点 \(P\),且 \(P\) 所在线路与线路 \(A\) 有交点,则该点到线路 \(A\) 上交点的边权为 \(1\),进而到达线路 \(A\) 上任意一点边权皆为 \(1\)。
while (m--) {
int x;
char ch;
v.clear();
do {
scanf("%d", &x);
v.push_back(x);
} while(getchar() == ' ');
for (int i = 0; i < v.size(); i++)
for (int j = i + 1; j < v.size(); j++)
h[v[i]][v[j]] = 1;
}
本文来自博客园,作者:zhou_ziyi,转载请注明原文链接:https://www.cnblogs.com/zhouziyi/p/16512197.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号