NOIP2017提高组Day2T3 列队 洛谷P3960 线段树
原文链接https://www.cnblogs.com/zhouzhendong/p/9265380.html
题目传送门 - 洛谷P3960
题目传送门 - LOJ#2319
题目传送门 - Vijos P2033
题意
懒了,不概括了。

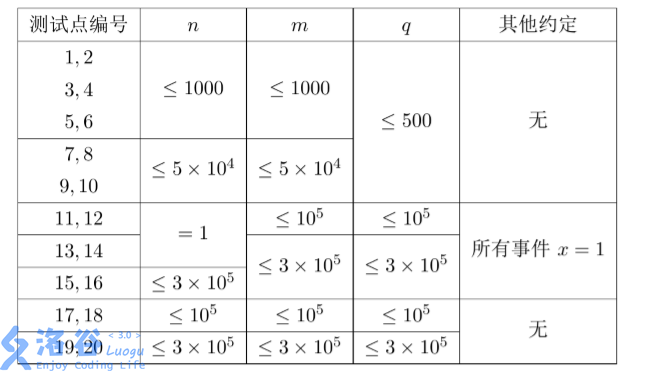
题解
一开始写了树状数组。
算法非常真,写完全部 WA,但是漏了一步,我快写吐了,于是弃疗之后从某度*了一份代码。
我来说说线段树的做法:
线段树动态开点,每行一个线段树,最后一列一个线段树。
线段树要支持找区间第 $k$ 大,这样方便找出指定位置。
注意一下我们会在行或者列线段树新增最多 $q$ 个元素,所以线段树处理的区间要开到 $\max(n,m)+q$ 。
然后就是纯模拟了。注意,无论是在行尾加入新元素,还是在最后一列尾加入新元素,我们都需要记录他们的值,用 $vector$ 存一下。
注意开 $long\ long$ 。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=300005,S=N*20;
int n,m,q,Max,tot;
int root[N],ls[S],rs[S],sum[S];
vector <LL> v[N];
int query(int rt,int L,int R,int x){
if (L==R)
return L;
int mid=(L+R)>>1,tmp=mid-L+1-sum[ls[rt]];
if (x<=tmp)
return query(ls[rt],L,mid,x);
else
return query(rs[rt],mid+1,R,x-tmp);
}
void change(int &rt,int L,int R,int x){
if (!rt)
rt=++tot;
sum[rt]++;
if (L==R)
return;
int mid=(L+R)>>1;
if (x<=mid)
change(ls[rt],L,mid,x);
else
change(rs[rt],mid+1,R,x);
}
LL solve1(int x,LL y){
int pos=query(root[0],1,Max,x);
change(root[0],1,Max,pos);
LL ans=pos<=n?1LL*pos*m:v[0][pos-n-1];
v[0].push_back(y?y:ans);
return ans;
}
LL solve2(int x,int y){
int pos=query(root[x],1,Max,y);
change(root[x],1,Max,pos);
LL ans=pos<m?1LL*(x-1)*m+pos:v[x][pos-m];
v[x].push_back(solve1(x,ans));
return ans;
}
int main(){
scanf("%d%d%d",&n,&m,&q);
Max=max(n,m)+q;
while (q--){
int x,y;
scanf("%d%d",&x,&y);
printf("%lld\n",y==m?solve1(x,0):solve2(x,y));
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号