均摊分析 学习笔记
原文链接www.cnblogs.com/zhouzhendong/p/JunTanFenXi.html
本文概要
1. 引入
2. 简单例子
3. 证明 splay 复杂度
4. 证明 LCT 复杂度
引入
为什么 KMP 不能可持久化,而要用 KMP 自动机来代替?
为什么 splay 不能可持久化,仅仅只是因为难以维护 father 指针吗?
答案是——它们都是基于均摊分析的。
均摊时间复杂度是什么?
这里有一个容易混淆的概念:期望时间复杂度。
期望时间复杂度是指在随机情况下,算法的每种时间复杂度乘上它发生的概率之和。
而均摊时间复杂度不一样。它是指总复杂度在一个范围内,但是单次操作的复杂度并不是总复杂度除以操作数,甚至有可能接近总复杂度。
本文主要部分参照陈胤伯的《均摊分析简介》改写。
简单例子
问题
一个初始值为 0 的 k 位二进制计数器,每次加一。每次加一的运算次数为修改的位数。请问时间复杂度是什么?
证明与答案
作为一个简单例子,自然有很多简单证法。
例如,这个 k 位二进制数第 i 位,需要每加 $2^i$ 次才会变一次。所以所有位的变化次数之和为
$$\sum_i \frac{n}{2^i} = O(n)$$
所以单词操作均摊 $O(1)$ 。
接下来,引入一种更通用的方法——势能分析。
定义势能函数 $\phi$ 表示定义域当前状态的一个函数。
定义 $\phi(i)$ 为第 i 次操作后的状态的势能函数值。
定义第 i 次操作的实际消耗时间为 $t_i$ 。
定义第 i 次操作的均摊时间话费为 $a_i$ ,$a_i = t_i + \phi(i) - \phi(i-1) $ 。
为了方便书写,如不加说明,则用 $\Delta phi$ 表示 $\phi(i)-\phi(i-1)$ 。
于是我们可以用上述定义得到总时间复杂度为
$$\phi(0)-\phi(n)+\sum_{i=1}^{n} a_i$$
接下来回到原先的例子:
定义 $\phi$ 表示当前 k 位二进制数中值为 1 的位的个数,显然第 i 次操作有一个 0 变成 1,设第 i 次操作有 x 个 1 变成 0 。那么
$$a_i=t_i+\Delta\phi = (1+x) + (1-x) = 2$$
所以总时间复杂度为
$$\phi(n) - \phi(0) + \sum_{i=1}^n a_i \leq k + 2n = O(k+n)$$
朴素地讲,我们可以把势能函数看做自己的存款,在耗时的时候消耗以换取时间,在不耗时的时候存储。只要总的变化量在一定范围内,那么总的复杂度就可以被接受。
证明 Splay 的复杂度
相信经过一定的思考,你会发现势能分析的一个关键在于确定合适的势能函数 $\phi$ 。接下来,在证明 splay 复杂度的过程中,你将会体验到势能分析的另一个关键——合理放缩。
定义
设 splay 树的大小和操作次数都是 $O(n)$ 。
定义 $size[x]$ 表示节点 x 的子树大小。
定义函数 $f(x) = \log_2 (size[x])$,接下来简写为 $f(x) = \log (size[x])$ 。注意这个底数 2 是不能忽视的。
定义 $f'(x)$ 表示本次操作之后的 $f(x)$ 。
定义 $\phi = \sum f(x)$ 。
splay 的操作可以分为单旋和双旋,这里定义单次单旋或者双旋的均摊时间花费为 $S(x)$ 。
证明
我们来给旋转操作分成 3 类:
1. 单旋;
2. 双旋 - 先旋 father ,再旋 x;
3. 双旋 - 旋转 x 两次 。
我们来依次证明三种旋转操作的复杂度。下面默认对节点 x 做旋转操作。
单旋

$$\begin{eqnarray*}S(x) &=& 1 + f'(x) + f'(y) - f(x) - f(y) \\ &=& 1 + f'(y) - f(x) \\ &\leq & 1 + (f'(x) - f(x))\end{eqnarray*}$$
双旋 - 先旋 father ,再旋 x
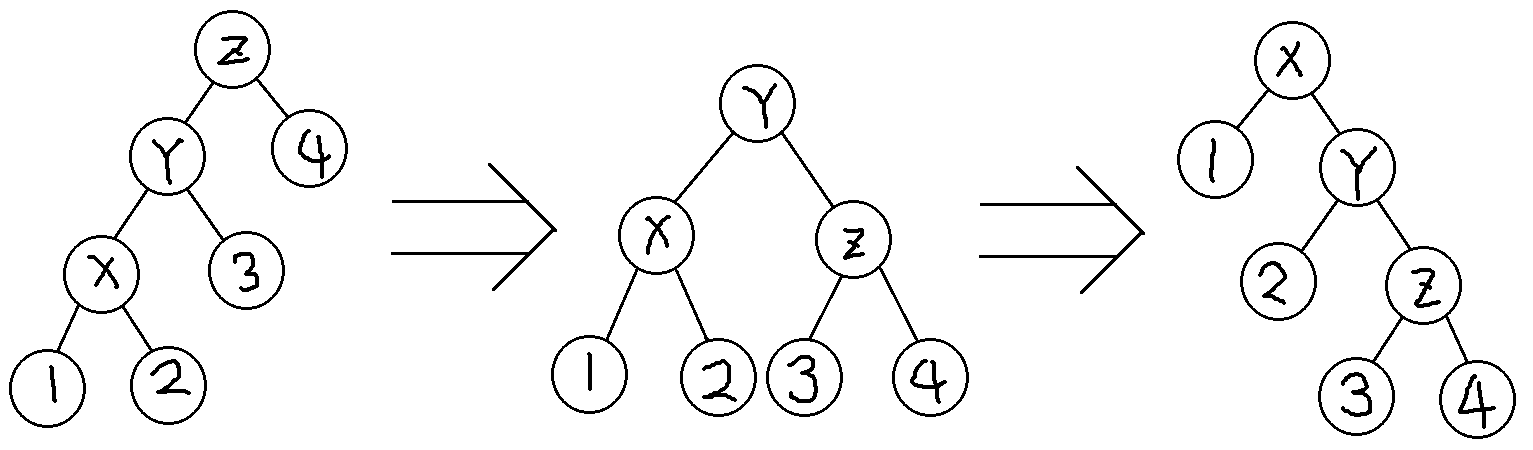
$$\begin{eqnarray*}S(x) &=& 2 + f'(x) + f'(y) + f'(z) - f(x) - f(y) - f(z) \\ &=& 2 + f'(y) + f'(z) - f(y) - f(x) \\ &\leq & 2 + f'(x) + f'(z) - 2f(x) \end{eqnarray*}$$
由于
$$\begin{eqnarray*}f(x) + f'(z) - 2f'(x) &=& \log_2\left(\frac{size[x] \cdot size'[z]}{size'[x] ^2 }\right)\end{eqnarray*}$$
又因为
$$size[x] + size'[z] = size[1] + size[2] + size[3] + size[4] + 2 \leq size'[x] $$
所以
$$size[x] \cdot size'[z] \leq \frac 1 4 size'[x] ^ 2$$
所以
$$f(x) + f'(z) - 2f'(x) \leq \log_2 (\frac 1 4) = -2 $$
即
$$-2 - (f(x) + f'(z) - 2f'(x))\geq 0{\tag 1}$$
将原式加上 (1) 式,得到
$$S(x) \leq 2 + f'(x) + f'(z) - 2f(x) + (-2 - (f(x) + f'(z) - 2f'(x))) = 3(f'(x) - f(x))$$
双旋 - 旋转 x 两次
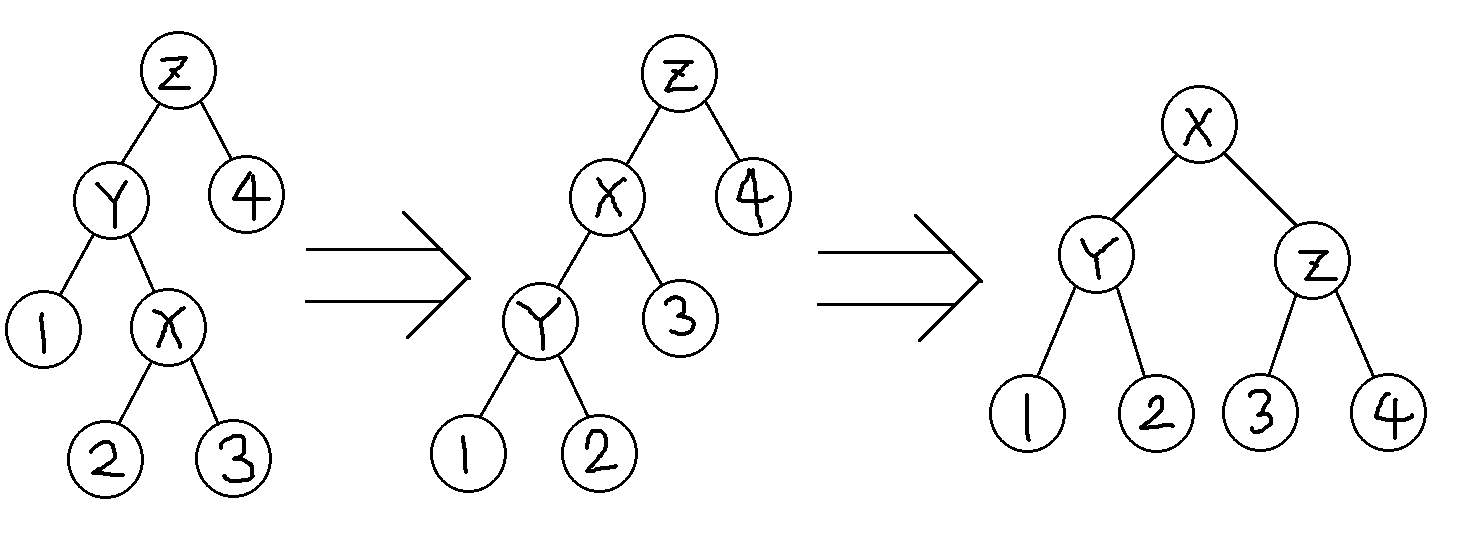
$$\begin{eqnarray*}S(x) &=& 2 + f'(x) + f'(y) + f'(z) - f(x) - f(y) - f(z) \\ &=& 2 + f'(y) + f'(z) - f(y) - f(x) \\ &\leq & 2 + f'(y) + f'(z) - 2f(x) \end{eqnarray*}$$
类似于前一半,我们有
$$-2-(f'(y) + f'(z)-2f'(x))\geq 0$$
于是
$$S(x) \leq 2 + f'(y) + f'(z) - 2f(x) + (-2-(f'(y) + f'(z) - 2f'(x))) = 2(f'(x) - f(x))$$
综上所述,我们可以将三种旋转的单次均摊复杂度分别是
$$1 + (f'(x) -f(x))\\ 3(f'(x) - f(x)) \\ 2(f'(x) - f(x))$$
一次 splay 操作只会做一次 单旋,所以单旋复杂度里的那个多出来的 1 我们可以提出,对最终复杂度贡献 $O(n)$ 。
于是我们把三种操作都放缩到 $3(f'(x) -f(x))$ 。
于是,如果设这次 splay 的起始点为 x,终止点为 y ,那么一次 splay 的均摊复杂度就是 $f(y) - f(x) = O(\log n)$ 。
由于 $\phi(0)$ 和 $\phi(n)$ 都是 $0$~$n\log n$ 范围内的,所以总复杂度为
$$T(n) = \sum_{i=1}^n a_i + \phi(0) - \phi(n) \leq O(n\log n)$$
P.S. 对splay做切割与合并操作时,只要先把连接点旋到根就容易发现势能函数发生变化的节点数是 $O(1)$ 的。
证明 LCT 的复杂度
定义
LCT 的证明和 Splay 类似。这里我们将 $size[x]$ 的定义稍加修改,改成辅助树上 子树 x 的大小。
证明
LCT中splay部分的证明和 Splay 的复杂度证明一样。
这里只考虑虚实链切换时的复杂度。
如果 size[x]*2 >= size[fa[x]] ,那么我们称 x 为 fa[x] 的重儿子,fa[x] 的其他儿子为轻儿子。
那么,显然一个节点在 access 的过程中只会遇见 $O(\log n)$ 个轻儿子。
定义势能函数 $\delta$ 表示实儿子和重儿子不同的节点个数。
考虑一次 access 。
考虑一次 splay 后,当前splay根节点 x 的情况:
1. 如果它是轻儿子,那么消耗 1 时间,势能函数增量小于等于 1 。
2. 如果它是重儿子,那么消耗 1 时间,势能函数减1 。
所以一次access 在轻重链切换上消耗的均摊时间就等于 1. 操作的均摊时间花费,所以一次access的均摊时间复杂度为 $O(\log n)$ 。
所以 $LCT$ 的时间复杂度是
$$O(n\log n)$$
换根、link、cut 的复杂度分析
我们需要证明做这些操作时轻重边变化量合法。
换根
考虑将一个连通块的根从 $x$ 变更为 $y$ 时,哪些边的轻重发生了改变。我们发现,可能改变轻重的边只有 $x$ 到 $y$ 路径上的边,而改变前和改变后这条路径上均只有 $O(\log n)$ 个轻边,所以变化量为 $O(\log n)$。
Link-Cut
考虑 Cut 操作:假设在以 $y$ 为根的连通块上切除子树 $x$,我们发现影响到的也只有 $x$ 到 $y$ 路径上的边,同理变化量还是 $O(\log n)$。
考虑 Link 操作:假设将根为 $x$ 的连通块和根为 $y$ 的连通块通过某两个点相连,我们发现,如果我们取 $x$ 或者 $y$ 为新连通块的根,那么影响到的仍然是连边后 $x$ 到 $y$ 路径上的边,同理变化量还是 $O(\log n)$。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号