单调队列与滑动窗口一

单调队列--滑动窗口最值问题

• 

显然O(n^2)的时间复杂度是无法接受的

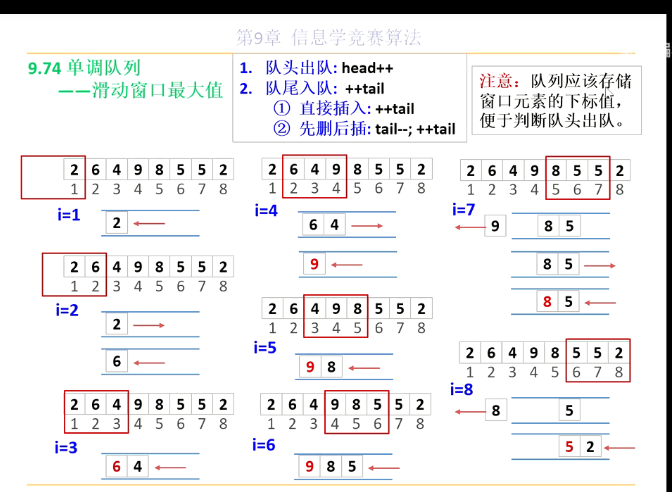
• 我们先考虑滑动窗口滑动过程中最大值的问题

  • 过程即为我们想要维护每个滑动区间的最大值,当新插入一个元素前，我们把这个区间的第一个元素移除,插入新元素，并想在尽可能贴近O(1)的时间内得到该区间的最大值。

  • 这里是十分美妙的想法,借助一个单调队列来模拟上面的场景

    我们在队列头存放第一个预处理区间的最大值,然后降序存着一直到第一个区间末尾的元素(为什么要降序呢❓,这就是这里巧妙模拟的地方)

    后面每次区间移动新进入一个元素,如果该元素小于队尾元素,那么显然它不是最大值,而我们每次移动pop出去的队头元素就是该区间的最大值。

    如果该元素大于队尾元素,那么就不断向前删除队列中小于这个新元素的值(如果全部删除了，那么新插入的元素就是该区间新的最大值)

    还需要考虑的是如果几次插入的值都是小于区间最大值,那么何时队头需要出队，这里可以用pair<int,int> first存储该元素在数组中的下标，通过和当前窗口的的末尾下标做差来判断是否要让该队头元素出列.

    

      ```java
      #include<bits/stdc++.h>
      using namespace std;
      const int N = 1e6+10;
      int n,k;
      //用于存储最大值的下标
      deque<int>q;
      //存最小值xia'biao
      deque<int>p;
      int a[N];
      int main()
      {
          cin>>n>>k;
          for(int i=1;i<=n;i++) cin>>a[i];
         
              for(int i=1;i<=n;i++){
              if(!p.empty()&&p.front()<i-k+1){
                  p.pop_front();
              }
              while(!p.empty()&&a[i]<=a[p.back()]){
                  p.pop_back();
              }
              p.push_back(i);
              if(i>k-1) printf("%d ",a[p.front()]);
          }
          cout<<endl;
          for(int i=1;i<=n;i++){
              if(!q.empty()&&q.front()<i-k+1){
                  q.pop_front();
              }
              while(!q.empty()&&a[i]>=a[q.back()]){
                  q.pop_back();
              }
              q.push_back(i);
              if(i>k-1) printf("%d ",a[q.front()]);
          }
          
          return 0;
      }
      ```