考试心得5
2025/10/3 | 2025CSP-S模拟赛57
https://oj.gxyzh.com/d/hzoj/contest/68d921a11bde45b9248e2bb9/problems
国庆第一天训练。初三牲要死了。搬到机构里训练，效率几乎为零。
T1其实是简单题。但是考场上想了AB性质后就没有想法了，就是把这串数的最终结果求出来，然后给每个原数匹配一个最终数。答案是每个数的增加量乘bi的一种排列的最小值。当时也想到了增加量最大的匹配小的bi的。但是因为一些原因不能直接简单地将原数和最终数匹配（比如必须满足最终数大于等于原数）例如原数列为1 2 2 5，最终数列为1 2 3 5，显然就不能直接将1和5匹配，这样子最后一个5就没的匹配了。
所以我们考虑换个思路 从大到小匹配，在最终数列里面找到第一个大于等于当前数的数字即可。这样就能满足要求了。
T2，当时写了个O(n2)的dp（真的应该是严格的n2啊），但是只能获得O(n^3)的30pts，非常气愤却无果。正解首先是要观察到一个性质，就是最终划分的mex只有一种，这个mex就是全局的mex。证明不说了。然后原来那个dp式子就能写的很简单了。设dp[i]表示以i结尾的划分方案数，如果能满足mex[j][i]等于全局的mex i就能从j转移过来，然后会发现能转移过来的j一定是一段前缀（因为全局的mex一定是大于等于局部的mex的），而且这个前缀也是单调不降的。用单指针求出每个i对应的最右边的j，转移用前缀和优化即可。
T3感觉是很神奇的一道题，它需要用到一个知识点：Kruscal重构树，因为这个树有一个性质就是，任意两点的lca就是他们原图中路径上最大边权最小值。但是我学到的这种解法非常简单直白啊（我总感觉它并不是真正意义上的Kruscal重构树），就是建两棵树，满足如果i是j的祖先i就一定是i到j这条路径上的最大/最小值，然后两棵树各跑一遍，统计在第一棵树里i是j的祖先且在1第二棵树里j是i的祖先的对数即可。
2025/10/5 | 2025CSP-S模拟赛59
https://oj.gxyzh.com/d/hzoj/contest/68e08cb8c65132959724329d/problems
国庆第三天训练（→为了防止自己写错时间）
今天的T1T2还是能学到很多东西的。首先T1是个推式子题，考场上推了2h无果然后放弃。实际上式子确实很难推就是了
2025/10/7 | 2025CSP-S模拟赛60
https://oj.gxyzh.com/d/hzoj/contest/68e22ea8c65132959725404a/problems
放了一天假感觉没什么效果，好像从未走出过“玩没玩好，学没学好”的困境😭
今天的T1还是比较简单的，就是把A和B拆开算，提前算出最初A在式子里的答案（记为res），再处理出m-n+1种B的长为n的段（也就是b在那个式子里贡献的部分），然后最初答案就是res+任意一个B的段的abs的最小值。然后每次修改res都只会+v、-v或不变，找出离他最近的B即可。
T2是一道连续段dp（?）但是LG题解的做法很shen人了。会发现这个平方数是具有传递性的，那么能两两成为平方数的最终会形成一个连通块，然后我们把它看成一种颜色，那么为题就转化为求同种颜色不相邻的方案数。设dp[i][j][k]表示到第i个数，前面和自己不同色的同色相邻有j对，和自己同色和同色相邻有k对的方案数，显然答案是dp[n][0][0]。
转移主要是将当前颜色和上一位颜色是否相同分类讨论，然后再分类讨论当前这一位插到前面已填好的位置之间，大体上有：插到异色之间，插到同色之间，插到两旁。然后去看题解吧。
然后T3其实并不是很会改。但是至少要把50pts的弄懂。考试时以为这是一道数论之类的题
2025/10/19
2025/10/21
2025/10/22 | 2025CSP-S模拟赛65
好像确实欠了很多考试总结了。
https://www.gxyzoj.com/d/hzoj/contest/68f82483cf301c01cdbf5580
这一场死磕T1好久，明明是签到题但我真的做了很久，因为不会算复杂度，想到枚举gcd后觉得直接枚举倍数可能过不去，所以去找倍数的规律（但真的是有规律的啊不信你去找找看如果你找到了固定规律请一定要给我回复！）然后似得比较惨。所以说考试时拼劲全力得分，把觉得对的写上去说不定就过了呢。
T2其实是很简单的题啊，考试时就是这么觉得的，因为扩展后只有最下面一层的子树异或和会改变。但是考场上还是从叶节点的角度开始思考的，所以2q次方个叶节点肯定炸了啊。换个方向，只考虑异或和为x的个数。那修改的时候怎么知道哪些是叶节点呢？好，我们拆开定义两个数组f和g，分别表示叶节点中权值为x的个数，和除叶节点外的子树异或和为x的个数。那么g[i]不仅继承了原来的，还把f[xi]加了进来
（把新右儿子传上去），f[i]不仅继承了原来的（传给了新左儿子），还加上了f[x^i]（新右儿子）。你明白我的意思了吗。
2025/10/23 | 2025CSP-S模拟赛66
https://www.gxyzoj.com/d/hzoj/contest/68fac53acf301c01cdc00d8b/problems
垫底场。虽然好像天天都是垫底场。那我就姑且认为自己是挂分了，呵呵呵。
至少CSP前要保持一个好心态，而不是被s yf阴阳后就内耗了，要外耗！！
T1T2都是很显然的dp但是我就是不会设状态啊，没辙了。然后T1苦思了好久没什么思路就弃了，其实至少也要打一个10分的暴力的，至少也不要挂蛋啊，不要1h啥都没干啊。
然后T2的40还挂了，关键这个样例检查不出来，然后我自以为是地没再检查什么。结果最后犯了一个很纸张的错误，就是添加第j位时，s[j-1]对j也是有影响的。
T3因为没分析清楚复杂度（不止一次干过这种事情了啊）然后第一版打了个暴力，觉得过不了70pts于是写了另一版复杂度稍优一点的暴力（实则跑得更慢）然后最后幡然醒悟去测了下第一版暴力，发现跑得还挺快。于是浪费了1h去做T4。
所以打暴力前要先算好复杂度！！注意读题和数据范围！！
2025/10/25 | 2025CSP-S模拟赛67
https://www.gxyzoj.com/d/hzoj/contest/68fb4db95b0909291f66d23c/problems
这场应该放到最后一天作为信心赛啊，n^2啥都能过。
T1又是算不清复杂度的签到啊，当时想到线段树后以为这道题区间修改复杂度不是log。然后后来自己换了个思路写线段树规避了这个问题，希望下次不要再因为复杂度的问题卡在一道题上1h了。
T2 20分暴力打完fc说找到差异，但我查了好多遍也没找到，结果原来是行末空格的鬼。CSP要注意啊。
然后其实当时觉得40分暴力应该不难打，所以我去补暴力了。
2025/10/28
https://oj.gxyzh.com/d/hzoj/contest/68ff397a5b0909291f68812b/problems
又咕了好久来补考试总结了。今天至少没有前几天挂得惨了。
T1是sb dp题。式子很好推，但赛时只想到了O(n^2m)的做法，然后死活也没有想到怎么优化了。完全没想到m只需要去后n个即可，毕竟只有n种物品！！另数组还开小了，还好没有影响到60pts。。
总结下次想dp优化时要打开思维，不要只专注于数据结构优化、前缀和优化（虽然你也不会写对吧），毕竟这40pts还是 太可惜了。
然后T2赛时瞎猜了个结论就run了，然而这个结论加上暴搜就有60pts的高分！首先很容易发现和≥k的这个环的数如果挨的越近那么逆序对就越少，最好直接连成一个区间。观察w全是非负数的情况，我们肯定希望找到最短的区间和≥k的区间，它的最少逆序对数就是区间长度-1（例如1 2 3 4 5，变成2 3 4 5 1，这样既成环又能减少逆序对。至于证明我显然是不会的呵呵）。然后考虑推广到w有负数的情况，有负数就意味着这个区间的和会减少，为了满足条件一定会增加区间长度，那答案就有可能没有直接从中扣掉几个数更优。首先我们来推一个式子，一个区间[L,R]，区间中没被扣掉的数又cnt个，它最少能形成R-L+R-L+1-cnt个逆序对（就是没有扣数之前的最少逆序对+每一个扣掉的数贡献一个逆序对）。那么我们就可以枚举区间，并维护这个区间最大的cnt，就能使得答案最小。
然后考虑怎么维护这个cnt，拿两个堆，一个小根堆q1一个大根堆q2，q1记录没被扣掉的负数，q2记录被扣掉的负数，那么如果目前这个区间的和小于k（算上当前这个数），就从q1里取出最小的负数把它扣掉（扣掉的数加到q2里面）直至满足条件，然后再在满足条件的情况下从q2里面取出最大的负数加上（也就是把扣掉的数又补回来一点）。尽量使得这个和比k大一点点，也就使得cnt尽量大。
然后T3吧，我成功把%n+1看成%(n+1)，然后怒挂30pts。实际上还把题意理解错了，否则就是75了。正解也是可以拿dfs水过去的，他的复杂度是O(nq)的，8e8，但是有个优化所以跑不满。就是它提前预处理出来两个点能否到达，这样子查询时不用跑所有儿子，只用跑最小的儿子即可。而且判-1也方便了很多。赞。
2025/10/29 | 2025CSP-S模拟赛67
https://www.gxyzoj.com/d/hzoj/contest/68f9b598cf301c01cdbfd5f9/problems
大概写点什么吧，反正快考试了，现在学再多的知识也没什么用，只要不挂分就好（求求了。。。orz）
T1是歪解跑得比正解还快的根号分治题。但根号分治我似乎没有怎么看懂于是我写的是歪解。就是首先拿exgcd优化一下暴力，这样的复杂度应该是O(N^2/q)的，然后加个记忆化，再在求每一组解时加个小优化（就是不合法的话就直接break），然后就卡过去了。跑得挺快。
T2场上只会写一个25pts的dp，但看大家好像也都不怎么会写更高一档的部分分（当然肯定是有的我只是看不懂），25就25吧，正解的SOSdp也不是我能想到的，花费了一个下午死磕代码去理解，感觉应该懂了，但过几天肯定就忘了，代码也不是自己写的，那我改了个什么呢？（发呆ing
然后你看T2就这么难还怎么指望我能在T3 T4上获得多少分呢，当然只会最基础的爆搜啊，结果T3还搜挂了，原因是漏了答案只有1个点的情况。其实考场上的写法特别别扭，当时已经意识到了，但没有造出卡掉自己的样例。所以这告诉我们要打对拍。然后T4除了暴搜还有一个5分白送，但是因为自己没有判断前n-1条边是不是最小生成树就挂了。挂的不多但还是难受啊。。
我能怎么办呢CSP快考完吧CSP快考完吧期中滚一边去吧颓废的实在不行了。
2025/10/30 | 2025CSP-S模拟赛68
https://www.gxyzoj.com/d/hzoj/contest/6901e7b5575f1bcd973a5d78/problems
还是要给CSP前的自己留一个美好的句号。虽然模拟赛还是垫底，但无关紧要啊(✿◡‿◡)
今天的T1是很可爱的小模拟题，6种情况随便写写就可以了。
今天的T2是在考场想到绝望的诈骗题。因为它长得很像01trie，然后我迅速去复习并尝试转移到这个题上，复杂度是O(n3)的，但发现它需要处理出O(n2)个数，但这些数最大可达2^300，肯定炸long long了，怎么办？然后我的01trie就变成最普通的暴力了TT。结果又因为自己加的脑抽特判挂掉了（当时加上判断后忘记测一下样例了），这告诉我们，每一次修改代码后都要测一下，以免发生一些不必要的挂分。
然后我们来看一下真正的O立方37分怎么写，首先是2^300完全不需要处理出来，只需要把它存储成一个字符串，然后插到trie树里面就行，每次找到一个区间，处理出它对应的字符串，补成n位，在trie树里找出对应的最大的字符串（顺便把此时的答案存成字符串），注意到字符串是可以直接比较大小的，每次取max就行了。string真的是很好用的工具啊。
然后我们看正解，正解是比部分分要简单许多的，直接贪心，因为二进制的关系，只要你第一个1的位置（成为fi）保证答案是1，无论后面咋选，都比fi位置答案是0的要大。而且因为它是从01串里面随便取区间，我们肯定是希望fi位置越高越好，那么就找到这个01串的第一个1，并让它右边的第一段1都保持下来，然这些位置的最终答案都是1一定是最优的,。这个fi及后面到n就是我们选的第一个串。然后考虑fi后的第一个0及紧挨这它的那一段0，这一段我们肯定是希望给它配一段1的，就给它配第一个串的开头的那段子串，剩下的写不完了，看题解意会吧。
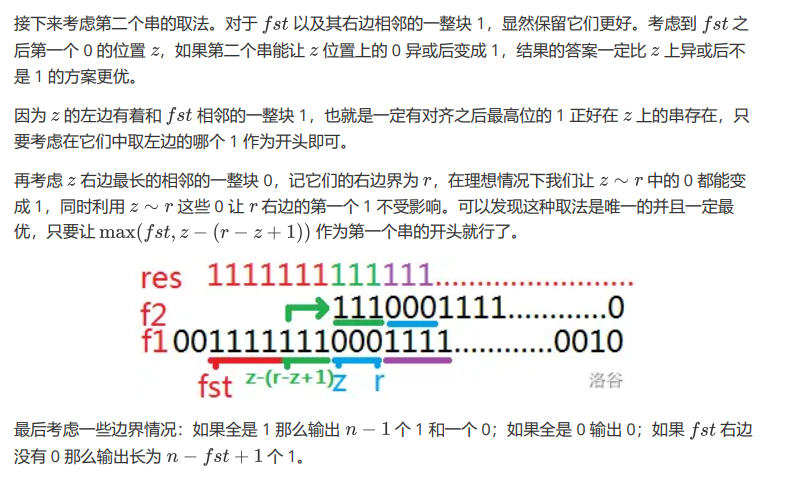
今天的T3是O(n^4)dp可过的哦，放题解：
注意On4能过是加了个优化，看那里要求%3=0才能转移，那我们直接找到第一个%3=0的位置，每次+=3，这样就会跑得快一点。
然后滚动数组千万不要用memset，否则会T到18分。
T4拼尽全力打出了35pts，虽然考试时挂到了20pts，虽然这个题的部分分给的又细又少，虽然35分的代码足足有252行，但是，调出了考场上的代码已经很好了，知足常乐，但愿CSP时所有代码一遍过（大）样例。
祝CSP RP++！加油！！！
2025/11/17 | 2025noip模拟赛77
https://www.gxyzoj.com/d/hzoj/contest/68ea25e932e9dbaccee52159/problems
RP没白加。noip开始停课啦。
然而还是很颓废，只不过这次颓得有点度了。于是开始产粮（来写总结），留着考前吃。CSP考前吃得很香，于是考得也没有很拉。
但依然改变不了我很菜的实事。
说这么多废话有什么用呢？ 今天黄蓝蓝紫，是比CSP简单的，但是考场上卡在T1死活调不出来，其实原因是vector的upper_bound太过于难写了，我瞪眼真找不出来问题，太破防了啊。
然后T1就是很简单的排序+二分题。但是实际上交个暴力就能得105pts。不说啥了。总结：以后尽量不要写vector pair类型的lower/upper_bound。
T2，考虑最终奇位上的数是a，偶位上的是b，记cnt1[i]表示奇位上i的个数，cnt2同样。然后分类讨论：
- 如果任意一个a和b都不相邻
那么答案就是 \(n-cnt1_a-cnt2_b\)
来写T4树根了。。。
首先发现答案有单调性，不难想到二分答案。先考虑暴力，考虑以每个点为根跑一次，然后每次找到深度最深的点并找到它的mid-1级祖先（xmid当前check的答案），把这个祖先的所有儿子删掉（相当于所有儿子的dep都清零）。不断重复这个操作，判断能否在k次操作内使得全树深度最大的点的深度≤mid。整体是一个贪心的思路。他也是满足贪心的性质的。拿线段树维护可以获得55pts。每次check都要建一次树。
然后考虑n个点怎么办。不难想到换根。换根的套路是什么？求出以1为根节点的答案，然后每次只用考虑怎么把父节点的答案改成当前儿子的答案。但因为它是个二分，复杂度又小，所以就不动它了，只用修改线段树到以当前节点为根的状态了。*实际上会发现父亲和儿子的答案最多差1，那么这只log就可以优化掉了）。考虑有什么值是有变化的。设要把根换到u，它的父亲是fa。
- 每个点的dep
就是把u的儿子的dep全-1，其他节点全+1 - x的k级祖先
设u和x在原树上的LCA为lca，那么如果dis(x,lca)比mid小，那么x的k级祖先就是原树上的k级祖先，否则是u的dis(u,x)-mid（实际上代码里还要+1）级祖先。 - x的子树
如果x=u，那么它的子树就是全树。（实际上这一条判不判都行）
如果原树上u在x的子树内，那么x的子树就是除去 u到x路径上x的儿子 的子树 的点。
否则还是原树上的子树。
然后就是check的时候修改一下，但是都要撤销！！！这样子就能避免建树nlogn的复杂度了。
然后我他妈写这道题时犯了3个sb错误，动用学姐的力量一起调了4h+才终于。。调出来两个错误。第三个错误过了两天才找到。不容易啊啊啊啊啊啊啊啊啊。
- 第一个：找u到x路径上x的儿子时大于号打成小于号，我当场爆粗口了。
- 第二个：极大值要选2e9这种稍微小一点的，不要选1e18！！因为这种+-操作容易炸long long！！！
- 第三个：ans[fa]-1没跟1去max，否则就有小于等于0的情况。
终于写完了。
2025/11/18 | NOIP2025模拟赛10
https://hszxoj.com/d/hztg/contest/691459688012802efc87c76b/problems
省流：只有T1可做。但不可读。
考场上4.5h都没有理解T1是啥意思。因为我总以为只要上游有一个排水口，这个排水口以上至更上一点的排水口之间的水都由这个排水口排出。但显然如果这样想是算不出样例的。此时我们应该立马换理解方式而不是固执地以原有的思路去做题！！啊最终还是算不明白于是T1只拿到20pts。实际上读懂题后也就多拿20pts。正解难点还是在于代码实现。我一开始想到的是排水口按时间排序然后一个个遍历，但这样子很难写。应该从水流的角度来考虑。拿一个大根堆或者multiset去存排水口的h，每次取出最大的h，判断n-h这段水流是否可以在到下一个排水口启动之前排完，能排则排。否则相当于又要分一段。然后我放个代码就逃了。
点击查看代码
sort(a+1, a+q+1, cmp);
a[q+1].t=1e18;
ans=a[1].t;
s.insert(a[1].h);
int i=1;
while(n>0)
{
double t;
if(s.size())
t=(n-*s.rbegin())*1.0/s.size();
else t=1e18;
if(t<a[i+1].t-ans)
{
n=*s.rbegin();
ans+=t;
s.erase(*s.rbegin());
}
else
{
n-=(a[i+1].t-ans)*s.size();
ans=a[i+1].t;
if(a[++i].h<n) s.insert(a[i].h);
}
}
2025/11/19 | NOIP2025模拟赛11
省流：我们今天弄懂了T3。鼓掌👏👏👏👏👏👏👏👏👏👏👏👏👏👏👏👏
然后今天的T1是煎蛋题。但AC的只有78个。为什么呢？因为有一种非常讨厌的情况就是我现在要变为全黑的那一行对应的那一列是全白的。我当时想的就是这种情况不合法。但实际上不是的，因为我只要随便找一行有黑的放到那一列全白的就行。所以这种行的答案就是白格数+1。就这种情况要特判一下就行了。
T2仍是不会改的题。
T3感谢T3的数据送了我84-28pts！！因为我写的复杂度实际上是O(n^3)的（虽然跑不满），然后获得了大量分数。考场上的思路其实就是一个贪心，思路就是找到每一个i对应的最远的j使得[i,j]或起来的值是a[i]，记这个j为b[i]，然后找[i+1,n]、[i+2,n]...[b[i]+1,n]中字典序最小的，然后不断往后跳。但好像还没有证伪，但也没有证出来为啥是对的。
然后正解是dp，是一个倒着跑的dp+单调栈二分+hash，就是dp[i]表示[i,n]形成的最终答案序列，然后转移的话就是找到dp[i+1],dp[i+2],dp[i+3]...dp[b[i]+1]中字典序最小的，然后dp[i]就是最小的字典序前面加上a[i]。那么我们需要快速地找出这个最小的序列，于是可以用到单调栈。由于它的单调性，就可以二分出满足在b[i]+1及以前的最小决策序列。具体的，单调栈越往下所存下标对应的dp序列越优，越往下所存的下标越大。然后考虑怎么判断dp序列是否更优，怎么记录答案。其实说白了就是解决怎么记录dp序列并在复杂度不爆炸的情况下维护单调栈的单调性。考虑倍增+hash。设f[x][i]表示x在答案序列往后的2i个数对应在原序列的下标，h[x][i]表示x在答案序列往后的2i个数形成的哈希值。这个哈希值的作用就是辅助找到两个序列里的第一个不同的位置，然后直接比较即可。f数组顺便也记录了答案。就完啦。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define int long long
using namespace std;
const int maxn=2e5+5;
const ull P=13331;
int n, a[maxn], b[maxn], c[maxn], nxt[maxn], f[maxn][20], h[maxn][20], st[maxn];
ull p[maxn];
void add(int x,int y)
{
f[x][0]=y;
h[x][0]=a[x];
for(int i=1;i<18;i++)
{
f[x][i]=f[f[x][i-1]][i-1];
h[x][i]=((ull)h[f[x][i-1]][i-1]*p[(1<<i-1)]+h[x][i-1]);
}
}
bool check(int x,int y)
{
for(int i=17;i>=0;i--)
{
if(h[x][i]==h[y][i]&&f[x][i]&&f[y][i])
{
x=f[x][i], y=f[y][i];
}
}
return y!=n+1&&a[x]<=a[y];
}
signed main()
{
// freopen("min.in","r",stdin);
// freopen("min.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T;
cin>>T;
p[0]=1;
for(int i=1;i<maxn;i++)
{
p[i]=p[i-1]*P;
}
while(T--)
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
int l=n+1;
st[l]=n+1;
for(int i=0;i<30;i++) b[i]=n+1;
for(int i=n;i>=1;i--)
{
int minn=n+1;
for(int j=0;j<30;j++)
{
if(a[i]>>j&1) b[j]=i;
else minn=min(minn, b[j]);
}
add(i, st[upper_bound(st+l,st+n+2,minn)-st-1]);
while(check(i, st[l])) l++;
st[--l]=i;
}
int x=1;
while(x!=n+1)
{
cout<<a[x]<<" ";
x=f[x][0];
}
cout<<"\n";
}
return 0;
}
/*
1
13
0 1 1 0 0 0 1 2 2 3 0 2 3
5
5
0 1 0 1 0
6
1 1 4 5 1 4
7
1 9 1 9 8 1 0
7
7 3 3 5 3 3 4
8
7 3 3 5 3 3 4 8
*/
2025/11/24 | CSP-S模拟赛加赛2
https://www.gxyzoj.com/d/hzoj/contest/68f06cd532e9dbaccee699c1/problems
今天的T1差点没切o_o ....，最后0.5h没有放弃，然后尝试换思路才做出来，所以这告诉我们把问题想简单，不要在一个点上死磕，全方面多想想。
然后T2其实得有假的70pts的，但挂到20pts，原因竟是没加ios、没换"\n"、被卡常TT。然后正解其实特别简单，就是会发现答案不是0，-1，就是1，2，然后如果两个点之间存在长度为奇数的边，那么答案为1，否则答案为2。然后我们的目标就是判断两点之间是否存在长度为奇数或长度为偶数的边。能发现一个性质就是两个点如果到同一个点的距离奇偶性不一样，那么这两个点之间的长度就存在奇数。设f[u][0/1]表示u到它所在连通快的一个节点是否存在奇/偶距离。写一个类似于spfa的bfs即可。
“Days seem sometimes as if they'll never end”
浙公网安备 33010602011771号