扫描线

扫描线一般运用在图形上面，它和它的字面意思十分相似，就是一条线在整个图上扫来扫去，它一般被用来解决图形面积，周长，以及二维数点等问题。

二维矩形面积并问题

在二维坐标系上，给出多个矩形的左下以及右上坐标，求出所有矩形构成的图形的面积。
给每一个矩形的上下边进行标记，下面的边标记为 1，上面的边标记为 -1。每遇到一个水平边时，让这条边（在横轴投影区间）的权值加上这条边的标记。

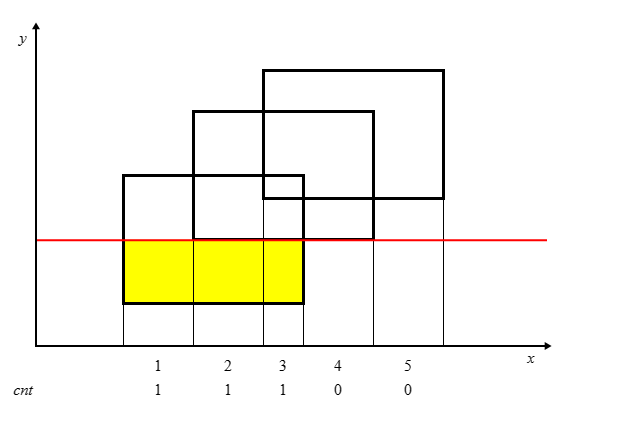
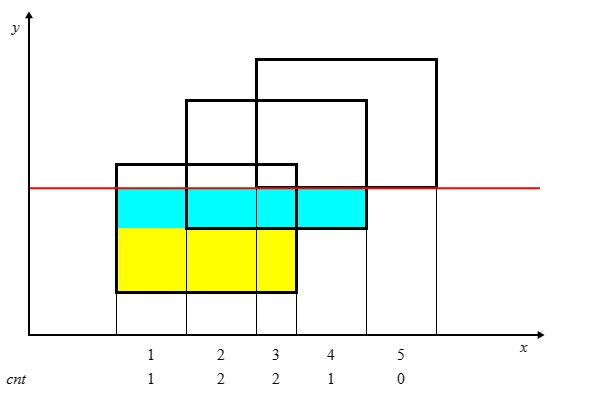
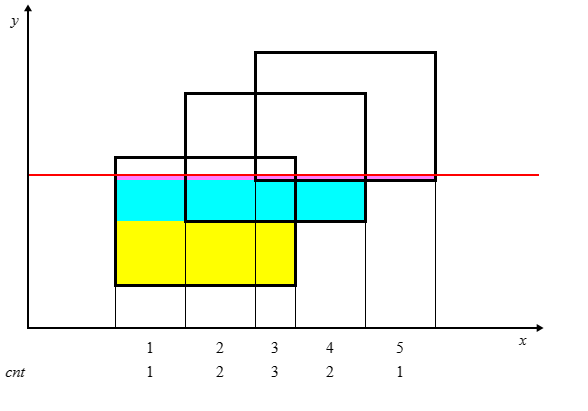
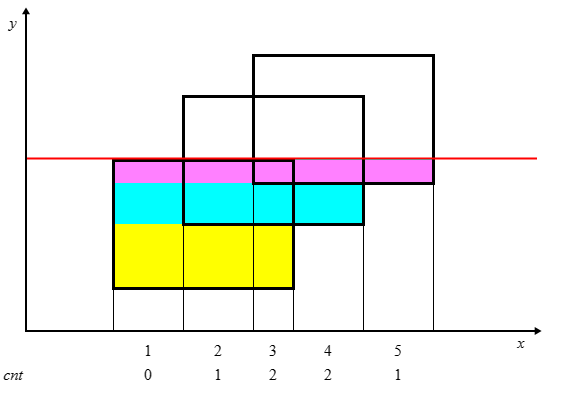
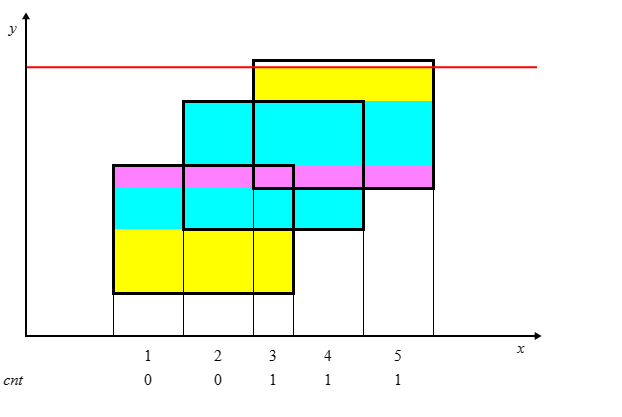
请观察图片中底部数字变化。

所以会发现，要求这些矩形的面积并，只需要求出这些不同颜色的矩形之和。具体的只需要求出他们的长。可以拿线段树维护，具体有两个操作：

1. 一段区间权值加 1、减 1。
2. 统计整个数轴上，区间权值大于 0 的总长度。

例：【模板】扫描线 & 矩形面积并

区间修改，区间覆盖固然拿普通线段树，但可能会写得很复杂。发现每次我们都只想要整个数轴的大于1的长度，即 \(tr[1].len\) ，在update时将pushdown转换到pushup里，直接修改这个区间即可：

void pushup(int id)
{
	int l=tr[id].l, r=tr[id].r;
	if(tr[id].sum)
	{
		tr[id].len=a[r+1]-a[l];//注意这里是r+1哦
	}
	else
	{
		tr[id].len=tr[lid].len+tr[rid].len;
	}
}

注意：这个线段树的每个点不是线段的端点，而是一个线段，因此修改的时候要写成update(1, b[i].x1, b[i].x2-1, b[i].o);，上面代码的r+1同理。

完整代码

#include<algorithm>
#include<iostream>
#define int long long
#define lid id<<1
#define rid id<<1|1
using namespace std;
const int maxn=1e6+5;
int n, a[maxn<<1], t[maxn<<1], tot, ans;
struct sq{
	int x1, x2, y, o; 
}b[maxn<<1];
struct seg_tree{
	int l, r, sum, len;
}tr[maxn<<2];
void pushup(int id)
{
	int l=tr[id].l, r=tr[id].r;
	if(tr[id].sum)
	{
		tr[id].len=a[r+1]-a[l];
	}
	else
	{
		tr[id].len=tr[lid].len+tr[rid].len;
	}
}
void build(int id,int l,int r)
{
	tr[id].l=l, tr[id].r=r;
	if(l==r) return ;
	int mid=(l+r)>>1;
	build(lid, l, mid);
	build(rid, mid+1, r);
}
void update(int id,int l,int r,int val)
{
//	cout<<id<<" "<<tr[id].l<<" "<<tr[id].r<<" "<<l<<" "<<r<<endl;
	if(tr[id].l>=l&&tr[id].r<=r)
	{
	//	cout<<"here"<<endl;
		tr[id].sum+=val;
		pushup(id);
		return ;
	}
	int mid=(tr[id].l+tr[id].r)>>1;
	if(r<=mid) update(lid, l, r, val);
	else if(l>mid) update(rid, l, r, val);
	else
	{
		update(lid, l, mid, val);
		update(rid, mid+1, r, val);
	}
	pushup(id);
}
bool cmp(sq a,sq b)
{
	return a.y<b.y;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x1, y1, x2, y2;
		cin>>x1>>y1>>x2>>y2;
		b[i]={x1, x2, y1, 1};
		b[i+n]={x1, x2, y2, -1};
		a[++tot]=x1, a[++tot]=x2;
	}
	sort(b+1, b+n*2+1, cmp);
	sort(a+1, a+n*2+1);
	int m=unique(a+1, a+n*2+1)-a-1;
	for(int i=1;i<=2*n;i++)
	{
		b[i].x1=lower_bound(a+1, a+m+1, b[i].x1)-a;
		b[i].x2=lower_bound(a+1, a+m+1, b[i].x2)-a;
	} 
	build(1, 1, m);
	ans=0;
	for(int i=1;i<n*2;i++)
	{
		update(1, b[i].x1, b[i].x2-1, b[i].o);
		ans+=(b[i+1].y-b[i].y)*tr[1].len;
	}
	cout<<ans;
	return 0;
}

练1：[poj1151]亚特兰蒂斯

除了xy坐标是反的其他一模一样。

练2：[IOI1998] [USACO5.5] 矩形周长Picture

除了纵向的会求，其他的就不会了呵呵。但是我是真的没想到横向的是两次修改的长度之差，嗯。。

周长并比面积并要麻烦一些，维护的东西变多了（但是横着扫一遍再竖着扫一遍能简单一些）。注意到横着的线段其实就是两次修改的覆盖长度之差，竖着的只需要求出当前有多少个互不相交的覆盖区间2高度，pushup是这样的：

struct seg_tree{
	int l, r, sum, num, len, lo, ro;//lo ro分别表示左端点和右端点是否被覆盖
}tr[maxn<<2];
void pushup(int id)
{
	int l=tr[id].l, r=tr[id].r;
	if(tr[id].sum)
	{
		tr[id].num=1;
		tr[id].len=a[r+1]-a[l];
		tr[id].lo=tr[id].ro=1;
	}
	else if(l==r)
	{
		tr[id].num=tr[id].len=tr[id].lo=tr[id].ro=0;
	}
	else
	{	
		tr[id].len=tr[lid].len+tr[rid].len;
		tr[id].num=tr[lid].num+tr[rid].num;
		if(tr[lid].ro==1&&tr[rid].lo==1) tr[id].num--;
		tr[id].lo=tr[lid].lo;
		tr[id].ro=tr[rid].ro;
	}
}

完整代码

#include<algorithm>
#include<iostream>
#define int long long
#define lid id<<1
#define rid id<<1|1
using namespace std;
const int maxn=1e4+5;
int n, a[maxn<<1], t[maxn<<1], tot, ans;
struct sq{
	int x1, x2, y, o; 
}b[maxn<<1];
struct seg_tree{
	int l, r, sum, num, len, lo, ro;
}tr[maxn<<2];
void pushup(int id)
{
	int l=tr[id].l, r=tr[id].r;
	if(tr[id].sum)
	{
		tr[id].num=1;
		tr[id].len=a[r+1]-a[l];
		tr[id].lo=tr[id].ro=1;
	}
	else if(l==r)
	{
		tr[id].num=tr[id].len=tr[id].lo=tr[id].ro=0;
	}
	else
	{	
		tr[id].len=tr[lid].len+tr[rid].len;
		tr[id].num=tr[lid].num+tr[rid].num;
		if(tr[lid].ro==1&&tr[rid].lo==1) tr[id].num--;
		tr[id].lo=tr[lid].lo;
		tr[id].ro=tr[rid].ro;
	}
}
void build(int id,int l,int r)
{
	tr[id].l=l, tr[id].r=r;
	if(l==r) return ;
	int mid=(l+r)>>1;
	build(lid, l, mid);
	build(rid, mid+1, r);
}
void update(int id,int l,int r,int val)
{
//	cout<<id<<" "<<tr[id].l<<" "<<tr[id].r<<" "<<l<<" "<<r<<endl;
	if(tr[id].l>=l&&tr[id].r<=r)
	{
	//	cout<<"here"<<endl;
		tr[id].sum+=val;
		pushup(id);
		return ;
	}
	int mid=(tr[id].l+tr[id].r)>>1;
	if(r<=mid) update(lid, l, r, val);
	else if(l>mid) update(rid, l, r, val);
	else
	{
		update(lid, l, mid, val);
		update(rid, mid+1, r, val);
	}
	pushup(id);
}
bool cmp(sq a,sq b)
{
	return a.y<b.y;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x1, y1, x2, y2;
		cin>>x1>>y1>>x2>>y2;
		b[i]={x1, x2, y1, 1};
		b[i+n]={x1, x2, y2, -1};
		a[++tot]=x1, a[++tot]=x2;
	}
	sort(b+1, b+n*2+1, cmp);
	sort(a+1, a+n*2+1);
	int m=unique(a+1, a+n*2+1)-a-1;
	for(int i=1;i<=2*n;i++)
	{
		b[i].x1=lower_bound(a+1, a+m+1, b[i].x1)-a;
		b[i].x2=lower_bound(a+1, a+m+1, b[i].x2)-a;
	} 
	build(1, 1, m);
	ans=0;
	int lst=0;
	for(int i=1;i<=n*2;i++)
	{
		update(1, b[i].x1, b[i].x2-1, b[i].o);
		ans+=(b[i+1].y-b[i].y)*2*tr[1].num+abs(tr[1].len-lst);
		lst=tr[1].len;
	}
	cout<<ans;
	return 0;
}

练3：窗口的星星

这道题巧妙的地方在于

---

马克图布。