基环树和笛卡尔树
基环树
基环树是由 \(n\) 个点及 \(n\) 条边组成的连通图,比树多一条边。当然,如果不保证连通,有n个节点、n条边的无向图也有可能是一个基环树森林。
有向基环树又分为内向基环树(每个点入度为1),外向基环树(每个点出度为1)。可以形象地理解为前者是从外指向环的,后者是从环向外指出的。
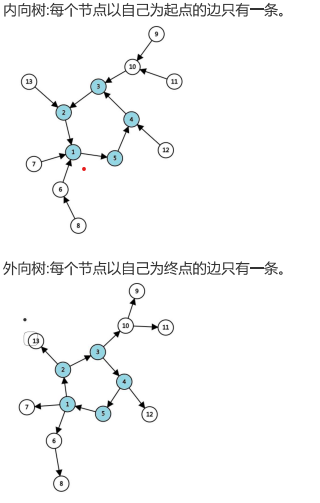
对于有关基环树的问题,一般有两种解决方式:
1. 把环抽出来,这样整个图就变成一个环上面挂了几个子树的样子了,然后对子树进行操作,将信息合并到环上的节点,最后就能把一个图上的问题降到环上处理。
2. 将环断开一条边,然后当作普通树处理。
找环
dfs找环:
void find_circle(int u)
{
dfn[u]=++idx;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa[u]) continue;
if(dfn[v])
{
if(dfn[v]<dfn[u]) continue;
a[++tot]=v;
for(;u!=v;v=fa[v]) a[++tot]=fa[v];
}
else fa[v]=u, find_circle(v);
}
}
拓扑排序找环:
for(int i=1;i<=n;i++)
{
cin>>v[i];
e[v[i]].push_back(i);//vectorli记录的是每个节点的儿子
in[v[i]]++;
}
for(int i=1;i<=n;i++)
{
if(!in[i]) q.push(i);
}
while(q.size())
{
int u=q.front();
q.pop();
if(!--in[v[u]]) q.push(v[u]);
}
for(int i=1;i<=n;i++)
{
if(in[i])
{
//此时的i即为环上的点
}
}
例题:[ZJOI2008] 骑士
考虑将环断开一条边(端点为 \(x,y\)),那么就变成一个普通树形dp了,设 \(dp[i][0/1]\) 表示i节点选或不选的子树最大值,转移很显然。考虑断开的这两条变不能都选,那么从x和y分别跑一次dp,答案即为 \(max(dp[x][0],dp[y][0])\)。
值得注意的一点是这道题会形成基环树森林,所以要从每个点开始都找一遍环,然后处理并累计答案。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+5;
int n, a[maxn], f[maxn], dp[maxn][2], vis[maxn], siz[maxn], flag, ans, x, y, tot;
int head[maxn], edgenum=1;
struct edge{
int next;
int to;
}edge[maxn<<1];
inline void add(int from,int to)
{
edge[++edgenum].next=head[from];
edge[edgenum].to=to;
head[from]=edgenum;
}
inline void dfs(int u,int fa)
{
vis[u]=1;
siz[++tot]=u;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
if(!vis[v]) dfs(v, u);
else if(vis[v]&&!flag)
{
flag=1;
x=u, y=v;//要断的那条边的两个端点
}
}
}
inline void dfs1(int u,int fa)
{
dp[u][0]=0;
dp[u][1]=a[u];
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
dfs1(v, u);
dp[u][0]+=max(dp[v][0], dp[v][1]);
dp[u][1]+=dp[v][0];
}
}
inline void solve()
{
if(!flag)//没有基环树
{
int rt=siz[1];
dfs1(rt, 0);
ans+=max(dp[rt][0], dp[rt][1]);
return ;
}
for(int i=head[x];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==y)//断环
{
edge[i].to=0;
edge[i^1].to=0;
break;
}
}
dfs1(x, -1);
int maxx=dp[x][0];
dfs1(y, -1);
maxx=max(maxx, dp[y][0]);
ans+=maxx;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i]>>f[i];
add(f[i], i);
add(i, f[i]);
}
for(int i=1;i<=n;i++)
{
if(!vis[i])
{
tot=0;
flag=0;
dfs(i, 0);
solve();
}
}
cout<<ans;
return 0;
}
练1:[NOIP 2018 提高组] 旅行
m=n-1的60分很好拿。然后考虑环的部分,枚举断边,然后再跑dfs,输出最小字典序即可。
放一个dfs:
bool dfs(int u,int fa)
{
if(!flag)
{
if(u>ans[cnt]) return 1;
if(u<ans[cnt]) flag=1;
}
vis[u]=1;
ans[cnt++]=u;
for(int i=0;i<e[u].size();i++)
{
int v=e[u][i];
if(v==fa||vis[v]||mp[u][v]==0) continue;
if(dfs(v, u)) return 1;
}
return 0;
}
练2:[IOI 2008] Island
一开始想的环上断一条边做发现复杂度过高,于是果断把问题降到环上,发现只需要求出所有基环树的直径之和即可。对于一棵基环树,它的直径要么经过环,要么不经过。对于后者,设 \(f_u\) 表示从环上节点u到它的子树中任意节点的最大值, \(g_u\) 表示它的子树的直径。那么后者的答案即为 \(max(f[i]+f[j]+dis[i][j])\),考虑优化,处理出环上的前缀和,那么答案就是 \(max(f[i]-s[i]+f[j]+s[j])\),那么只需要记录下最大的 \(f[i]-s[i]\) 和 \(f[j]+s[j]\)即可。但是在 \(s[j]-s[i]<0\) 时,答案为 \(max(f[i]-s[i]+f[j]+s[j]+sum)\)(sum是环上所有边的和),取最大值即可。(其实我觉得我对这句话的理解还不是很深刻)
然后我觉得这个题最精髓的就在于它的代码,真的很简短,简直是题解区里的一股清流。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+5;
int n, w[maxn], flag, v[maxn], f[maxn], g[maxn], in[maxn], ans;
int solve(int u)
{
int p=u;
int sum=w[p], t1=f[p], t2=f[p], ans1=g[p], ans2=-1e9;
u=v[u];
while(p!=u)
{
in[u]=0;
ans1=max(ans1, max(g[u], f[u]+sum+t1));
ans2=max(ans2, f[u]-sum+t2);
t1=max(t1, f[u]-sum), t2=max(t2, f[u]+sum);
sum+=w[u];
u=v[u];
}
return max(ans1, ans2+sum);
}
queue<int> q;
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
in[v[i]]++;
}
for(int i=1;i<=n;i++)
{
if(!in[i]) q.push(i);
}
while(q.size())
{
int u=q.front();
q.pop();
int t=f[u]+w[u];
g[v[u]]=max(g[v[u]], max(f[v[u]]+t, g[u]));
f[v[u]]=max(f[v[u]], t);
if(!--in[v[u]]) q.push(v[u]);
}
for(int i=1;i<=n;i++)
{
if(in[i])
{
ans+=solve(i);
}
}
cout<<ans;
return 0;
}
/*
11
3 8
7 2
4 2
1 4
1 9
3 4
2 3
5 8
8 3
5 8
10 3
*/
练3:[POI 2012] RAN-Rendezvous
考虑分类讨论。
- a和b在不同的基环树里
那么答案肯定为-1。 - a和b在同一个基环树的同一子树里
那么答案显然为他们的lca。考虑用倍增求解。 - a和b在同一基环树的不同子树里
答案有两种情况,分别为这两个子树的根,根据题意输出即可。
考虑如何判断这三种情况,只需要在拓扑找环时给同一个环上的节点染上相同颜色即可,同时处理处该环上节点的子树的各种信息。还有一个细节是处理环上两点距离dis,请看下面的代码。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+5;
int n, k, v[maxn], in[maxn], len[maxn], dis[maxn], rt[maxn], f[maxn][20], dep[maxn], col[maxn], idx, vis[maxn];
vector<int> e[maxn];
queue<int> q;
void dfs(int u,int fa,int d,int t)//处理子树
{
for(int i=0;i<e[u].size();i++)
{
int v=e[u][i];
if(v==fa||in[v]) continue;
dep[v]=d+1;
rt[v]=t;
dfs(v, u, d+1, t);
}
}
void dfs1(int u,int idx,int sum)
{
if(dis[u]) return ;
col[u]=idx;
dis[u]=sum;
len[idx]++;
dfs1(v[u], idx, sum+1);
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x, y);
for(int i=18;i>=0;i--)
{
if(dep[f[x][i]]>=dep[y]) x=f[x][i];
}
if(x==y) return x;
for(int i=18;i>=0;i--)
{
if(f[x][i]!=f[y][i])
{
x=f[x][i], y=f[y][i];
}
}
return f[x][0];
}
bool check(int a,int b,int c,int d)
{
if(max(a, b)!=max(c, d)) return max(a, b)<max(c, d);
if(min(a, b)!=min(c, d)) return min(a, b)<min(c, d);
return a>=b;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++)
{
czhixuyin>>v[i];
e[v[i]].push_back(i);
in[v[i]]++;
f[i][0]=v[i];
}
for(int i=1;i<=n;i++)
{
if(!in[i]) q.push(i);
}
while(q.size())
{
int u=q.front();
q.pop();
if(!--in[v[u]]) q.push(v[u]);
}
for(int i=1;i<=n;i++)
{
if(in[i])
{
rt[i]=i;
dfs(i, 0, 0, i);
if(!col[i])
dfs1(i, ++idx, 1);
}
}
for(int i=1;i<=18;i++)
{
for(int u=1;u<=n;u++)
{
f[u][i]=f[f[u][i-1]][i-1];
}
}
while(k--)
{
int x, y;
cin>>x>>y;
if(col[rt[x]]!=col[rt[y]])
{
cout<<-1<<" "<<-1<<"\n";
}
else if(rt[x]==rt[y])
{
int lca_=lca(x, y);
cout<<dep[x]-dep[lca_]<<" "<<dep[y]-dep[lca_]<<"\n";
}
else
{
int a=rt[x], b=rt[y];
int ans1=dep[x]+(dis[b]-dis[a]+len[col[a]])%len[col[a]], ans2=dep[y]+(dis[a]-dis[b]+len[col[a]])%len[col[a]];
if(check(dep[x], ans2, ans1, dep[y])) cout<<dep[x]<<" "<<ans2<<"\n";
else cout<<ans1<<" "<<dep[y]<<"\n";
}
}
return 0;
}
笛卡尔树
笛卡尔树是一种二叉树,每一个节点由一个键值二元组 (k,w) 构成。要求 k 满足二叉搜索树的性质,而 w 满足堆的性质。如果笛卡尔树的 k,w 键值确定,且 k 互不相同,w 也互不相同,那么这棵笛卡尔树的结构是唯一的。如下图:
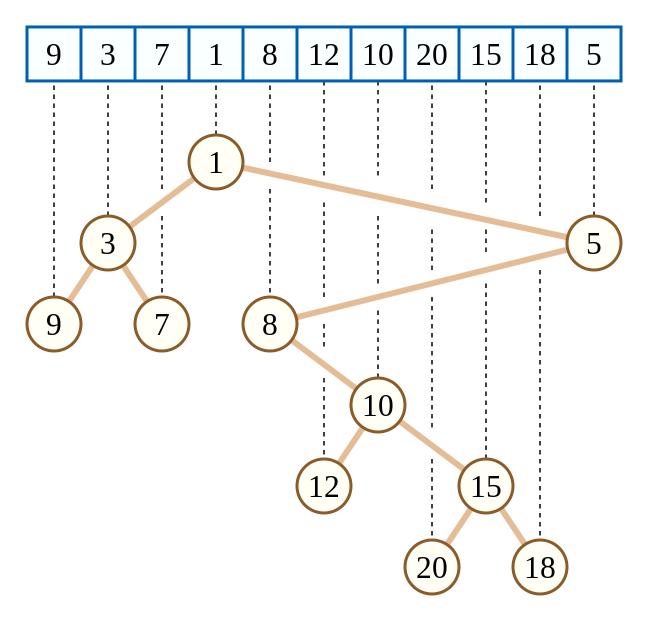
用栈构建笛卡尔树
我们考虑将元素按下标顺序依次插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这棵树的右链(右链:即从根节点一直往右子树走,经过的节点形成的链)的末端。于是我们执行这样一个过程,从下往上比较右链节点与当前节点 u 的 w,如果找到了一个右链上的节点 x 满足 \(w_x<w_u\),就把 u 接到 x 的右儿子上,而 x 原本的右子树就变成 u 的左子树。
图中红框部分就是我们始终维护的右链:
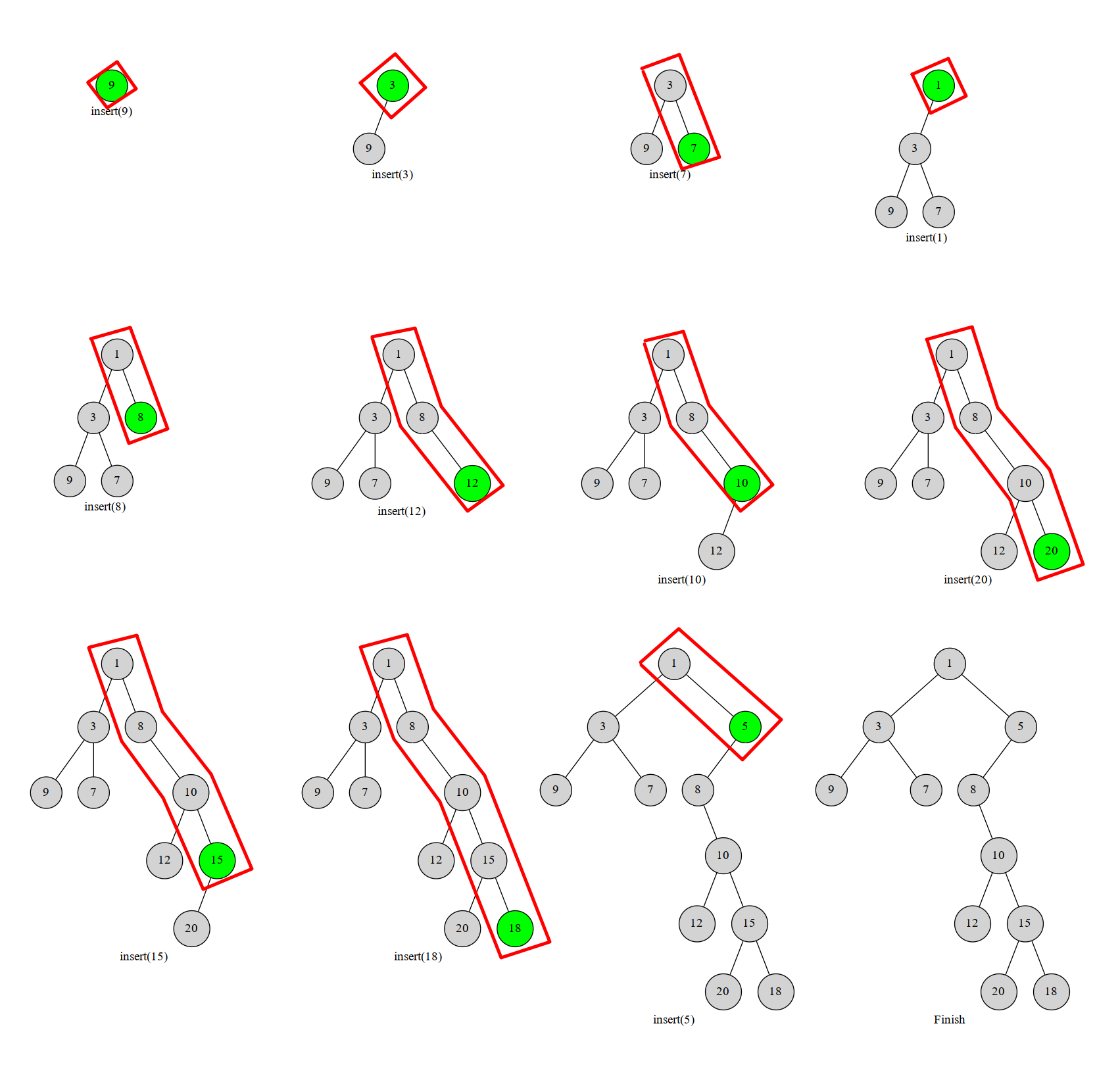
代码:
for(int i=1;i<=n;i++)
{
int k=top;
while(k>0&&w[stk[k]]>w[i]) k--;
if(k) rs[stk[k]]=i;
if(k<top) ls[i]=stk[k+1];
stk[++k]=i;
top=k;
}
练1:[TJOI2011] 树的序
发现这个题刚好是插入顺序满足小根堆,元素的值按照搜索树性质,相当于两者反过来了。所以我们就反过来建树,即把原数列从小到大排序,记录下原来的位置id,建树时判断id的大小。因为是数列,元素的值都不超过n,最后直接前序输出下标即可。
练2:[hdu6305]RMQ Similar Sequence
发现两个序列 RMQ 相似当且仅当他们的笛卡尔树同构。考虑根据给出的A序列把该笛卡尔树建出来,然后算贡献。因为 \(b_i\) 在 0 到 1 之间,故 \(b_i\) 的期望值为 1/2 ,所以 b 序列的和的期望值为 n/2。
对于笛卡尔树的每一棵子树,若用 \(sz[i]\) 表示以 i 为根节点的子树的大小,则满足其根节点是子树的最大值的概率为 \(1/sz[i]\) 。那么总共的概率就是 $\prod_{i=1}^nsz_i $。答案即为两者相乘。
练3:[洛谷 P6453]PERIODNI
神仙题。考虑将格子分割成树。从最底部开始为根,自下而上分成二叉树,就长这样子,分治建树即可:
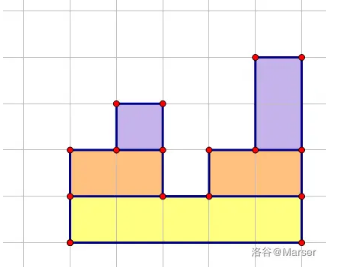
如果不能分成恰好两棵子树,其实没有影响,把某两个放到一起先当成一个节点下一次分开来就好了,没>有必要特别判这个问题。
建树代码
inline int build(int l,int r)
{
if(l>r) return 0;
int minn=1e9, p=0;
for(int i=l;i<=r;i++)
{
if(a[i]<minn)
{
minn=a[i];
p=i;
}
}
int lid=build(l, p-1), rid=build(p+1, r);
h[lid]=a[lid]-a[p], h[rid]=a[rid]-a[p];
w[p]=r-l+1;
ls[p]=lid, rs[p]=rid;
return p;
}
设 \(dp[u][i]\) 表示以u为根的子树里放i个数字的方案数,显然最后的答案为 \(dp[rt][k]\),但因为他的根是个矩形不好转移,考虑再设一个dp状态 \(dp1[u][i]\) 表示以u为根的子树(除了u这个矩形)的方案数,显然 \(dp1[u][i]=\sum_{i=1}^{m}\sum_{j=0}^{i} dp[ls[u]][j]*dp[rs[u]][i-j]\)。所以dp的转移方程即为:\(dp[u][i]=\sum_{i=1}^m\sum_{j=0}^iC_{h_u}^{i-j}*C_{w_u-j}^{i-j}*(i-j)!*dp1[u][j]\)。
大小为 n×m 的棋盘,放入 k 个棋子,互不攻击的方案数为 \(C_n^k*C_m^k*k!\)
可以说是dp的转移是分为根和子树两部分的,dp1的转移是分为左右两个子树两部分的。
练4:[hdu4125]Moles
板子题,注意到题目里说的是按照给出的序列的下标为堆键值,序列值为二叉搜索树的键值排,那不就跟练1是一样的嘛,然后再跑一个kmp就好了。
警钟撅烂:char数组清空要从0开始清!!!不能只清长度



 浙公网安备 33010602011771号
浙公网安备 33010602011771号