人工智能之深度学习基础——反向传播（Backpropagation）

反向传播（Backpropagation）

反向传播是神经网络的核心算法之一，用于通过误差反传调整网络参数，从而最小化损失函数。它是一种基于链式法则的高效梯度计算方法，是训练神经网络的关键步骤。

1. 反向传播的基本步骤

1.1 前向传播

在前向传播过程中，输入数据从输入层经过隐藏层传递到输出层，计算出模型的预测值 y_pred和损失值 L。

1.2 损失计算

损失函数（如均方误差或交叉熵）衡量模型的预测值与真实值之间的差异：

L=Loss(y_pred​,y_true​)

1.3 反向传播

根据链式法则（用于处理复合函数求导的重要规则），计算损失函数相对于每个参数的梯度 ∂L/∂w，从输出层向输入层逐层反向传播。

1.4 参数更新

利用梯度下降等优化算法，通过梯度信息更新每层的权重和偏置：

w=w−η⋅∂w/∂L​

其中：

• w：参数；
• η：学习率。

2. 反向传播的数学推导

2.1 神经网络的层间关系

假设神经网络的某一层：z^(l)=W^(l)a^(l−1)+b^(l) 

　　　　　　　　　　 a^(l)=f(z^(l))

其中：

• z^(l)：隐藏层的线性输出；
• W^(l)：权重矩阵；
• b^(l)：偏置向量；
• a^(l)：激活值；
• f：激活函数。

2.2 损失函数

损失函数（Loss Function）是机器学习和深度学习中用来衡量模型预测结果与真实值之间差距的一个函数。它的值越小，说明模型的预测结果与真实值越接近。损失函数是模型优化的核心部分，它为模型参数的调整提供了依据。

这里以均方误差为例：

m这里是总个数。

2.3 输出层梯

输出层的误差：

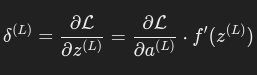
（实际上是把z^(l)=W^(l)a^(l−1)+b^(l) (传递)套入损失函数（L）求的复合函数求导。）

其中：

这里是链式求导的损失函数处步骤。

2.4 隐藏层梯度

隐藏层的误差通过链式法则传播：

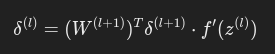
简而言之，就是底层（l+1）的输出层误差求出来了，能推出上一层(l)的误差。上一层的激活函数的导数乘以这一层的权重和误差。

2.5 梯度计算

权重和偏置的梯度为：

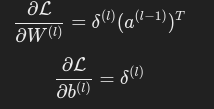
 把z^(l)=W^(l)a^(l−1)+b^(l) 套入损失函数的多元函数求导。

3. 反向传播的流程

1. 前向传播：计算每一层的线性输出 z^(l)、激活值 a^(l)，直到输出层。
2. 计算损失：使用目标函数（如交叉熵、均方误差）计算预测值与真实值的差距。
3. 反向传播：
   • 从输出层开始，计算每一层的误差 δ^(l)；
   • 通过误差传播公式，将误差逐层传递至输入层。
4. 更新参数：利用梯度下降算法更新每层的权重 W^(l) 和偏置 b^(l)。

4. 反向传播的简单例子

问题

构造一个简单的单隐藏层神经网络，输入数据 x=[0.5,0.1]，目标输出 y_true=0.6，激活函数使用 Sigmoid。

模型结构

1. 输入层：2 个神经元。
2. 隐藏层：2 个神经元。
3. 输出层：1 个神经元。

参数初始化

 

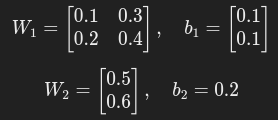
 计算步骤

 σ这里是SIgmoid函数，即激活函数

 

 

————————————————————————————————————————————————

反向传播求导详细计算

 

反向传播的核心是计算损失函数对网络参数的梯度，即 ∂L/∂W​ 和 ∂L/∂b。以下详细解析各步骤的求导，逐步展开每个公式的由来。

1. 网络的定义详解

 单隐藏层神经网络

 

 

 

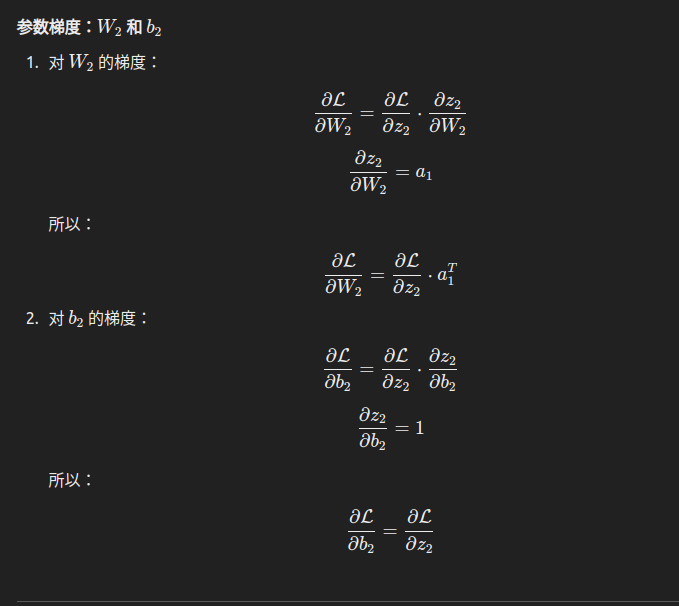
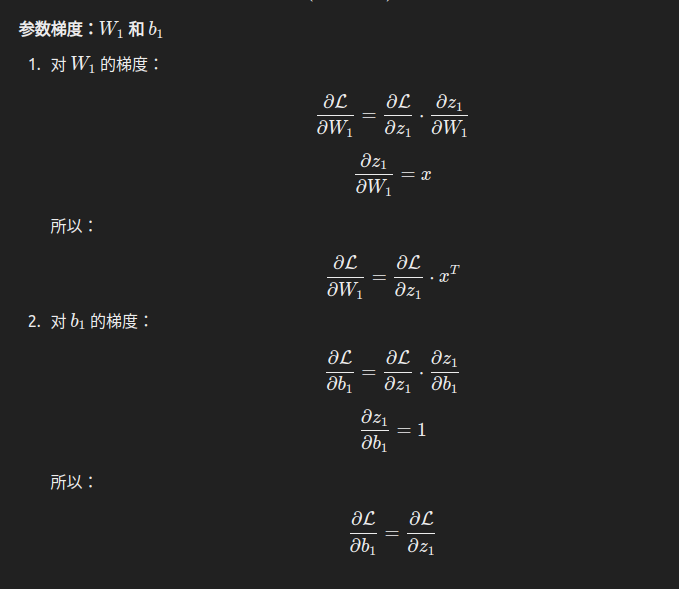
 总结

反向传播通过链式法则逐层计算梯度，并利用梯度下降法更新网络参数，最终最小化损失函数。反向传播算法是现代深度学习的基石，结合优化算法（如 SGD、Adam）可以高效训练复杂的神经网络模型。