人工智能之机器学习线代基础——矩阵分类

1. 按维度和大小

 

方阵（Square Matrix）：

 

行数和列数相等的矩阵。

 

列矩阵（Column Matrix）：

 

只有一列的矩阵。

 

行矩阵（Row Matrix）：

 

只有一行的矩阵。

 

零矩阵（Zero Matrix）：

 

所有元素均为 0。

 

单位矩阵（Identity Matrix）：

 

对角线为 1，其他元素为 0 的方阵。

 

对角矩阵（Diagonal Matrix）：

 

只有对角线元素非零，其余元素为 0。

 

标量矩阵（Scalar Matrix）：

 

对角矩阵且对角线元素相同。

 

稀疏矩阵（Sparse Matrix）：

 

大部分元素为零的矩阵。

2. 按元素取值

实矩阵（Real Matrix）：

元素全为实数。

复矩阵（Complex Matrix）：

元素为复数。

整数矩阵（Integer Matrix）：

元素全为整数。

二值矩阵（Binary Matrix）：

元素为 000 或 111。

正矩阵（Positive Matrix）：

所有元素均为正数。

 

3. 按对称性

 

对称矩阵（Symmetric Matrix）：

转置后等于自身，即 A^T=A。

反对称矩阵（Skew-Symmetric Matrix）：

转置后等于自身的负数，即 A^T=−A。

正交矩阵（Orthogonal Matrix）：

转置矩阵等于逆矩阵，即 A^TA=I。

厄米特矩阵（Hermitian Matrix）：

转置共轭矩阵等于自身，即 A^H=A。

 

反厄米特矩阵（Skew-Hermitian Matrix）：

转置共轭矩阵等于自身的负数，即

A^H=−A。

 4. 按矩阵行列式

奇异矩阵（Singular Matrix）：

行列式为 0 的矩阵，不可逆。

非奇异矩阵（Non-Singular Matrix）：

行列式非零的矩阵，可逆。

5. 按秩

满秩矩阵（Full Rank Matrix）：

矩阵的秩等于其最小维度。

降秩矩阵（Rank-Deficient Matrix）：

矩阵的秩小于其最小维度。

6. 按应用和特殊结构

上三角矩阵（Upper Triangular Matrix）：

主对角线以下的元素全为 0。

下三角矩阵（Lower Triangular Matrix）：

主对角线上方的元素全为 0。

带状矩阵（Band Matrix）：

仅对角线附近的元素非零。

哈达玛矩阵（Hadamard Matrix）：

元素为 +1+1+1 或 −1-1−1，且行列正交。

托普利茨矩阵（Toeplitz Matrix）：

每条斜对角线上的元素相同。

循环矩阵（Circulant Matrix）：

每一行是前一行元素循环右移一次。

 

7. 按特征值和特征向量

正定矩阵（Positive Definite Matrix）：

所有特征值均为正数。

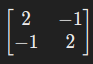
半正定矩阵（Positive Semi-Definite Matrix）：

所有特征值均非负。

负定矩阵（Negative Definite Matrix）：

所有特征值均为负数。

酉矩阵（Unitary Matrix）：

其特征值的模为 1。

总结

矩阵分类可以从维度、对称性、行列式、特征值、结构等多个角度进行划分。熟悉这些分类有助于根据问题选择合适的矩阵工具和方法来简化计算或分析问题。