2020年9月22日 - 课程

2020年9月22日 - 课程

集训安排

组别	上午	下午
J	J模拟赛	初赛讲解
S	S模拟赛	专题训练
J+S	J模拟赛	S模拟赛

最短Hamilton路径

给定一张 \(n\) 个点的带权无向图，点从 0~n-1 标号，求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。

输入格式

第一行输入整数\(n\)。

接下来\(n\)行每行\(n\)个整数，其中第\(i\)行第\(j\)个整数表示点\(i\)到\(j\)的距离（记为a[i,j]）。

对于任意的\(x,y,z\)，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]>=a[x,z]。

输出格式

输出一个整数，表示最短Hamilton路径的长度。

数据范围

\(1 \le n \le 20\)
\(0 \le a[i,j] \le 10^7\)

输入样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

输出样例：

18

解析

1. i代表路径的状态，j代表经过第几个点
   F[1,0]初始状态
   F[2ⁿ-1,n-1]结束
   \[F\left[i,j\right] = \min{(F\left[\ i \operatorname{xor}\ (1<<j),k\ \right]+\operatorname{weight}_{k,j}\ )} \]

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int f[1 << 20][20], weight[20][20], n;

int hamilton(int n, int weight[20][20]) {
	memset(f, 0x3f, sizeof(f));
	f[1][0] = 0;
	for (int i = 1; i < 1 << n; i++)
        //dp的阶段，从二进制角度来看，从经过（出发）第一个i，到所有点都经过
        //j是刚刚定义的点（目前的位置）
        for (int j = 0; j < n; j++) if (i >> j & 1)//如果在i表示的状态中，j点的位置恰好为1
			for (int k = 0; k < n; k++) if ((i^1<<j) >> k & 1)
				f[i][j] = min(f[i][j], f[i^1<<j][k]+weight[k][j]);
    			//以为你j是刚经过的，此处使用取反代表j的位置没有经过
    			//i的状态符合：
    			//1. j点位置是0
    			//2. k点位置为1
    			//upd答案	
	return f[(1 << n) - 1][n - 1];
    //达到便捷，第一维度代表状态全1
    //第二维度代表所有点都经过了
}
//所有的状态 i，所有的状态里面符合条件的是j,k
//j位置上1，i状态中，j位置是1
//之前的状态j=0,k=1
int main() {
	cin >> n;
	for(int i = 0; i < n; i++)
		for(int j = 0; j < n; j++)
			scanf("%d", &weight[i][j]);
	cout << hamilton(n, weight) << endl;
}

291. 蒙德里安的梦想

求把\(N*M\)的棋盘分割成若干个\(1*2\)的的长方形，有多少种方案。

例如当\(N=2,M=4\)时，共有5种方案。当\(N=2,M=3\)时，共有3种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数N和M。

当输入用例\(N=0，M=0\)时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

\(1≤N,M≤11\)

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
int n, m;
long long f[12][1 << 11];
bool in_s[1 << 11];

int main()  {
	while (cin >> n >> m && n) {//读入
		for (int i = 0; i < 1 << m; i++) {
            //集中检查合法的整数，连续的0的长度是偶数
			bool cnt = 0, has_odd = 0;
			for (int j = 0; j < m; j++)//枚举整数i的二进制形式的每一位
				if (i >> j & 1) has_odd |= cnt, cnt = 0;
				else cnt ^= 1;
            	//hasodd记录曾经出现过的cnt
            	//反转奇偶状态
			in_s[i] = has_odd | cnt ? 0 : 1;//只有hasodd和cnt都是0才符合条件
		}
		f[0][0] = 1;
		for (int i = 1; i <= n; i++)
			for (int j = 0; j < 1 << m; j++) {
				f[i][j] = 0;
				for (int k = 0; k < 1 << m; k++)
					if ((j&k) == 0 && in_s[j | k])
						f[i][j] += f[i - 1][k];
			}
		cout << f[n][0] << endl;
	}
}

292 炮兵阵地

司令部的将军们打算在\(N*M\)的网格地图上部署他们的炮兵部队。一个$N*M的地图由N行M列组成，地图的每一格可能是山地（用”H” 表示），也可能是平原（用”P”表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

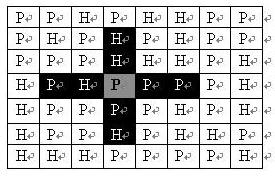
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符(‘P’或者’H’)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

数据范围

\(N≤100,M≤10\)

输入样例：

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出样例：

6

Code

/**
 * @Author:      H S-J
 * @DateTime:    2018-04-18 20:10:21
 * @Description: 
 */
#include <iostream>
#include <cstring>
using namespace std;
#define MST(a, b) memset(a, b, sizeof(a));
#define CLR(a) MST(a, 0);
#define rep(x, y, z) for (int x = y; x < z; ++x)
const int INF = 0x3f3f3f3f;
int dp[101][77][77];
int sg[101];
int n, m, idx;
int s[77]; //合法摆放的集合
int cnt0[77]; //合法摆放方案的具体摆放个数, 即二进制下1的个数
int get_one(int x) {
	int cnt = 0;
	while(x) x &= (x-1), ++cnt;
	return cnt;
}
bool ok(int x) {
	// 相邻两个P之间要有两个H
	if(x & (x << 1)) return false;
	if(x & (x << 2)) return false;
	return true;
}
void init() {
	idx = 0;
	int end = 1 << m;
	rep(i, 0, end) if(ok(i)) {
		// s保存合法方案的集合
		s[idx] = i;
		// cnt0保存合法方案的摆放个数, 二进制位1的个数
		cnt0[idx++] = get_one(i);
	}
}
bool valid(int i, int x) {
	if(sg[i] & x) return false;
	return true;
}
int solve() {
	int ans = 0;
	MST(dp, -1);
	dp[0][0][0] = 0;
	rep(j, 0, idx) if(valid(1, s[j])) {
		dp[1][j][0] = cnt0[j];
		// 考虑n==1情况
		ans = max(ans, dp[1][j][0]);
	}
	rep(i, 2, n+1) {
		// valid()函数判断, 第i行, 用方案s[j]是否合法
		rep(j, 0, idx) if(valid(i, s[j])) {
			// i行跟i-1行的方案, 满足, 互相炸不到对方
			rep(k, 0, idx) if(valid(i-1, s[k]) && (s[j]&s[k])==0) {
				int last = 0;
				// i-2行同上
				rep(l, 0, idx) if(dp[i-1][k][l] != -1 && (s[l]&s[j])==0 && valid(i-2, s[l])) {
					last = max(last, dp[i-1][k][l]);
				}
				dp[i][j][k] = max(dp[i][j][k], last + cnt0[j]);
				if(i == n) ans = max(ans, dp[i][j][k]);
			}
		}
	}
	return ans;
}
int main(int argc, char const *argv[]) {
	ios::sync_with_stdio(0);cin.tie(0);
	cin >> n >> m;
	rep(i, 1, n+1) rep(j, 0, m) {
		char tmp; cin >> tmp;
		if(tmp == 'H') sg[i] |= (1 << (m-1-j));
	}
	init();
	cout << solve() << endl;
	return 0;
}