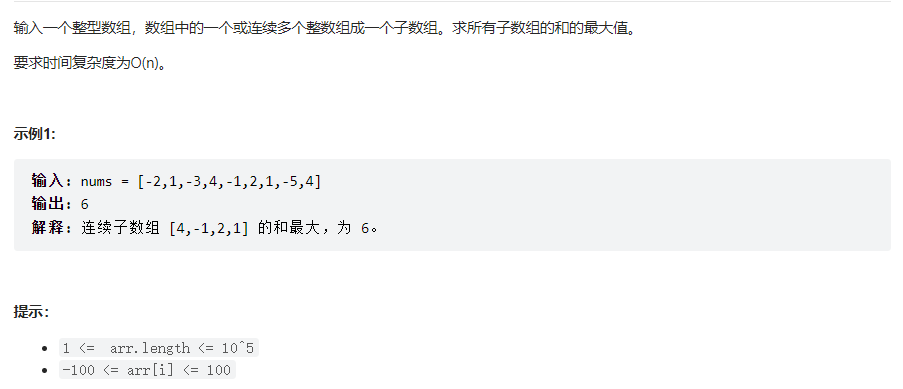
题目描述
思路
动态规划+自下而上
记录每个元素对应的包含了当前元素的连续和的最大值,最后取一个全局最大的
自下而上的话就没有必要保留,一边求一边更新即可
递归的话也可以不用记录,弄一个全局变量实时更新
状态转换方程:f(n)=f(n-1)+nums[n]>nums[n]?f(n-1)+nums[n]:nums[n]
边界:f(0)
最优子结构:f(n-1)
重叠子问题:无
代码实现
class Solution {
public int maxSubArray(int[] nums) {
int result=Integer.MIN_VALUE;
int cur=-101;//这里会参与运算,避免过于极限越界
for(int num:nums){
cur=num+cur>num ? num+cur:num;//
result=cur>result ? cur:result;
}
return result;
}
}
复杂度分析
时间复杂度
O(N)
空间复杂度
O(1)
反思不足
思路
如果不确定递推式,不如自己列几个试试看,别光想
审题
连续子数组不一定从0开始
连续子数组的和是指元素的和,而不是所有子数组的和
想到的是之前的最大值和新加入之后与前面的连续数的最大值之间的最大值
但是超时了,想一想是不是没利用好重复元素
java se
范围越界
为了不对第一个元素特殊讨论设置一个极值,但如果其会参与运算的话,极值不能刚刚好到极限
可以根据题目的条件来确定最小值
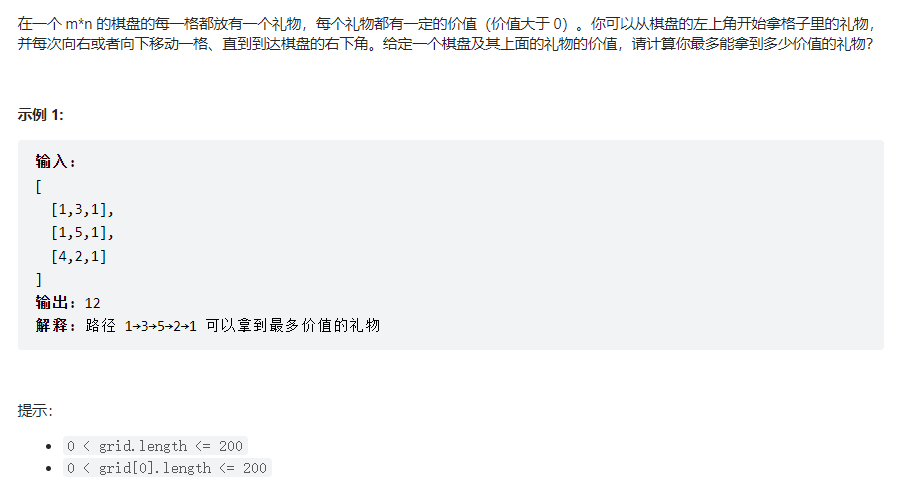
礼物的最大价值
题目描述
思路
动态规划状态转换方程的确定可以通过抵达最后目标的方式来切入,比如那个乌龟上楼梯也是这样
动态规划+递归+哈希表
参考题解切入后自己的思路
分别求从左抵达和从上抵达的最大值,取最大,递归至边界点0,0,由于由于有可能会有重复计算,所以用一个哈希表来存储每个点对应的最大值,于是空间复杂度爆炸
时间复杂度感觉上是O(MN),但是与大佬答案差距很大
动态规划+原地修改+自下而上
可以把每个点的最值直接赋值给该点,于是空间复杂度小了
代码实现
动态规划+递归+哈希表
class Solution {
HashMap<String,Integer> hashMap= new HashMap<String,Integer>();
public int maxValue(int[][] grid) {
return r(grid,grid.length-1,grid[0].length-1);
}
public int r(int [][]grid,int i,int j){
if(i<0||j<0){
return 0;
}
if(!hashMap.containsKey(i+"+"+j)){
int l=r(grid,i,j-1),t=r(grid,i-1,j);
int result=(l>t?l:t)+grid[i][j];
hashMap.put(i+"+"+j,result);
}
return hashMap.get(i+"+"+j);
}
}
动态规划+原地修改+自下而上
class Solution {
public int maxValue(int[][] grid) {
int h=grid.length,l=grid[0].length;
for(int i=0;i<h;i++){
for(int j=0;j<l;j++){
if(i==0&&j==0){
continue;
}else if(i==0){
grid[i][j]+=grid[i][j-1];
}else if(j==0){
grid[i][j]+=grid[i-1][j];
}else{
grid[i][j]+=grid[i][j-1]>grid[i-1][j]?grid[i][j-1] :grid[i-1][j];
}
}
}
return grid[h-1][l-1];
}
}
//进一步优化冗余判断
//但是还是不能到百分百
class Solution {
public int maxValue(int[][] grid) {
int h=grid.length,l=grid[0].length;
for(int i=1;i<h;i++){
grid[i][0]+=grid[i-1][0];
}
for(int j=1;j<l;j++){
grid[0][j]+=grid[0][j-1];
}
for(int i=1;i<h;i++){
for(int j=1;j<l;j++){
grid[i][j]+=grid[i][j-1]>grid[i-1][j]?grid[i][j-1] :grid[i-1][j];
}
}
return grid[h-1][l-1];
}
}
复杂度分析
时间复杂度
O(MN)
空间复杂度
O(MN)
O(1)
反思不足
思路
参考题解思路切入后,没能想到可以原地修改,虽然AC了但是空间复杂度过高,时间复杂度虽然一个量级但还是有差距
而且是用递归做的,一开始并不能清晰的确定出如何自下而上
审题
没有考虑允不允许原地修改



