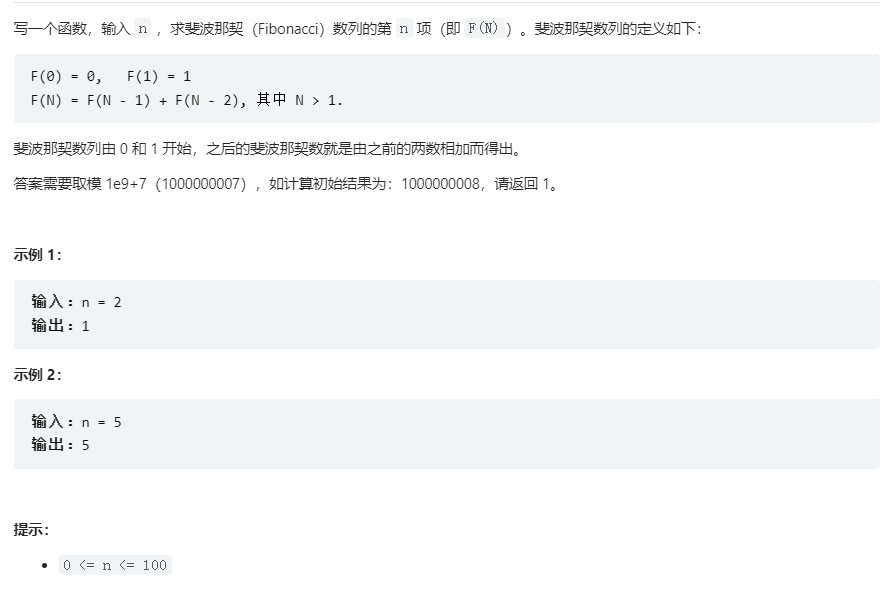
斐波那契数列
题目描述
思路
动态规划+哈希表+递归
动态规划
维基百科定义:
动态规划(英语:Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
最核心思想
拆分子问题+记住过往+避免重复计算
避免重复计算可以用哈希表,前提是有重复计算
典型特征
最优子结构、状态转移方程、边界、重叠子问题。
- f(n-1)和f(n-2) 称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2)就称为状态转移方程
- f(1) = 1, f(2) = 2 就是边界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
每层递归返回f(n-1)+f(n-2),并且取余后加入哈希表中备忘
取余也是有分配律的,并且多次取余都是同一个结果
并且一定要在计算得到结果之前取余,不然会越界
特殊点0和1根据题目处理
动态规划+自底向上
从底往上求,直到抵达需要求的数为止
这种方法就没必要用哈希表来避免重复计算了,不断累加即可
代码实现
动态规划+哈希表+递归
class Solution {
HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
public int fib(int n) {
if(n<2){
return n;
}
if(!map.containsKey(n)){
int num=fib(n-1)+fib(n-2);
map.put(n,num%1000000007);
}
return (map.get(n));
}
}
动态规划+自底向上
class Solution {
public int fib(int n) {
if(n<2){
return n;
}
int a=0,b=1;
int cur=2;
int result=0;
while(cur<=n){
result=(a+b)%1000000007;
a=b;
b=result;
cur++;
}
return result;
}
}
复杂度分析
时间复杂度
二者均为O(N)
空间复杂度
用哈希表的为O(N),不用的为O(1)
反思不足
思路
使用自下而上时,没意识到根本不需要保存较早的值,直接往后推,求和即可。下次遇到动态规划的问题可以多想一下这个问题
审题
没看到题目要求,答案要取模
要取余没能想到运算过程中也可能造成越界,只能在运算过程中取余
青蛙跳台阶问题
题目描述

思路
同斐波那契数列
求多少种可能性的,并且告诉了边界的,大概率是有递推性质的
本题中状态转移方程的理解,根据最后一步跳的阶数来切入,如果为1,则有f(n-1)种,为n,则有f(n-2)种,加起来即可
- f(n-1)和f(n-2) 称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2)就称为状态转移方程
- f(1) = 1, f(2) = 2,f(0)=1 就是边界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
代码实现
动态规划+自底向上
class Solution {
public int numWays(int n) {
if(n==0){
return 1;
}
if(n<=2){
return n;
}
int cur=3;
int a=2,b=1;
int result=0;
while(cur<=n){
result=(a+b)%1000000007;
b=a;
a=result;
cur++;
}
return result;
}
}
复杂度分析
时间复杂度
同斐波那契数列
空间复杂度
同斐波那契数列
反思不足
思路
没能想出来状态转移方程
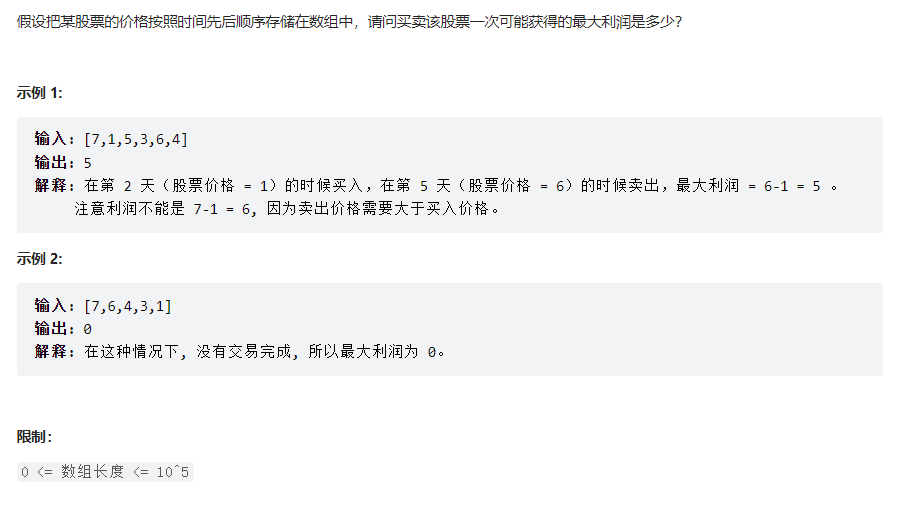
股票的最大利润
题目描述
思路
这类最大利润的题,通常都是要往动态规划的角度去向
动态规划+自底向上
状态转移方程:
maxProfit(n)=max(price(n)-minPrice(n),maxProfit(n-1))
minPrice(n)=min(price(n),minPrcie(n-1))
最优子结构:
maxProfit(n-1)、minPrcie(n-1)
边界:
maxProfit(0)、minPrice(0)
重叠子元素:
无
动态规划+递归
代码实现
动态规划+自底向上
class Solution {
public int maxProfit(int[] prices) {
//如果我们改一下初值,就可以避免这一步判断,然后就超过100%了
if(prices.length==0){
return 0;
}
//过去的最小价格
int lPrice=prices[0];
//过去的最大利润
int mProfit=0;
for(int i=1;i<prices.length;i++){//数组的for循环遍历有点不熟悉啊
lPrice=prices[i]<lPrice ? prices[i]:lPrice;
mProfit=prices[i]-lPrice>mProfit ? prices[i]-lPrice:mProfit;
}
return mProfit;
}
}
class Solution {
public int maxProfit(int[] prices) {
//如果我们改一下初值,就可以避免这一步判断
//过去的最小价格
int lPrice=Integer.MAX_VALUE;
//过去的最大利润
int mProfit=0;
for(int i=0;i<prices.length;i++){//数组的for循环遍历有点不熟悉啊
lPrice=Math.min(lPrice,prices[i]);
mProfit=Math.max(mProfit,prices[i]-lPrice);
}
return mProfit;
}
}
class Solution {
public int maxProfit(int[] prices) {
int cost = Integer.MAX_VALUE, profit = 0;
for(int price : prices) {
//这里三元运算符更好,空间复杂度更低
cost = Math.min(cost, price);
profit = Math.max(profit, price - cost);
}
return profit;
}
}
动态规划+递归
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0){
return 0;
}
return r(prices,1,prices[0],0);
}
public int r(int[]prices,int i,int l,int m){
int result=0;
if(i<prices.length){
l=prices[i]<l?prices[i]:l;
m=prices[i]-l>m?prices[i]-l:m;
result=r(prices,i+1,l,m);
}else{
result=m;
}
return result;
}
}
复杂度分析
时间复杂度
均为O(N)
空间复杂度
递归O(N),其他O(1)
反思不足
思路
刚开始理不清思路,知道这类题可以用动态规划,但是没分析出状态转化方程,要理解记住这类求利润题的状态转换方程
java se
Math
Math.min()返回两者之间的最小值
Math.max()返回两者之间的最大值
Integer
Integer.MAX_VALUE整数上限



