二维数组的查找
题目描述

思路
二叉搜索树法
如果对二叉搜索树比较熟悉,你就会发现改数组有二叉树的特征,于是就可以采用二叉树找值的算法
应用在本题中,如果目标数比标志数大,就行+1,小则列-1,循环终止条件为不匹配,且要变动的索引抵达边界
代码实现
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
if(matrix.length==0){
return false;
}
int n=matrix.length-1,m=matrix[0].length-1;
for(int i=0,j=m;i<=n&&j>=0;){
if(target>matrix[i][j]){
i++;
}else if(target<matrix[i][j]){
j--;
}else{
return true;
}
}
return false;
}
}
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
int i = matrix.length - 1, j = 0;
//正是这一步让其不用判定是否为空数组
while(i >= 0 && j < matrix[0].length)
{
if(matrix[i][j] > target) i--;
else if(matrix[i][j] < target) j++;
else return true;
}
return false;
}
}
复杂度分析
时间复杂度
O(M+N),最坏情况行列都走一边,在对角
空间复杂度
O(1)
反思不足
思路
有序想到二分法,想到先行后列,先列后行,二者都来一遍,4次二分
但是对于条件的判断比较模糊,行之后,如何确定列的索引? 答案是直接返回右指针
参考了题解的二叉搜索树思路后,没有考虑到传递一个空数组的情况,于是索引越界了
以后见到有序的二维数组要把往二叉搜索树方向上想
旋转数组的最小数字
题目描述

思路
二分法
具体细节看代码注释吧,记住二分法是种思想,不要执着于判定条件的变化
记住这种旋转数组的特性,左排列一定全部大于等于右排列
代码实现
class Solution {
public int minArray(int[] numbers) {
int left=0,right=numbers.length-1;
int mid=left+(right-left)/2;
while(left!=right){
//前两步很好理解,目的是找到旋转点,也即边界点,mid大于right时,mid肯定在左,小于right,肯定在右,而且可能处于边界点,所以不-1
//不用到left与mid比较是因为有right足够,这两者唯一能确定的是在mid小于left时,mid肯定在右
if(numbers[mid]<numbers[right]){
right=mid;
}else if(numbers[mid]>numbers[right]){
left=mid+1;
//原始处理方案:right-=1
//等于时,如果mid落在左,且right不处于边界,-1可能遇到更小值,于是往right靠,right处于边界,后续也只会让right不断等于mid,最终与left相等,而一旦mid落在左,那么就必然left到mid都是同一个值,所以返回的还是最小值
//如果mid落在右,那right肯定不处于边界,-1更新mid,继续缩小范围,且此时肯定有mid到right相等
}else{
//新方案:
//一大片连续的相等,让二分查找失去了意义,于是遍历更直接
//1.1时肯定要么找到一个更小值,要么找到边界值也是right,1.2时,找不到更小值,返回的仍是最小值,2时同1.1
int r=left;
for(int i=r+1;i<right;i++){
if(numbers[i]<numbers[r]){
r=i;
}
}
return numbers[r];
}
mid=left+(right-left)/2;
}
return numbers[left];
}
}
复杂度分析
时间复杂度
平均O(log2N),极端情况,所有元素都相同时,会变成O(N),此时只会让right一个一个减,减到left,即0
空间复杂度
O(1)
反思不足
思路
最开始的思路是二分法+递归,但是发现不对,单纯是想到了很久很久之前做过的题,把它背出来而已
知道应该往二分法的角度思考,但是不知道应该怎么分,什么时候终止,什么时候左右指针变动
看了题解才知道,原来恒有左大于右的性质,而最小值就是边界点、旋转点
看了题解仍是做不出来,甚至理解其思路都费了老大劲,好在磕磕绊绊理解了
第一个只出现一次的字符
题目描述
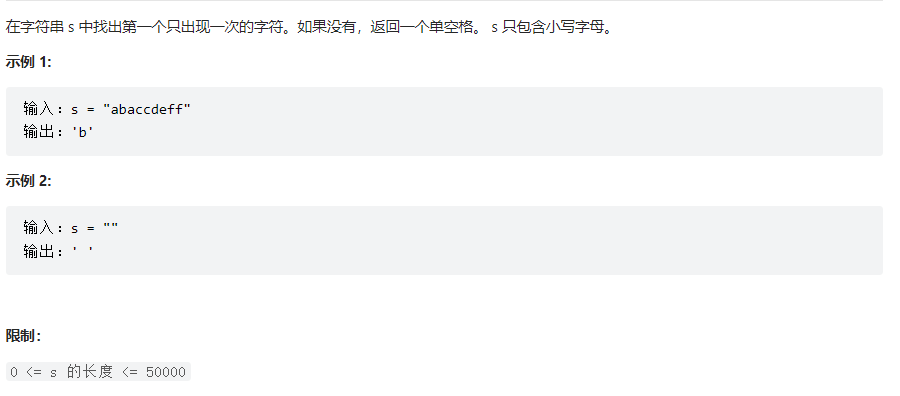
思路
哈希表
用哈希表构建字符是否是出现了一次
有序哈希表
用有序哈希表构建字符是否是出现了一次
代码实现
哈希表
class Solution {
HashMap<Character,Boolean> map=new HashMap<Character,Boolean>();
public char firstUniqChar(String s) {
char[] chars= s.toCharArray();
for(char c:chars){
map.put(c,!map.containsKey(c));
}
for(char c:chars){
if(map.get(c)){
return c;
}
}
return ' ';
}
}
有序哈希表
class Solution {
LinkedHashMap<Character,Boolean> map=new LinkedHashMap<Character,Boolean>();
public char firstUniqChar(String s) {
char[] chars= s.toCharArray();
for(char c:chars){
map.put(c,!map.containsKey(c));
}
for(Map.Entry<Character,Boolean> entry:map.entrySet()){
if(entry.getValue()){
return entry.getKey();
}
}
return ' ';
}
}
复杂度分析
时间复杂度
均为O(N),但是后者第二遍遍历次数少,字符串越长后者优势越大
空间复杂度
均为O(N)
反思不足
思路
最开始想的是set集合配合哈希表,添加成功时,就把元素加入哈希表中,反之则删除,的确可以达成目的,但是没必要,直接用哈
希表对应其是不是只出现了一次不就完了嘛
可见模式识别不是那么容易用的,不小心还会思维固化
javase
Set有关
add方法添加元素
泛型不能是基本数据类型,Character对应char
Map有关
HashMap无序,插入顺序不代表输出顺序
LinkedHashMap则是有序的
put添加基本元素
remove根据键删除
values获取所有值,而后toArray可以转化成Object数组
size获取键值对数量
containsKey判断是否存在对应键
entrySet返回所有键值对,用Map.Entry<E,E>接收,getValue,getKey
泛型不能是基本数据类型,Character对应char
泛型建议两边都写上,影响返回值类型



