从尾到头打印链表
题目要求

思路
逆置法
将链表逆置再打印即可,注意,返回值不计入空间复杂度!!!
辅助栈法
利用栈的先进后出特性,顺序遍历链表并将指入栈,然后将栈的元素给数组即可
数组法
由于数组可随机存取,故可以得到链表的长度后申请一个数组然后再顺序遍历链表并将值从数组后往前插入。
代码
逆置法
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {
//逆置总得保存前指针吧?因为是单向链表。
ListNode pre=null,cur=head;
//记录链表长度
int cth=0;
while(cur!=null){
//总得保存当前节点后的节点吧,不然改变当前节点的next域后就丢失了
ListNode next=cur.next;
cur.next=pre;
pre=cur;
cur=next;
cth++;
}
int[] result=new int[cth];
for(int i=0;i<cth&&pre!=null;i++){
result[i]=pre.val;
pre=pre.next;
}
return result;
}
}
辅助栈法
数组法
复杂度分析
时间复杂度
逆置法均为O(n)
空间复杂度
逆置法、数组法为O(1),注意返回值不计入空间复杂度。
辅助栈法为O(n)
反思不足
思路
最开始没有考虑这是不是有头节点的链表,采用了头插法做。
对头插法、原地逆置法这两个逆置方法不熟悉。
反转链表
题目要求

思路
迭代
迭代算法的基本思想是:为求一个问题的解x,可由给定的一个初值x0,根据某一迭代公式得到一个新的值x1,这个新值x1比初值x0更接近要求的值x;再以新值作为初值,即:x1→x0,重新按原来的方法求x1,重复这一过程直到|x1-x0|<ε(某一给定的精度)。此时可将x1作为问题的解x。
利用迭代算法解决问题,需要做好以下三个方面的工作:
(1)确定迭代变量。在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值推出新值的变量,这个变量就是迭代变量。
(2)建立迭代关系式。所谓迭代关系式(即重复进行的操作),指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键。
(3)对迭代过程进行控制。在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。
迭代也是用循环结构实现,只不过要重复的操作是不断从一个变量的旧值出发计算它的新值。其基本格式描述如下:
迭代变量赋初值;
while (迭代终止条件)
{
根据迭代表达式,由旧值计算出新值;
新值取代旧值,为下一次迭代做准备;
}
初次接触迭代这个概念,个人理解应该是由部分到整体的过程,先在局部实现目标,然后在其基础上实现后续目标。
头插法
随着遍历的的进行,让当前节点的next域指向头节点的next域,然后更新头节点的next域为当前节点,注意要存储当前节点的下一节点并且时候将当前节点更新为下一节点,循环直到当前节点为null。
原地逆置
用一个指针pre记录上一个节点,一个指针cur记录当前节点,一个指针next记录当前节点的下一节点,将当前节点的next域指向pre,而后更新当前节点为next。
递归
将问题分解为若干个用同样的方法解决的小问题,以此实现用同样的方法处理不同规模的问题。
使用时要确定递归终止的条件,终止时的操作,以及相同的处理方法。
递归至最后一个节点,将其作为头节点返回,除最底层调用外,每一层调用都要将当前节点的next域指向前一个节点或者将下一个节点的next域指向当前节点,并将当前节点next域指向null。
代码
迭代
头插法
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode h=new ListNode(),cur=head;
h.next=null;
while(cur!=null){
ListNode next=cur.next;
cur.next=h.next;
h.next=cur;
cur=next;
}
//链表原设定无头节点,不能返回头节点
return h.next;
}
}
原地逆置
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre=null,cur=head;
//记录链表长度
while(cur!=null){
//总得保存当前节点后的节点吧,不然改变当前节点的next域后就丢失了
ListNode next=cur.next;
cur.next=pre;
pre=cur;
cur=next;
}
return pre;
}
}
递归
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null||head.next==null){//前一个条件是为了防止传进来一个空链表
return head;
}
ListNode h=reverseList(head.next);
head.next.next=head;
head.next=null;
}
}
复杂度分析
空间复杂度
迭代均为O(1)
递归为O(n)
时间复杂度
均为O(n)
反思不足
思路
对迭代这种方法的使用不熟悉,算是初次在算法里听说这个概念。
并不知道链表的翻转还可以用递归做,同样,算是初次正儿八经的接触算法中的递归。
复杂链表的复制
题目要求
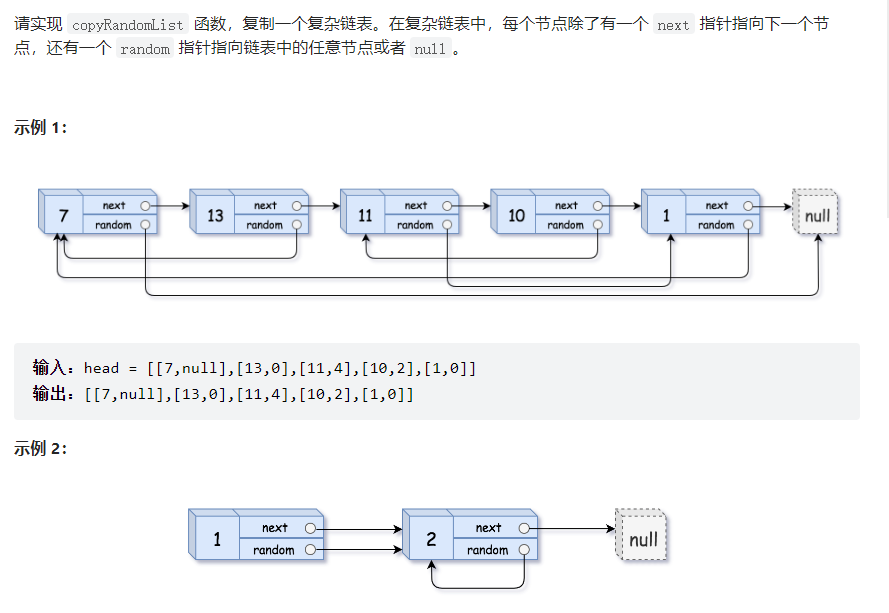
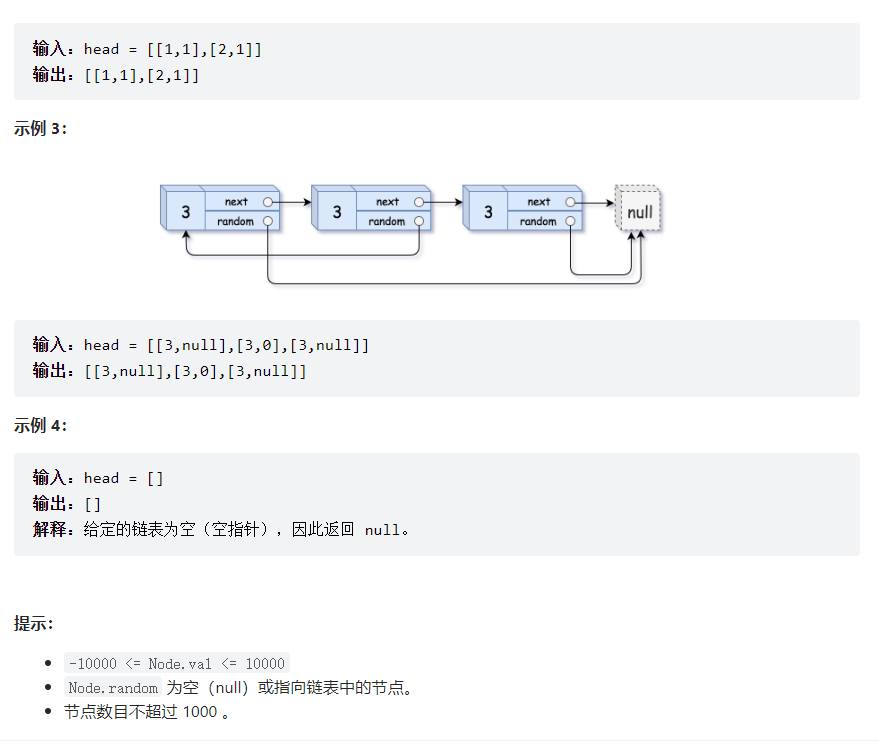
思路
迭代+哈希表
题目特征
注意到本题每个节点的处理方法都相同,拷贝值,建立next域联系和random域联系,于是想到可以用迭代。
哈希表
一个可以通过键快速获取值的数据结构。
本题中因为要频繁的获取每个节点的复制节点,所以使用到了哈希表。
本题的难点在于random指针指向节点的随机性,不像next那样可以很方便的直接取到。
于是我们通过哈希表的方式,先建立原节点与复制节点间的映射关系,不去管next域和random域,可以很方便的确定原节点对应的复制节点后再去构建next域和random域就会很容易。
回溯+哈希表
回溯
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。——百度百科
使用这种算法尤其要注意回溯点。
但是本题为什么要用回溯法呢?有什么好处呢?
可能只是解题思路的不同吧
迭代+节点拆分
这种思路采用了另一种方法来建立原节点与复制节点的映射,将原节点的next域指向复制节点,复制节点的next域指向原节点的下一个节点。同样可以快速确定原节点对应的复制节点。并且还节省了哈希表的空间
最后要拆分出来,需要三个辅助指针。
代码
迭代+哈希表
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
HashMap<Node,Node> hashMap=new HashMap<Node,Node>();
public Node copyRandomList(Node head) {
Node cur=head;
while(cur!=null){
Node node=new Node(cur.val);
hashMap.put(cur,node);
cur=cur.next;
}
cur=head;
while(cur!=null){
hashMap.get(cur).next=hashMap.get(cur.next);
hashMap.get(cur).random=hashMap.get(cur.random);
cur=cur.next;
}
return hashMap.get(head);
}
}
回溯+哈希表
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
HashMap<Node,Node> hashMap=new HashMap<Node,Node>();
public Node copyRandomList(Node head) {
if(head==null){
return null;
}
if(!hashMap.containsKey(head)){
Node newHead=new Node(head.val);
hashMap.put(head,newHead);
hashMap.get(head).next=copyRandomList(head.next);
hashMap.get(head).random=copyRandomList(head.random);
}
return hashMap.get(head);
}
}
迭代+节点拆分
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
public Node copyRandomList(Node head) {
if(head==null){
return null;
}
Node cur=head;
while(cur!=null){
Node newNode= new Node(cur.val);
newNode.next=cur.next;
cur.next=newNode;
cur=newNode.next;
}
cur=head;
while(cur!=null){
Node newNode=cur.next;
Node next=newNode.next;
newNode.random=cur.random!=null?cur.random.next:null;
cur=next;
}
cur=head;
Node newHead=head.next;
while(cur!=null){
//当前节点的复制节点
Node newNode= cur.next;
//当前节点的下一个原节点
Node next=newNode.next;
newNode.next=next!=null?newNode.next.next:null;
cur.next=next;
cur=next;
}
return newHead;
}
}
复杂度分析
空间复杂度
迭代/回溯+哈希表均为O(n),但要注意回溯还有个递归。
迭代+节点拆分为O(1),注意返回值不计入。
时间复杂度
迭代/回溯+哈希表均为O(n),迭代源于两次对链表的遍历,回溯的话,每个节点会访问next和random各一次,均摊为两次
迭代+节点拆分也为O(n),源于三次遍历链表。
反思不足
思路
最开始不知道要深拷贝,于是以为问题很简单。
发现需要深拷贝后就束手无策了。
但是仔细想想,此时遇到的问题是什么,是需要用到的节点没有建立,那怎么办,预先建立不久完了,而后就是怎么对应的问题了,学过哈希表后可以想到用哈希表
但当时确确实实就是卡住了,没有想着去解决这个问题。
后来实现题解思路时,没有去考虑当传入链表为空时该怎么办。
在拆分时,最开始的思路是两个关系同时来,没有顾及到next的改变会影响到random的建立,要考虑系统间的互相影响。
java se
对HashMap的有关API不太熟悉
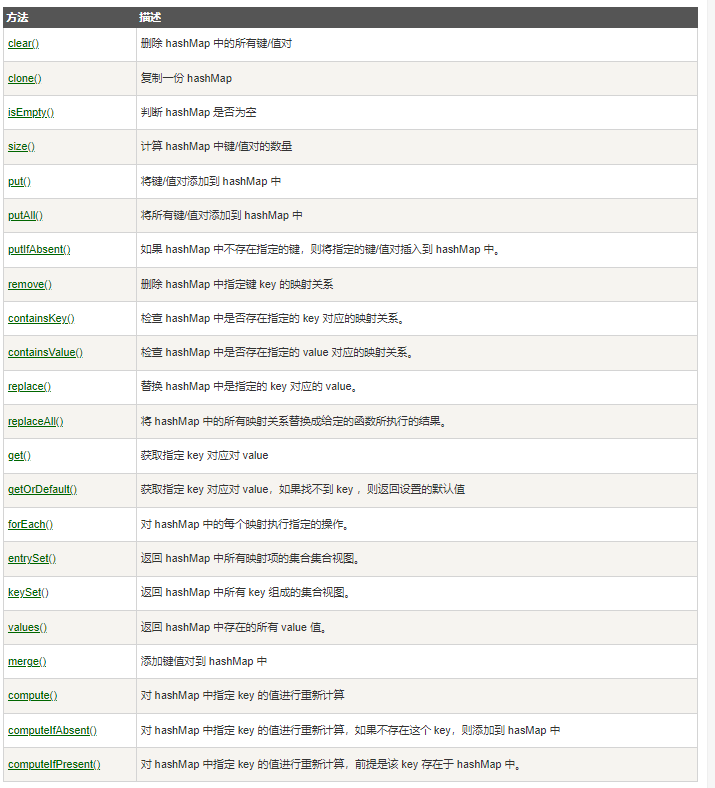
审题
一般设计到复制的大概率是深拷贝,尤其有指针的话
深拷贝是指源对象与拷贝对象互相独立,其中任何一个对象的改动都不会对另外一个对象造成影响。
一般是不能对传入参数的内容进行修改的,所以节点拆分时要注意还原回原来的样子



