CF1292D Chaotic V.

链接:https://www.luogu.com.cn/problem/CF1292D

话说这个题怎么比上面那道题还要简单，顺序是不是弄反了。

讲一讲我的做法:

题解:如果我们把这些数看成一棵树，每个节点x的父亲是\(\frac{x}{f(x)}\)(其中\(f(x)\)是\(x\)的最小质因子)。样例的图给了我们一个很好的示范:

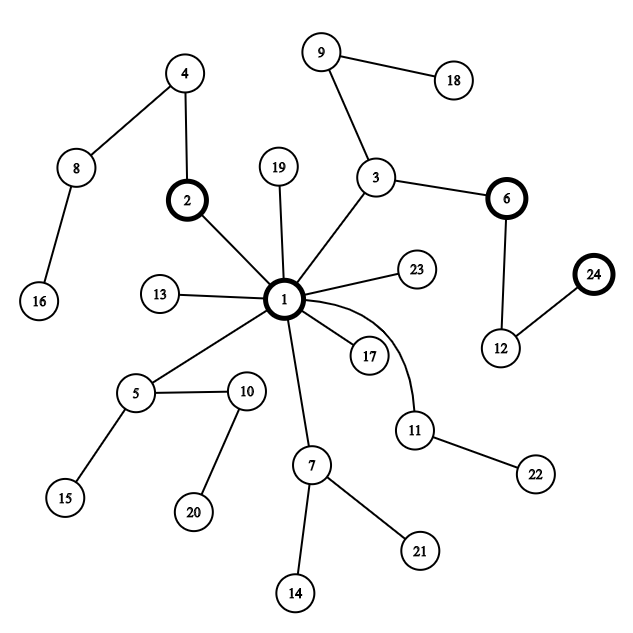
我们可以发现，原问题其实就是让我们求一个节点到所有结点的路径和最小，其实这就是一个树上问题。

我们考虑解决这个树上问题，由于数太大，我们可以做一个类似扩域的操作，定义树上的每一个数都为(\(a_{1},a_{2},a_{3},...a_{5000}\))的形式(其中\(a_{i}\)表示在该数的质因子中，\(i\)出现的次数)。

现在我们需要定义如下三个运算：

\(1.x\times y\)

\(2.lca(x,y)\)

\(3.dis(x,y)\)

对于第一种运算，将每一位的\(a_{i}\)相加即可。我们可以用第一种运算预处理\(x!\)所表示的数。

对于第二种运算，可以求出两个数的最长公共后缀，最长公共后缀的位就取它们两个相同的值，不一样的那一位取最小值，前面的位就取\(0\)。

对于第三种运算，也可以求出两个数的最长公共后缀，最长公共后缀的位没有贡献，不一样的那一位的贡献则为它们的差，前面的位的贡献则为它们的和。

考虑树上的节点过多，而有用的只有输入的节点以及它们的\(lca\)，所以我们可以重新建一棵树。由于一个\(lca\)可能是另外两个\(lca\)的\(lca\)，而深度最大的\(lca\)不能是其他\(lca\)的\(lca\)。所以我们可以将\(lca\)按深度排序，利用类似\(kruskal\)重构树的方法建树。但这样的\(lca\)有\(n^2\)个，建树的复杂度过高。

考虑优化。重新考虑第二种运算，可以发现每个数的\(lca\)的深度即为两个数的最长公共后缀的大小。将每个数看作一个字符串，因为质因子个数是递增的，所以较小数的字典序也最小。利用后缀数组的值是我们知道，字典序相邻的最长公共后缀会尽量大，所以我们使用到的\(lca\)只有相邻两数的\(lca\)。

建出树后，原问题彻彻底底的变为了树上问题，换根\(dp\)即可。

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
struct node
{
	int map[5001];
};
struct reads
{
	int v,data,nxt;
};
reads edge[10001];
node a[10001],sum[10001];
int b[1000001],n,x,leng;
long long S,head[10001],len,dp[10001],dp2[10001],sz[10001],res=1e18,t,num[10001],length;
bool used[10001];
node c,ans;
struct tree_made
{
	int depth,num,x,y;
	bool operator < (const tree_made &t)const
	{
		return depth>t.depth;
	}
};
tree_made LCA[5001];
void add_edge(int x,int y,int z)
{
	edge[++len].v=y;
	edge[len].data=z;
	edge[len].nxt=head[x];
	head[x]=len;
	return;
}
node add(node a,node b)
{
	for (int i=1;i<=5000;++i)
		c.map[i]=a.map[i]+b.map[i];
	return c;
}
int dist(node a,node b)
{
	int sum=0,i;
	for (i=5000;i>=1;--i)
		if (a.map[i]!=b.map[i])
		{
			sum=abs(a.map[i]-b.map[i]);
			break;
		}
	i--;
    for (;i>=1;--i)
    	sum+=a.map[i]+b.map[i];
    return sum;
}
node lca(node a,node b)
{
	for (int i=1;i<=5000;++i)
		c.map[i]=0;
	for (int i=5000;i>=1;--i)
	{
		c.map[i]=a.map[i];
		if (a.map[i]!=b.map[i])
		{
			c.map[i]=min(a.map[i],b.map[i]);
			return c;
		}
	}
	return a;
}
void dfs(int x)
{
	used[x]=1;
	dp[x]=0;
	sz[x]=num[x];
	for (int i=head[x];i>0;i=edge[i].nxt)
		if (!used[edge[i].v])
		{
			dfs(edge[i].v);
			dp[x]+=dp[edge[i].v]+sz[edge[i].v]*edge[i].data;
			sz[x]+=sz[edge[i].v];
		}
	return;
}
void dfs2(int x)
{
	used[x]=0;
	for (int i=head[x];i>0;i=edge[i].nxt)
		if (used[edge[i].v])
		{
			dp2[edge[i].v]=dp2[x]+edge[i].data*(n-sz[edge[i].v])-sz[edge[i].v]*edge[i].data;
			dfs2(edge[i].v);
		}
	return;
}
int rt[10001];
int find(int x)
{
	if (rt[x]==x)
		return x;
	return rt[x]=find(rt[x]);
}
void unionn(int x,int y)
{
	rt[find(x)]=find(y);
	return;
}
signed main()
{
	cin>>n;
	for (int i=2;i<=5000;++i)
	{
		t=i;
		for (int j=2;j*j<=i;++j)
			if (t%j==0)
			{
				while (t%j==0)
				{
					t/=j;
					a[i].map[j]++;
				}
			}
		if (t>1)
			a[i].map[t]++;
	} 
	for (int i=1;i<=5000;++i)
		sum[i]=add(sum[i-1],a[i]);
	for (int i=1;i<=n;++i)
		cin>>b[i];
	for (int i=1;i<=n;++i)
	{
		if (b[i]==0)
			b[i]++;
		num[b[i]]++;
	}
	for (int i=1;i<=10000;++i)
		rt[i]=i;
	length=0;
	S=5000;
	for (int i=2;i<=5000;++i)
	{
		if (dist(lca(sum[i],sum[i-1]),sum[i-1])!=0)
		{
			++S; 
			LCA[++length].num=S;
			sum[S]=lca(sum[i],sum[i-1]);
		}
		else
			LCA[++length].num=i-1;
		LCA[length].x=i;
		LCA[length].y=i-1;
		LCA[length].depth=dist(sum[1],lca(sum[i],sum[i-1]));
	}
	sort(LCA+1,LCA+length+1);
	for (int i=1;i<=length;++i)
	{
		add_edge(LCA[i].num,find(LCA[i].x),dist(sum[LCA[i].num],sum[find(LCA[i].x)]));
		add_edge(LCA[i].num,find(LCA[i].y),dist(sum[LCA[i].num],sum[find(LCA[i].y)]));
		if (find(LCA[i].x!=LCA[i].num))
			unionn(LCA[i].x,LCA[i].num);
		if (find(LCA[i].y!=LCA[i].num))
			unionn(LCA[i].y,LCA[i].num);
	}
	dfs(LCA[length].num); 
	dp2[LCA[length].num]=dp[LCA[length].num];
	dfs2(LCA[length].num);
	for (int i=1;i<=S;++i)
		res=min(res,dp2[i]);
	cout<<res<<endl;
	return 0;
}