# Solving PDEs on Spheres with PICNN report_1
1. 引言
- 受限于计算效率,数值求解PDE的经典方法(有限差分,有限元,无网格)在高维情况下不再适用. 近年来,利用深度神经网络求解高维偏微分方程已经有了广泛的研究,如Deep Ritz methods( DRMs ),Physics-Informed Neural Networks( PINNs ) ,Neural Operators和DeepONets. DRMs和PINNs利用神经网络强大的逼近能力直接学习PDEs的解,相比之下,Neural Operators和DeepONets专门学习将初始条件或边界条件映射到求解函数的算子.
- 在本文重点研究了PINN方法. 先前的研究主要涉及在欧氏空间上的physical domain使用全连接神经网络结构对PINNs的泛化界进行收敛性分析,这距离我们的目标:使用CNN结构来进行分析还是有一定差距。此外,解流形上的PDE对于实际应用具有很大价值,这使得流形学习成为机器学习中一个充满活力的领域. 低本征数据维度已经被证实可以有效地屏蔽来自维数灾难的学习算法。尽管已有一些关于流形上PDEs的PINN框架的探索,但仍然缺乏全面的收敛性分析.
- 本研究是为解决这一差距所做的开创性工作. 本文提出将具有CNN结构的PINNs应用于求解单位球面上的一般s阶PDEs,同时建立此类PDE求解器的收敛性分析:通过使用球谐分析来探索CNNs的逼近潜力(bound approximation error),评估模型的Rademacher复杂度(bound statistical error),并通过各种技术估计得出优雅的泛化边界.
2. 预备:问题描述 合适假设
2.1. PINN for General PDEs
对于一般的PDE,有以下的边值问题.
\[\begin{cases}
(\mathcal{L}u)(x) = f(x)& , x \in \Omega \subset \mathbb{R}^d \\
u(x) = g(x)& ,x \in \partial\Omega
\end{cases}\]
此处 \(\mathcal{L}\) 是一般的微分算子,\(\Omega\) 是有界区域.
PINN将此问题转化为优化问题,目标函数有以下形式:
\[\mathcal{R}(u) = \frac{1}{vol(\Omega)}\int_\Omega |(\mathcal{L}u)(x) - f(x)|^2 \mathrm{d}x +\frac{1}{\sigma(\partial\Omega)}\int_{\partial\Omega}|u(x) - g(x)|^2\mathrm{d}\sigma
(x)
\]
这里的 \(\sigma\) 是 \(\partial\Omega\) 上的均匀测度.
为了方便计算,我们有以下empirical version:
\[\mathcal{R}_{n,m}(u) = \frac{1}{n} \sum_{i=1}^{n}|(\mathcal{L}u)(X_i) - f(X_i)|^2 + \frac{1}{m}\sum_{i=1}^{m}|u(Y_i) - g(Y_i)|^2
\]
其中\(\{X_i\}_{i=1}^n\sim Unif(\Omega),i.i.d.\) 且 \(\{Y_i\}_{i=1}^m\sim Unif(\partial\Omega),i.i.d.\).
PINN解决Empirical Risk Minimization(ERM)问题
\[u_{n,m} = \argmin_{u \in \mathcal{F}} \mathcal{R}_{n,m}(u)
\]
这里的\(\mathcal{F}\)是我们预先定义好的函数空间(假设空间).
2.2. 量化指标
2.2.1. 算法视角
ERM算法的效果由excess risk来衡量:\(\mathcal{R}(u_{n,m})-\mathcal{R}(u^*)\)
我们将excess risk的衰减速率成为算法的convergence rate或者是learning rate. 它是衡量算法效能的重要指标. 本文则是证明了PICNN算法给出了\(n^{-a}(\log n)^{2a}\)的收敛速度,其中\(a\)是一个与维度 \(d\),方程本身阶数 \(s\) 和对应索伯列夫空间 \(H^s\)有关的一个常数.
2.2.2. PDE视角
从函数逼近的视角来看,我们可以用\(||u_{n,m} - u^*||\)来衡量解的精确性,其中范数是在一个正则空间上定义的,比如索伯列夫空间.
这就引出一个很重要的问题,这两种指标是否等价?也就是说,能否用 \(\mathcal{R}(u_{n,m})-\mathcal{R}(u^*)\) 去 bound \(||u_{n,m} - u^*||\),或者反过来用\(||u_{n,m} - u^*||\) 来bound \(\mathcal{R}(u_{n,m})-\mathcal{R}(u^*)\).当两种指标等价时,我们称算法满足 strong convexity of PINN risk w.r.t. \(W_p^r(\Omega)\) norm. 我们会用一个例子表明这种性质是不平凡的.
例子 考虑线性PDE,即 \(\mathcal{L}\) 是线性算子,有:
\[\begin{aligned}
\mathcal{R}(u) - \mathcal{R}(u^*) &=\frac{1}{vol(\Omega)}\int_\Omega |(\mathcal{L}u)(x) - f(x)|^2 \mathrm{d}x +\frac{1}{\sigma(\partial\Omega)}\int_{\partial\Omega}|u(x) - g(x)|^2\mathrm{d}\sigma \\
&= \frac{1}{vol(\Omega)}\int_\Omega |\mathcal{L}(u-u^*)(x) |^2 \mathrm{d}x +\frac{1}{\sigma(\partial\Omega)}\int_{\partial\Omega}|u(x) - u^*(x)|^2\mathrm{d}\sigma\\
&=\frac{1}{vol(\Omega)}||\mathcal{L}(u-u^*)||^2_{L^2(\Omega)} + \frac{1}{\sigma(\partial\Omega)}||u-u^*||^2_{L^2({\partial}\Omega)}
\end{aligned}
\]
首先考虑用 \(\mathcal{R}(u) - \mathcal{R}(u^*)\) 控制 \(||u-u^*||_{W_p^r(\Omega)}\),对于 \(2s\) 阶的微分算子 \(\mathcal{L}\) 我们给出下面几个先验估计.
![Alt text]()
这里我们主要使用(2.3),得到下式
\[||u-u^*||_{H^{2s}(\Omega)} \lesssim||\mathcal{L}(u-u^*)||_{L^2({\Omega})} + ||u-u^*||_{H^{\frac{2s-1}{2}}(\partial\Omega)}
\]
可以看到在边界项上产生差异,解决办法有考虑硬约束形式:
\[u(x) = g(x) , \quad x \in \partial\Omega , u \in \mathcal{F}
\]
则
\[||u-u^*||_{H^{2s}(\Omega)} \lesssim||\mathcal{L}(u-u^*)||_{L^2({\Omega})} \quad for \quad u \in \mathcal{F} \cap H^{2s}(\Omega)
\]
本文考虑的是球面,不存在边界,因此也不需要考虑边界项.
用 \(||u-u^*||_{W_p^r(\Omega)}\) 控制 \(\mathcal{R}(u) - \mathcal{R}(u^*)\) 是直接的计算
\[\begin{aligned}
\mathcal{R}(u) - \mathcal{R}(u^*) \lesssim&||\mathcal{L}(u-u^*)||^2_{L^2(\Omega)} + ||u-u^*||^2_{L^2({\partial}\Omega)} \\
\lesssim&||u-u^*||_{H^{2s}(\Omega)}+ ||u-u^*||^2_{L^2({\partial}\Omega)}
\end{aligned}
\]
这里我们假设 \(\mathcal{L}\) 是 \(s\) 阶的线性微分算子.
至此我们已经看出strong convexity不是一个平凡的性质,尤其针对索伯列夫范数的情况. 另外一个重要的考虑是PDE解的唯一性,此时PINN可能会出现问题,但本文没有讨论适定问题.
2.3. PINN for PDEs on Spheres
考虑球面上的PDE,就是要将欧氏空间的导数和范数(索伯列夫)的形式搬到球面上来.
定义: Laplace_Beltrami operator \(\triangle_{0}\)
\[\triangle = \frac{\partial ^{2}}{\partial \rho^{2}} + \frac{(d-1)}{\rho} \frac{\partial }{\partial \rho} + \frac{1}{\rho^{2}}\triangle_{0}
\]
由 \(\frac{\partial }{\partial \rho} = \frac{1}{\rho}\sum_{i=1}^{d}x_i\frac{\partial }{\partial x_i}\) 得到
\[\triangle_{0} = \sum_{i=1}^{d}\frac{\partial ^{2}}{\partial x_i^{2}} - \sum_{i=1}^{d}\sum_{j=1}^{d}x_ix_j\frac{\partial ^{2}}{\partial x_i \partial x_j} - (d-1)\sum_{i=1}^{d}x_i\frac{\partial }{\partial x_i}
\]
球面上的索伯列夫范数 \(||\cdot||_{W^{r}_{p}(\mathbb{S}^{n-1})}\) 定义如下
定义:
\[||f||_{W^{r}_{p}(\mathbb{S}^{n-1})} = ||f||_{p} + \sum_{1\leq i <j \leq d} ||D_{i,j}^{r}f||_{p}
\]
其中角导数 \(D_{i,j}^{r}\) 定义如下
\[D_{i,j}^{r} = x_i\frac{\partial }{\partial x_j}-x_j\frac{\partial }{\partial x_i}
\]
结合角导数,L-B算子有以下形式
\[\triangle_0 = \sum_{1\leq i <j \leq d}D_{i,j}^{2}
\]
PDE变为
\[(\mathcal{L}u)(x) = f(x), \quad x\in \mathbb{S}^{d-1},\quad d\ge 3
\]
risk函数也变为球面上的形式
\[\mathcal{R}(u) = \frac{1}{\omega_{d}}\int_{\mathbb{S}^{d-1}}|(\mathcal{L}u)(x)-f(x)|^{2}\mathrm{d}\sigma(x)
\]
\[\mathcal{R}_{n}(u) = \frac{1}{n} \sum_{i=1}^{n}|(\mathcal{L}u)(X_i) - f(X_i)|^2
\]
\(\{X_i\}_{i=1}^n\sim Unif(\mathbb{S}^{d-1}),i.i.d.\)
ERM:
\[u_n = \argmin_{u \in \mathcal{F}} \mathcal{R}_{n}(u)
\]
2.4. 定理假设
基于上述前提,我们就可以提出相应的假设
本文没有讨论适定性问题,但假设 \(u^*\)是唯一解仍是必需的. 对 \(u^*\) 的正则性也需要做出假设,因为 risk 是针对范数 \(H^s\),我们的分析需要假设 \(u^*\)具有更高的正则性,也即 \(u^* \in H^{r}(\mathbb{S}^{d-1})\),对 $ r \ge s+1$,基于椭圆正则性定理,我们有
\[u^* \in H^{-\infty}(\mathbb{S})^{d-1},f \in H^t(\mathbb{S}^{d-1}) \Rightarrow u^* \in H^{t+s}(\mathbb{S}^{d-1})
\]
所以假设 \(f \in H^{r-s}(\mathbb{S}^{d-1})\)就可以(但是在后面的假设1里没有提到 \(f\)).
但是,如果要使用Bernstein inequality 或 talagrand inequality,我们还需要有界性假设,我们的分析表明只需要假设 \(u^* \in W^{r}_{\infty}(\mathbb{S}^{d-1})\),总的来说,要做出如下假设
2.4.1. 假设 1
假设 \(\mathcal{L}\)是一个 \(s \in \mathbb{N}\) 阶的线性微分算子,有如下形式
\[\mathcal{L} = \sum_{|\alpha|\le s} a_\alpha(x)D^{\alpha},
\]
这里 \(\alpha = (\alpha_1,\alpha_2,\alpha_3,\dots,\alpha_n )\) 是重指标,\(a_{\alpha}(\cdot) \in L^{\infty}(\mathbb{S}^{d-1})\).
假设方程有唯一解 \(u^* \in W^{r}_{\infty}(\mathbb{S}^{d-1})\) 对某个 \(r \ge s+1\),进一步,假设有如下估计
\[||u-u^*||_{H^{s}(\mathbb{S}^{d-1})} \lesssim||\mathcal{L}(u-u^*)||_{L^2(\mathbb{S}^{d-1})}
\]
值得注意的是在假设1中,我们假设算子 \(\mathcal{L}\) 是线性的.线性假设主要是为了阐述与 PINN 的strong convexity. 然而,这一性质在收敛性分析中几乎没有被使用。因此,考虑一个非线性算子是可行的,但这时候验证系数的无穷范数有界条件就会变得十分困难.
我们通过两个例子解释假设1起到的作用
例 1 static Schrodinger equation
\[-\triangle_0 u(x) + V(x)u(x) = f(x), \quad x \in \mathbb{S}^{d-1}
\]
注意到 $\triangle_0 $ 是一个特征值 \(\lambda \le 0\)的自伴算子,故如果 \(V\)是一个严格正常数函数,则方程有唯一解 \(u^*\),根据正则性定理
\[u^* \in H^{r}(\mathbb{S}^{d-1}) \Longleftrightarrow f \in H^{r-2}(\mathbb{S}^{d-1})
\]
此时可以验证 PINN risk 的 strong convexity 性质:
\[\begin{aligned}
\mathcal{R}(u) - \mathcal{R}(u^*) &= \frac{1}{\omega_d}\int_{\mathbb{S}^{d-1}}|\triangle_0 u(x) - Vu(x) + f(x)|^2 \mathrm{d}\sigma(x) \\
&=\frac{1}{\omega_d}\int_{\mathbb{S}^{d-1}}|\triangle_0 u(x) - Vu(x)- \triangle_0u^*(x)+ Vu^*(x)|^2 \mathrm{d}\sigma(x)\\
&=\frac{1}{\omega_d}\int_{\mathbb{S}^{d-1}}(\triangle_0 u- \triangle_0u^*)^2+ (Vu-Vu^*)^2 -2(\triangle_0u-\triangle_0u^*) \cdot (Vu-Vu^*) \mathrm{d}\sigma\\
&=\frac{1}{\omega_d}\int_{\mathbb{S}^{d-1}}(\triangle_0 u- \triangle_0u^*)^2+ V^2(u-u^*)^2 -2V||\nabla_0(u-u^*)||^2 \mathrm{d}\sigma
\end{aligned}
\]
这里 \(\nabla_0\) 是 \(\mathbb{S}^{d-1}\) 的投影梯度算子
因此我们有
\[\frac{\min\{ 1,V^2,2V \}}{\omega_d}||u-u^*||^2_{H^2(\mathbb{S}^{d-1})} \le \mathcal{R}(u) -\mathcal{R}(u^*) \leq \frac{\max\{ 1,V^2,2V \}}{\omega_d}||u-u^*||^2_{H^2(\mathbb{S}^{d-1})}
\]
例 2 考虑 \(2s\)阶椭圆方程
\[(-\triangle_0 +\lambda I)^{s}u(x) = f(x), \quad x \in \mathbb{S}^{d-1}
\]
这里 \(\lambda > 0\),同样的可以验证 PINN 的 strong convexity. 索伯列夫空间 \(W^{r}_{p}(\mathbb{S}^{d-1})\) 的另一个定义有如下形式.
\[||u||_{W^{r}_{p}(\mathbb{S}^{d-1})} = ||(-\triangle_0+I)^{r/2}u||_p
\]
在此范数下,\(r \in \mathbb{R}\),通过球谐展开在分布意义下定义分数阶幂。因此,这个方程内在地服从正则性定理,使得
\[u \in W^{r}_{p}(\mathbb{S}^{d-1}) \Longleftrightarrow f \in W^{r-2s}_{p}(\mathbb{S}^{d-1})
\]
注:右边到左边就是正则性定理的内容,左边到右边需要观察到
\[(-\triangle_0+I)^{r/2}u = (-\triangle_0+I)^{r/2-s}f \in L^P(\mathbb{S}^{d-1})
\]
所以在假设1中设置 \(f \in W^{r-2s}_{\infty}(\mathbb{S}^{d-1})\) 是等价的.
2.4.2. CNN 结构
总的来说,本文考虑的网络结构如下所示
首先是L层卷积网:
\[F^{(0)}: \mathbb{R}^{d} \to \mathbb{R}^{d}, \quad F^{(0)}(x) = x;
\]
\[F^{(l)}: \mathbb{R}^{d}\to \mathbb{R}^{d}, \quad F^{(l)}(x) = \sigma^{(l)} \left( \left( \sum_{j=1}^{d_l-1}w^{(l)}_{i-j}\left(F^{(l-1)}(x)\right)_j\right)_{i=1}^{d_l} -b^{(l)}\right)
\]
卷积操作可以写成下面乘卷积矩阵的形式(深度卷积神经网络可以看作是全连接深度神经网络的一种特殊稀疏形式):
\[ \left( \sum_{j=1}^{d_l-1}w^{(l)}_{i-j}\left(F^{(l-1)}(x)\right)_j\right)_{i=1}^{d_l} =T^{(l)}F^{(l-1)}(x)
\]
其中 \(T^{(l)}\)为 \(d_{l}\times d_{l-1}\)矩阵定义如下:
\[\begin{bmatrix}
w_{0}^{(l)}& 0 & 0 & 0&\cdots&0 \\
w_{1}^{(l)} & w_{0}^{(l)} & 0 & 0&\cdots&0 \\
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\
w_{S^{(l)}-1}^{(l)} & \cdots & w_{0}^{(l)} & 0&\cdots&0 \\
\vdots&\vdots&\vdots&\vdots&\vdots\vdots&\\0&\cdots&0&w^{(l)}_{S^{(l)}-1}&\cdots&w^{(l)}_0\\
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\\0&0&0&\cdots&0&w^{(l)}_{S^{(l)}-1}
\end{bmatrix}
\]
这里,激活函数 \(\sigma(x)\)是 ReLU 函数,\(\{ w^{(l)} \}_{l=1}^{L}\)为卷积核,\(w^{(l)}: \mathbb{Z} \to \mathbb{R}\) 代表下标为 \(\mathbb{Z}\),支撑集在 \(\{ 0, \ldots ,S^{(l)}-1 \}\),给定 kernel size \(S^{(l)}\ge 3\),\(b^{(l)} \in \mathbb{R}^{d_l}\)是残差向量,网络宽度 \(d_{0}=d, \{ d_{l}=d_{l-1}+S^{(l)}-1 \}_{l=1}^{L}\)
在第 L 层,我们引进池化降维操作:\(\mathcal{D}: \mathbb{R}^{d_L}\to \mathbb{R}^{[d_{L}/d]}\) 定义为 \(\mathcal{D}(x) = (x_{id})_{i=1}^{[d_{L}/d]}\)
接下来是 \(L_{0}\)个全连接网络和最终输出层:
\[\begin{aligned}
F^{(L+1)}:&\mathbb{R}^{d}\to \mathbb{R}^{d_{L+1}} \\
&F^{L+1}(x)=\sigma^{(L+1)}\left( W^{(L+1)}\mathcal{D}\left( F^{(L)}(x)\right)-b^{(L+1)}\right);
\end{aligned}
\]
\[\begin{aligned}
F^{(l)}:&\mathbb{R}^{d}\to \mathbb{R}^{d_{l}} \\
&F^{l}(x)=\sigma^{(l)}\left( W^{(l)}F^{l-1}(x)-b^{(l+1)}\right), \quad l = L+2, \ldots ,L+L_0
\end{aligned}
\]
\[\begin{aligned}
F^{(L+L_0+1)}:&\mathbb{R}^{d}\to \mathbb{R} \\
&F^{L+L_0+1}(x)= W^{(L+L_0+1)}F^{L+L_0}(x)-b^{(L+L_0+1)};
\end{aligned}
\]
由于饱和现象(ReLU 函数的高阶导为0),本文考虑的是索伯列夫范数意义下的逼近,所以将部分 ReLU 函数光滑化,如 ReLU\(^k\),本文设置了 \(L_0 = 2\)且在全连接层使用ReLU\(^k\) 函数.
函数空间 \(\mathcal{F}\)由最终输出层定义,考虑到一些上确界范数的假设,我们把PICNN函数空间如下定义:
\[\begin{aligned}
\max_{l=1, \ldots ,L} ||w^{(l)}||_{\infty} \le B_{1} \\
\max_{l=1, \ldots ,L} ||b^{(l)}||_{\infty} \le B_{2} \\
\max_{l=L+1, \ldots ,L+L_0+1} ||W^{(l)}||_{\max} \le B_{3} \\
\max_{l=L+1, \ldots ,L+L_0+1} ||b^{(l)}||_{\infty} \le B_{4} \\
\end{aligned}
\]
此外,自由参数的数量 \(\mathcal{S}\)也定义了函数空间.另一个角度是将网络输出及其导数的上确界范数(限制在s阶),因此,我们选择\(M > 0\)来保证
\[\max_{|\alpha|\leq s}||D^{\alpha}F^{(L+L_0+1)}||_{\infty} \leq M \quad , F^{(L+L_0+1)} \text{限制在} \mathbb{S}^{d-1}
\]
我们将函数空间 \(\mathcal{F}\)描述如下
\[\begin{aligned}
&F(L,L_0,S,d_{L+1}, \ldots ,d_{L+L_0},\text{ReLU},\text{ReLU}^k,M,\mathcal{S}) \\
&= \left\{ F^{L+L_0+1}:\mathbb{S}^{d-1}\to \mathbb{R} |F^{(L+L_0+1)}\text{满足上面的要求},S^{(l)}=S,\sigma^{(l)}=\text{ReLU},l \neq L+1;\sigma^{(l)}= \text{ReLU}^k, l= L+1; K\geq s ;\text{自由参数的总数小于}\mathcal{S}\right\}
\end{aligned}
\]
2.4.3. 假设 2
函数空间 \(\mathcal{F}=F(L,L_0,S,d_{L+1}, \ldots ,d_{L+L_0},\text{ReLU},\text{ReLU}^k,M,\mathcal{S})\)如上述定义,其中,选择\(M\)充分大使得
\[\max_{|\alpha \leq s|}||D^{\alpha}u^*||_{\infty} \leq M
\]
此处,\(u^* \in W_{\infty}^{r}(\mathbb{S}^{d-1}),\quad r \geq s+1\),是方程的唯一解.
3. 主要结果
3.1. 定理 1
在假设 1 和假设 2 的基础上,令 \(d\geq 3\),\(x = \{ X_{i} \}_{i=1}^{n}\) 为$ i.i.d.$,取自单位球 \(\mathbb{S}^{d-1}\)的均匀分布. 令 $3\leq S\leq d \(,\)k$满足
\[\begin{cases} k = s+\left[ \frac{r+s+2}{d-3}\right], & if \quad r <\infty, d >3\\
k\ge s, & if\quad r<\infty,d=3 \quad or\quad r=\infty ,d \geq 3 \end{cases}
\]
\(u_n\) 为 PICNN 估计器,函数空间
\[F(L,L_0=2,S,d_{L+1}, d_{L+2},\text{ReLU},\text{ReLU}^k,M,\mathcal{S})
\]
其中
\[\begin{aligned}
L &\asymp n^{\frac{a(d-1)}{2(r-s)}}(\log n)^{-\frac{a (d-1)}{r-s}} \\
d_{L+1}&\asymp n^{\frac{a(d+r+s-1)}{2(r-s)(k-s+1)}+\frac{a(d+1)}{2(r-s)}}(\log n)^{-\frac{a(d+r+s-1)}{2(r-s)(k-s+1)}-\frac{a(d+1)}{r-s}}
\\
d_{L+2}&\asymp n^{\frac{a(d-1)}{2(r-s)}}(\log n)^{-\frac{a (d-1)}{r-s}}\\
\mathcal{S} &\asymp
\begin{cases}
n^{\frac{a(d-1)}{2(r-s)}}(\log n)^{-\frac{a (d-1)}{r-s}}, & if\quad r<\infty,d>3, \\
n^{\frac{a(d+r+s-1)}{2(r-s)(k-s+1)}+\frac{a}{r-s}}(\log n)^{-\frac{a(d+r+s-1)}{2(r-s)(k-s+1)}-\frac{2a}{r-s}}, & if\quad r<\infty,d=s \quad or \quad r=\infty,d\geq 3
\end{cases}
\end{aligned}
\]
常数 \(a\)
\[a=\begin{cases}
\frac{r-s}{(r-s)+(d-1)}, & for \quad r<\infty,d>3, \\
1-\frac{r+4k+6-3s}{2(r-s)(k-s+1)+r+4k=6-3s} , & for\quad r<\infty,d=3, \\
1-\frac{1}{2(k-s)+3} , & for \quad r=\infty,d\geq 3. \\
\end{cases}
\]
则对于任意 \(n \geq 1\),以至少 \(1-\exp(-n^{1-a}(\log n)^{2a})\) 的概率成立以下估计
\[\mathcal{R}(u_{n})-\mathcal{R}(u^*) \lesssim n^{-a}(\log n)^{2a}
\]
\[||u_{n}-u^*||_{H^{s}(\mathbb{S}^{d-1})} \lesssim n^{-a/2}(\log n)^{a}
\]
从结果来看,收敛速度受维度影响还是很大的. 但是在最后的实验中好像通过一个特定的网络结构避免了唯独影响. 我们先来简述证明的框架
4. 证明框架
4.1. 误差分解
定义
\[u_{\mathcal{F}} = \argmin_{u \in \mathcal{F}}R(u)
\]
\[\begin{aligned}
\mathcal{R}(u_{n})-\mathcal{R}(u^*) \leq&\left(\mathcal{R}(u_{\mathcal{F}})-\mathcal{R}(u^*)\right)+ \left( \mathcal{R}_{n}(u_{\mathcal{F}})-\mathcal{R}_{n}(u^*) -\mathcal{R}(u_{\mathcal{F}})+R(u^*)\right)\\
+&(\mathcal{R}(u_{n})-\mathcal{R}(u^*)-\mathcal{R}_{n}(u_{n})+\mathcal{R}_{n}(u^*))
\end{aligned}
\]
\(\mathcal{R}(u_{\mathcal{F}})-\mathcal{R}(u^*)\) :approximation error(逼近误差,受限于模型的表达能力)
\(\mathcal{R}(u_{n})-\mathcal{R}(u^*)-\mathcal{R}_{n}(u_{n})+\mathcal{R}_{n}(u^*)\) statisticsal error(统计误差,受限于样本数等)
$ \mathcal{R}{n}(u{\mathcal{F}})-\mathcal{R}{n}(u^*) -\mathcal{R}(u{\mathcal{F}})+R(u^*)$:Bernstein inequality
基于以下定理,我们先控制第二项
![Alt text]()
引理
\[\mathbb{E}_{p}(L(X,u)-L(X,u^*))^{2} \leq C_{0}\mathbb{E}_P(L(X,u)-L(X,u^*)) = C_0(\mathcal{R}(u)-\mathcal{R}(u^*))
\]
此处\(P\)是球面上的均匀分布,\(C_0 = (M \cdot \sum_{|\alpha|\leq s}||a_{\alpha}||_{\infty}+||f||_\infty)^{2}\),且
\[L(x,u) = |(\mathcal{L}u)(x) - f(x)|^{2}
\]
进一步的,我们有对于所有 \(t>0\),以至少 \(1-\exp(-t)\)的概率成立
\[\mathcal{R}_{n}(u_{\mathcal{F}})- \mathcal{R}_{n}(u^*) - \mathcal{R}(u_{\mathcal{F}}) + \mathcal{R}(u^*) \leq \mathcal{R}(u_{\mathcal{F}})-\mathcal{R}(u^*) + \frac{7C_{0}t}{6n}
\]
证明是计算的
证明 注意到 \(L(x,u^*) \equiv 0\)则对 \(u \in \mathcal{F}\),我们有
\[\begin{aligned}
&\mathbb{E}_{p}(L(X,u)-L(X,u^*))^{2} \\
&=\frac{1}{\omega_{d}}\int_{\mathbb{S}^{d-1}} |(\mathcal{L}u)(x) - f(x)|^{4} \mathrm{d}\sigma(x)\\
&\leq \frac{C_0}{\omega_d}\int_{\mathbb{S}^{d-1}}|(\mathcal{L}u)(x) - f(x)|^{2}\mathrm{d}\sigma(x)\\
&=C_0 \mathbb{E}_P(L(X,u)-L(X,u^*)).
\end{aligned}
\]
由上面的Bernstein inequaily, 结合基本不等式就有
\[\begin{aligned}
& \mathcal{R}_{n}(u_{\mathcal{F}})- \mathcal{R}_{n}(u^*) - \mathcal{R}(u_{\mathcal{F}}) + \mathcal{R}(u^*) \\
&\leq \sqrt{\frac{2C_0 \mathbb{E}_P(L(X,u_{\mathcal{F}})-L(X,u^*))t}{n}}+\frac{2C_0t}{3n}\\
&\leq \mathbb{E}_P(L(X,u_{\mathcal{F}})-L(X,u^*))+\frac{7C_0t}{6n}\\
&=\mathcal{R}(u_{\mathcal{F}})-\mathcal{R}(u^*) +\frac{7C_0t}{6n}
\end{aligned}
\]
接下来就是控制逼近误差和统计误差
4.2. Approximation error
先前的研究已经建立了 \(L^p\) 收敛,但是本文的目的是要建立导数同时收敛的 \(H^s\)意义下的收敛
定义了一个 near-best approximation by ploynomials \(u \in L^{p}(\mathbb{S}^{d-1})\)
\[E_{n_{0}}(u)_p = \inf_{v \in \prod_{n_{0}} }||u-v||_{p}
\]
\(\prod_{n_{0}}\) 代表次数最高为 \(n_0\)的多项式集合.
令 \(\lambda = \frac{d-2}{2}\),\(C_{k}^{\lambda}(t)\)——Gegenbauer polynomial degree-k,parameter-\(\lambda\)
定义kenerl和对应的算子
\[l_{n_{0}}(t) = \sum_{k=0}^{2n_{0}}\eta(\frac{k}{n_{0}})\frac{\lambda + k}{\lambda}C_{k}^{\lambda}(t),\quad t \in [-1,1]
\]
\[L_{n_{0}}(u)(x) = \frac{1}{\omega_{d}}\int_{\mathbb{S}^{d-1}}u(y)l_{n_{0}}(\left< x, y \right>)\mathrm{d}\sigma(x), \quad x \in \mathbb{S}^{d-1}
\]
这就是 \(L^{p}\)范数意义下的near-best approximation. 几何意义是 \(u\) 在 \(\prod_{n_{0}}\) 中的投影.
本文采用的形式(基于核)是
\[ \tilde{l}_{n_{0}}(t)= \sum^{2n_0}_{k=0}[\eta(\frac{k}{n_0})]^{2}\frac{\lambda + k}{\lambda}C^{\lambda}_{k}(t),\quad t \in [-1,1],
\]
\[\tilde{L}_{n_{0}}(u)(x) = \frac{1}{\omega_d}\int_{\mathbb{S}^{d-1}}u(y) \tilde{l}_{n_{0}}(\left< x, y \right> )\mathrm{d}\sigma(y), \quad x \in \mathbb{S}^{d-1}
\]
文中建立了如下估计:
\[||u-\sum_{i=1}^{m}\mu_i L_{n_{0}}(u)(y_i)l_{n_{0}}(\left< x, y_i \right>)||_{p} \leq C_3n_0^{-r}||u||_{W_p^r(\mathbb{S}^{d-1})}
\]
其中 cubature rule \(\{ (\mu_i,y_i) \}_{i=1}^{m}\) degree \(4n_{0}\)
\[\tilde{L}_{n_{0}}(u)(x) = \sum _{i=1}^m \mu_i L_{n_{0}}(u)(y_i)l_{n_{0}}(\left< x, y_i \right> )
\]
上面这个结果可以扩展到 \(W_p ^{s}(\mathbb{S}^{d-1}), s \le r-1\) 范数意义下的逼近
总的来说,可以做到下面的逼近
\[||u-\sum_{i=1}^{m}\mu_i L_{n_{0}}(u)(y_i)l_{n_{0}}(\left< x, y_i \right>)||_{W_p^{s}(\mathbb{S}^{d-1})} \leq C_4 n_0^{s-r}||u||_{W_p^{r}(\mathbb{S}^{d-1})}
\]
\[||L_{n_{0}}(u)(y_i)l_{n_{0}}(\left< x, y_i \right>)||_{W_p^{r}(\mathbb{S}^{d-1})} \leq C_4||u||_{W_p^{r}(\mathbb{S}^{d-1})}
\]
接下来就可以用 \(\mathcal{F}\)逼近插值:
\[||u-F^{(L+3)}||_{W_p^s(\mathbb{S}^{d-1})} \leq C_9n_0^{s-r}||u||_{W_p^r(\mathbb{S}^{d-1})}
\]
4.3. statistical error
此处考虑的应该是用HDS第四章讲的技术,利用Radamacher 复杂度控制 \(||P_n-P||_{\mathcal{F}}\),再利用VC维控制Radamacher 复杂度,此部分分析使用了局部凸分析的手段,最后得到了一个Oracle的不等式.
![Alt text]()
![Alt text]()
在主要定理的证明中,和维度有关的常数 \(a\) 是在逼近误差和统计误差的trade-off产生的
![Alt text]()
5. Sobolev \(\longrightarrow\) Korobov
这个推广其实是一个正则性减弱的过程,主要目的应该是为了克服维度给估计带来的困难.
已经有的结果是利用 \(W^{n,p}([0,1]^{d})\) DNNs 在 \(W^{m,p},m<p,1\le p\le \infty\)的逼近速率是 \(\mathcal{O}(M^{\frac{-2(m-n)}{d}})\)(乘个对数),这是一个optimal,但是还是受到维度影响.
选择 \(f(x) \in W^{2d,p}([0,1]^{d})\),在 \(L^{p}\) 范数下考虑是 \(\mathcal{O}(M^{-4})\),但是要求正则性太高(在一个方向有 \(2d\) 阶导数)
考虑一个正则性减弱的空间,可以达到一个维度无关的逼近速率,总的来说
考虑Korobov空间
![Alt text]()
可以到达下面的估计误差(optimal)
\(X^{2,p}\) convergence rate \(\mathcal{O}(N^{-4+\frac{2}{p}}L^{-4+\frac{2}{p}})\)
其中N是宽度,L是长度.



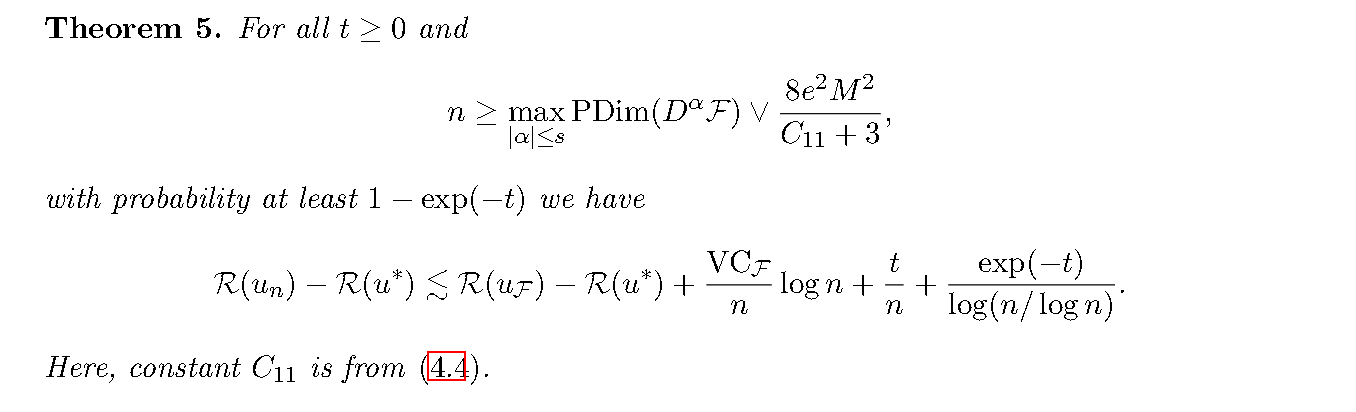
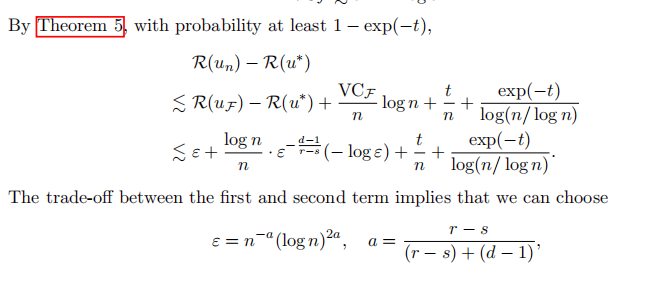
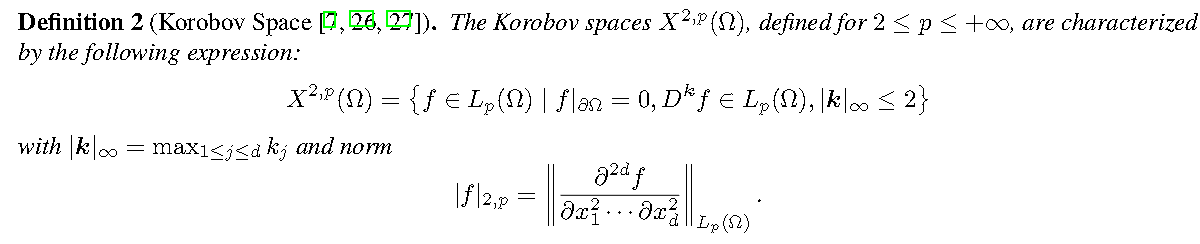




 浙公网安备 33010602011771号
浙公网安备 33010602011771号