堆

堆

1. 定义

优先队列(Priority Queue):特殊的“队列”，取出元素的顺序是 依照元素的优先权(关键字)大小，而不是元素进入队列的先后顺序

2.堆的两个特性

结构性:用数组表示的完全二叉树; 
有序性:任一结点的关键字是其子树所有结点的最大值(或最小值) 
最大堆(MaxHeap)”,也称“大顶堆”:最大值 
最小堆(MinHeap)”,也称“小顶堆” :最小值 

3.数据结构 : (完全二叉树)

因为是完全二叉树，所以可以使用数组来储存

	typedef struct HeapStruct *MaxHeap;
	struct HeapStruct { 
		ElementType *Elements; /* 存储堆元素的数组 */ 
		int Size; /* 堆的当前元素个数 */
		int Capacity; /* 堆的最大容量 
	 };

⚠️数组中的第一个元素不使用
⚠️数组中的第一个元素设为哨兵
H->Element[ 0 ] 是哨兵元素，最大(小)堆中它不小于堆 中的最大(小)元素，控制顺环结束。

4 .堆的一些基本操作集

• MaxHeap Create( int MaxSize ):创建一个空的最大堆。

• Boolean IsFull( MaxHeap H ):判断最大堆H是否已满。

• Insert( MaxHeap H, ElementType item ):将元素item插入最大堆H。

• Boolean IsEmpty( MaxHeap H ):判断最大堆H是否为空。

• ElementType DeleteMax( MaxHeap H ):返回H中最大元素(高优先级)。

  1. 堆的创建初始化

		MaxHeap Create( int MaxSize )
		{	/* 创建容量为MaxSize的空的最大堆 */
			MaxHeap H = malloc( sizeof( struct HeapStruct ) );
		    H->Elements =       malloc( (MaxSize+1)*sizeof(ElementType)); 
			H->Size = 0;
			H->Capacity = MaxSize;
			H->Elements[0] = MaxData; 
			/* 定义“哨兵”为大于堆中所有可能元素的值，便于以后更快操作 */ 
			return H; 
		} 

2. 堆的插入操作

    * 代码
   

		void Insert( MaxHeap H, ElementType item )
		{ /* 将元素item 插入最大堆H，其中H->Elements[0]已经定义为哨兵*/ 
			int I;
			if ( IsFull(H) ) { 
				printf(“最大堆已满”); 
				return;
			} 
			i = ++H->Size; /*指向插入后堆中的~最后一个元素的位置*/ 
			for ( ; H->Elements[i/2] < item; i/=2 ) 					    /*哨兵元素在这里起作用了哦，因为堆中所有元素都小于哨兵元素，所以限制了最大元素继续上移*/
				H->Elements[I] = H->Elements[I/2]; /* 向下过滤结点 */ 
		H->Elements[I] = item; /* 将item 插入 */ 
		} 

	* 图解

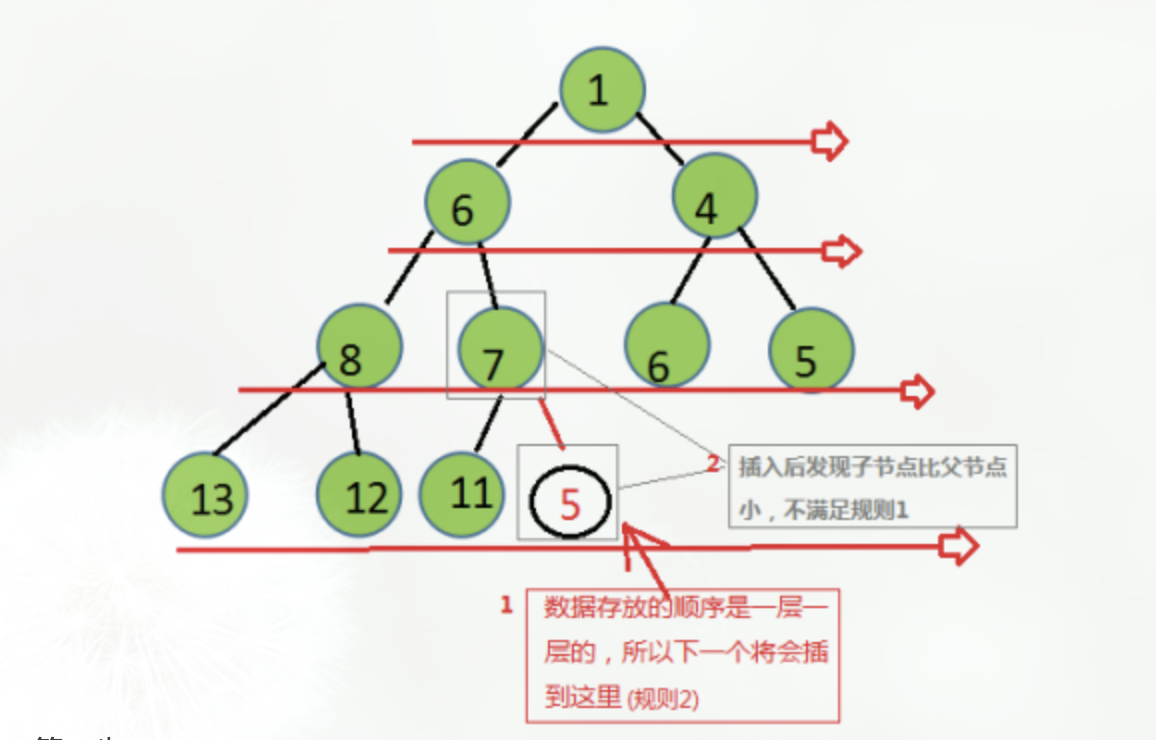
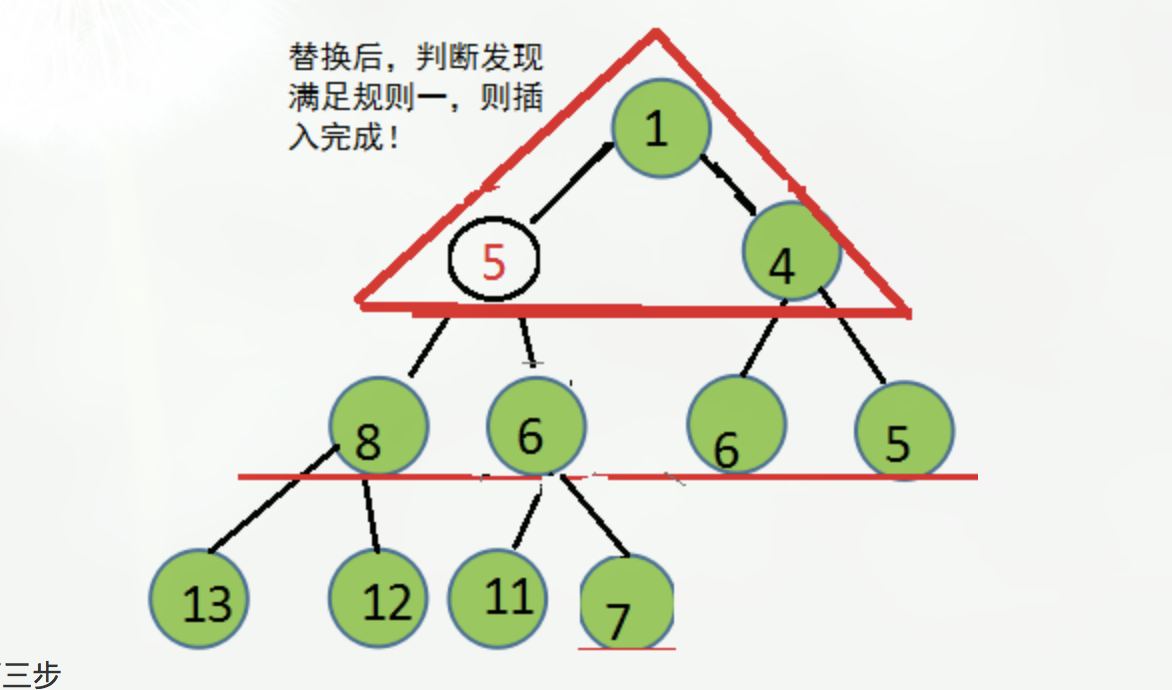
3. #### 堆的删除操作

		ElementType DeleteMax( MaxHeap H ) 
		{ /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */ 
			int Parent, Child;
			ElementType MaxItem, temp;
			if ( IsEmpty(H) ) { 
				printf(“最大堆已为空”); 
				return; 
			} 
			MaxItem = H->Elements[1]; /* 取出根结点最大值 */
			/* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */ 
			temp = H->Elements[H->Size—];
			for( Parent=1; Parent*2<=H->Size; Parent=Child ) { 
        			Child = Parent * 2; //此时chlid指向右节点
        			if( (Child!= H->Size) &&(H->Elements[Child] < H->Elements[Child+1]) ) /* Child指向左右子结点的较大者 */ 
					Child++; 
				if( temp >= H->Elements[Child] ) /*temp大于Child指向左右子结点的较大者*/
					break; /*此时break出来表示此时的parent就是temp元素要放置的位置*/
				else /* 移动temp元素到下一层 */ 
					H->Elements[Parent] = H->Elements[Child]; 
			}
			H->Elements[Parent] = temp; 
			return MaxItem; 
		}

	⚠️理解:first弹出根结点元素，second将二叉树叶子结点的最右边的节点(即)放置到根结点的位置（不是真放），third将根结点与左右子节点中的最大节点比较，小于则将子节点上移。

4. 最大堆的建立

   void create(MaxHeap H,int N){
	   	ElementType a;
	   	for(int I=0;i<N;i++){
			scanf(“%d”,&a);
			insert( H,a );
		}