2022年7月17日总结

cf比赛:　三场

　　div4的简单场,但是差一个题目ak,后面的题目写的有点慢了,所以最后一题时间不够了

 

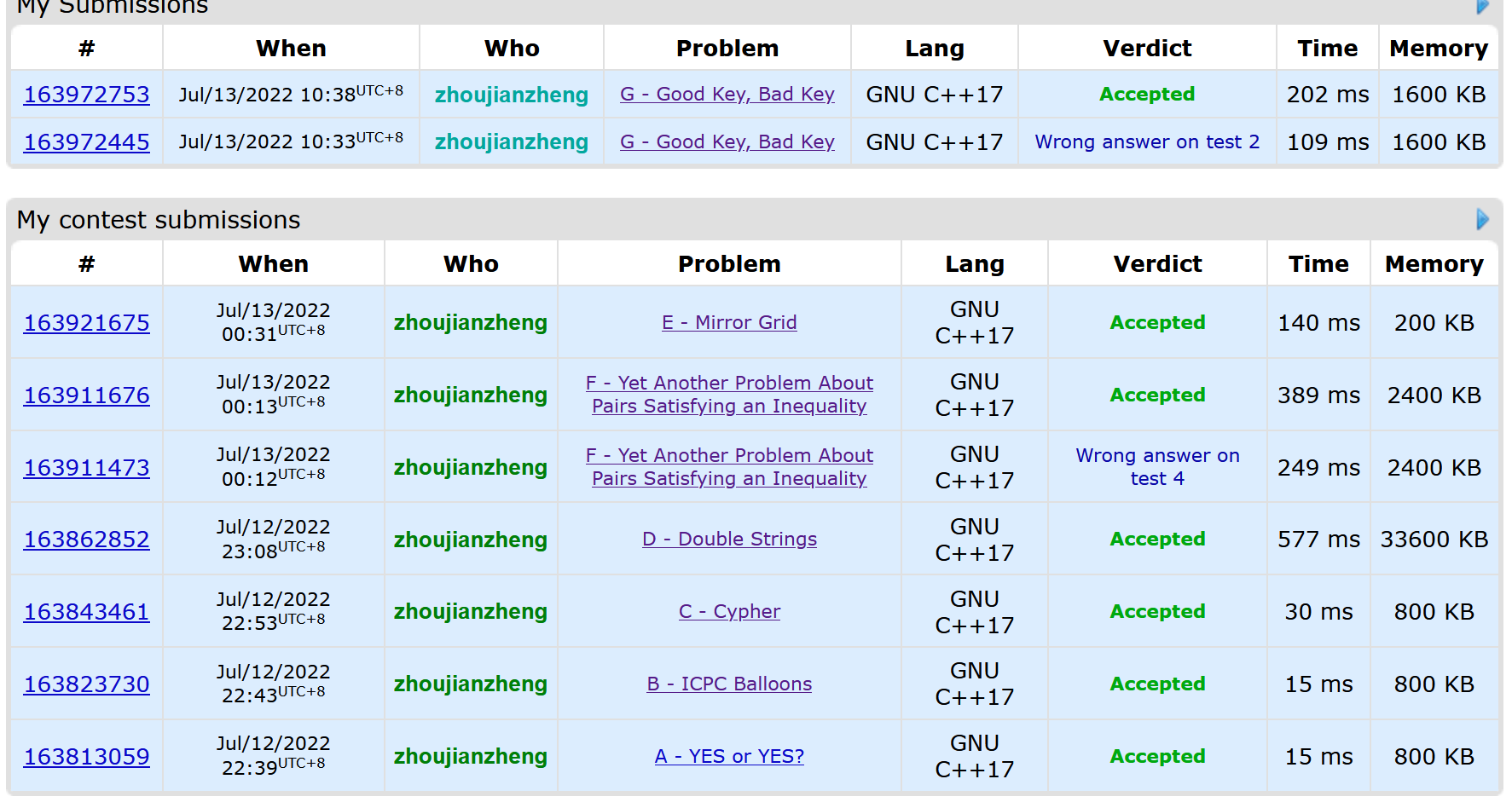
 　　第二场:

 

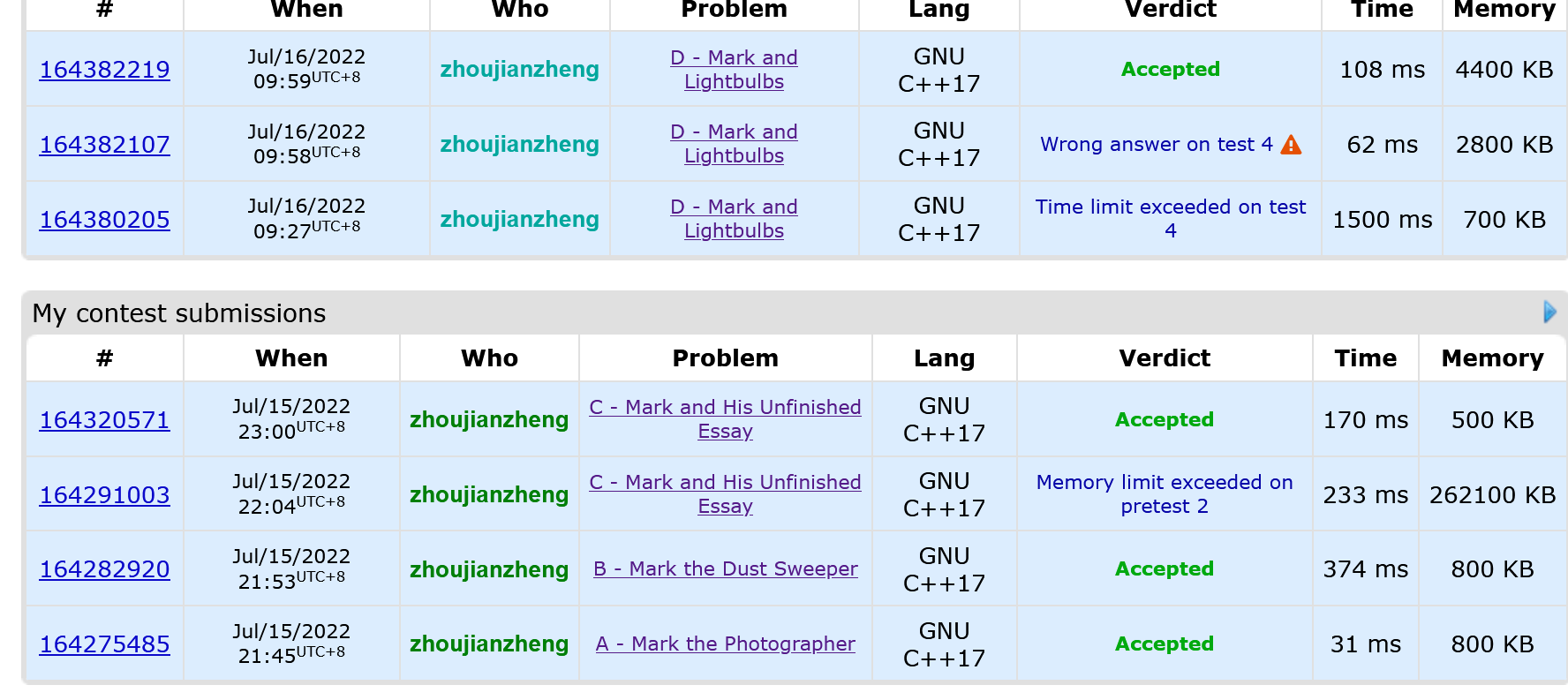
 第三题想慢了,第四题没有想到点上

　　第三场:

　　

 

 目前为止状态最好的一场,三个题差不多三十分钟,首次进入前一千

 

 

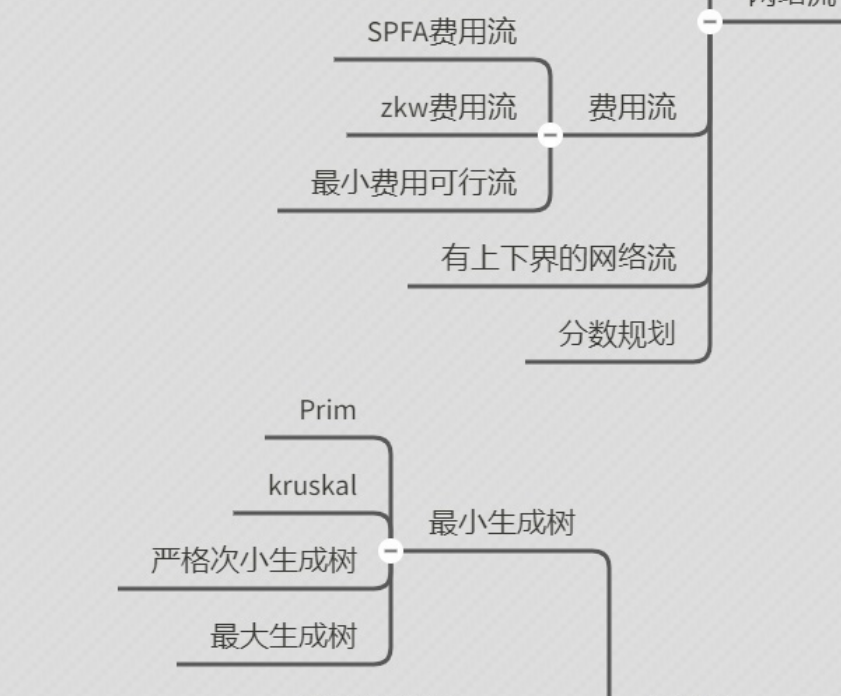
　树的直径:

　　　　作用:计算一棵树的中最长的最短路.

　　　　计算方法:

　　　　　　1.两次bfs:随机选择一个节点通过bfs求出距离该节点最远的节点a,再次bfs求出距离节点a最远的节点b,那么ab就是这颗树的直径,该算法可以计算出直径的路径

　　　　　　2.树形dp:通过一次bfs的回溯累计权值,每个节点计算最大的两个子节点的累计权值的最大值就是最终的直径长度,该算法无法计算出直径的路径,只能够获取直径的长度

　　二分图:

　　　　二分图的最大匹配

　　　　　　作用:计算最优的两两匹配方案

　　　　　　算法:

　　　　　　　　匈牙利算法:递归配对,如果当前1要求配对1',如果1'没有配对那么1和1'配对成功,否则如果1'已经和2配对,那么询问2是否能够与1'以外的人配对以此循环,如果全部成功配对,那么配对数+1;

　　　　二分图最大权完美匹配
　　　　　　作用:计算出带权两两匹配的最大累计权值

　　　　　　算法:　

　　　　　　　　KM算法:基于匈牙利算法的改变,对每个匹配方给一个期望为最大的匹配权值.被匹配方的期望为0,每次匹配都匹配为匹配方和被匹配方的权值等于配对方的期望加上被配对方的期望,如果两者相等,那么两者匹配,否则不匹配,基于此附加规则下的匈牙利算法,如果交替路成立才遍历下一个节点,否则将交替路上的所以匹配方的期望-=最小差值min(匹配方的期望+被匹配方的期望-匹配方与被匹配方的权值).被匹配方则+=最小差值

 

　　网络流:

　　　　网络最大流:

　　　　　　作用:计算网络的最大流问题

　　　　　　算法:

　　　　　　　　ek算法:bfs用来遍历s(起点)到t(终点)的路径同时沿途累加网络流,如果bfs能够遍历出s-t的路径,那么将路径上对应的所有边的前驱+=mi(路径上的最小权值),后驱-=mi,直到bfs无法遍历出s-t的路径,那么最终t节点累加的值就是网络的最大流.

　　　　　　　　dinic算法:ek的进阶版本,ek算法每次只会扩展一条增广路,dinic算法通过bfs检测起点和终点的连通性,再通过dfs算法去遍历bfs路径中的增广路同时更新残留网络,和ek算法不同的是dinic算法每次可以更新一条以及以上的增广路,算法复杂度为n*n*m,而ek算法n*m*m,边的数量一般大于点的数量,算法复杂度而言,dinic算法优于ek算法

 

 总结:这个星期打比赛的状态都挺不错,学习进度比较的平稳,本周网络流和二分图基本学了个七七八八,做题过程中写了也遇到了一些其他的一些不是特别出名,但是有点用的算法,比如说数的直径的计算,也算是增长了见识

下周比赛等一些事物可能就多一些了,暂定目标为下面这些.