总结

比赛:

　　三场cf:　

　　　　第一场

 

 

c题拜在了数学组合上面了.a,b做的慢了些,总体来说也没打好

　　　　第二场

这次a,b速度还行,就是a题wa了一次,有点小可惜,c题可以说是最可惜的,一看题就知道是一个二分答案的题目,但是有个细节没有注意,就是工人少了一个小时的处理,我是让他补了一个小时,正解是让他空着不用管,写了一个多小时的二分没有写出来,应该算是最可惜的了吧

 　　　　第三场

 

 

这一场没有打,那一天确实是忘记打了,早上还记得,晚上就忘记了.后面自己测了一下,a,b,c,d差不多半个多小时,中间上了个厕所.而且e题也是半个小时内也写出来了,f题确实有点无从下手,后序看题解,看了一个小时,也是只看懂了过程,没有完全理解其中的原理

　　一场算法组测试赛

 

 

 很遗憾拿了个倒数,a题和b题都是dp题,a类似于背包问题,感觉就算是比赛的时候我应该也写不出,b题是一个线性dp,而且带有优化.

第五题,挺简单的一个题,统计计数O1的复杂度,代码也不复杂,比赛的时候没有看这个题,就算看到感觉也要想一会儿

第六题:最不应该错的题目,简单来说就是查找一个数在那个范围里面,题目给出的负号给了我一定的干扰,当时一直在纠结题目给出的负号到底是2个字节的还是1个字节的,因为复制过来的时候是两个字节的,然后我也很单纯的把那个很大的数转换成了数字.忘了本身string就是可以直接进行比较的了.比完后,我自己重新再写了一次.一遍就过

总结一下这次的测试:错误率太高,题目没看清,其中有2个题都是题目没有完全看明白直接就下手了,然后白白罚时.有点小心急.,还有就是写的时间着实有点久了,从第一个题到最后一个题差不多就一个多小时一点,但是第一个题是一个半小时的时候才交的.

 

最近学习的内容:

　　　spfa算法:

　　　　作用:寻找单源最短路,判负环,

　　　　算法原理:和迪杰斯特拉算法原理类似,效率比迪杰斯特拉算法低一些,但是可以判断负环

　　　　　　　　从起点开始像外扩展边dist[i]=min(dist[i],dist[j]+v);如果一个节点的dist值被更新了n次那么一定有负环

　　　　两种优化:两种优化只有在权值为随机值的时候才有更好的效果,否则可能会被恶意卡点达到指数级的复杂度,类似于迪杰斯特拉的优先队列优化

　　　　　　　　SFL优化:

　　　　　　　　　　优化原理:将更新后节点小于队列前端的节点放到队列前面,否则放到队列后面

　　　　　　　　LL优化:

　　　　　　　　　　优化原理:从队列中选择节点的时候,如果当前节点的dist大于平均值,将该节点放到最后面,直到取的当前节点的dist小于平均值的时候才进行节点更新

　　　　bellman_Ford算法:

　　　　　　作用:单源最短路,判断负环

　　　　　　算法原理:暴力更新最短边,如果第n次的时候还能够更新,那么一定有负环.

　　　　A*算法:当目标点不可到达的时候,A*算法不如暴力bfs

　　　　　　作用:让bfs更加的智能(加了优先队列的bfs)

　　　　　　算法原理:通过曼哈顿距离(其他的计算函数)估算出当前节点到目标节点的价值,优先选择价值小的点扩展.

　　　　最长路:将所有的权值变成负数,跑最短路,最终结果的负数就是最长路

　　　　tarjan算法:

　　　　　　强联通分量:

　　　　　　　　概念:访问强联通分量中的任何一个点就可以访问强联通分量中的所有点,可以将强联通分量中的所有的点看做是一个点(缩点)

　　　　　　　　判断:如果当前节点的时间戳没有被更新,那么当前节点以及被遍历到的所有节点属于一个强联通分量

　　　　　　割边(桥):

　　　　　　　　概念:如果删除一条边,会影响图的连通性,那么这条边就是割边(桥)

　　　　　　　　判断:tarjan遍历的时候,如果子节点的时间戳没有被更新,那么子节点和父节点之间的连接就算一条桥(nfs[pre]<low[gol])   　　如果是无向图那么当一个节点既是另一个节点的儿子又是另一个节点的父亲的时候不作任何判断.

　　　　　　割点:

　　　　　　　　概念:如果删除一个点,会影响图的连通,那么这个点就是割点

　　　　　　　　判断:如果当前节点为根节点并且儿子的个数>=2的时候,当前节点为割点..如果当前节点不是根节点并且当前时间戳小于等于子节点的最小时间戳

 

 

 

 

 

总结:

　　　学习的新知识不是很多,更多的是对原来学习内容的巩固以及扩展.

　　后序规划:

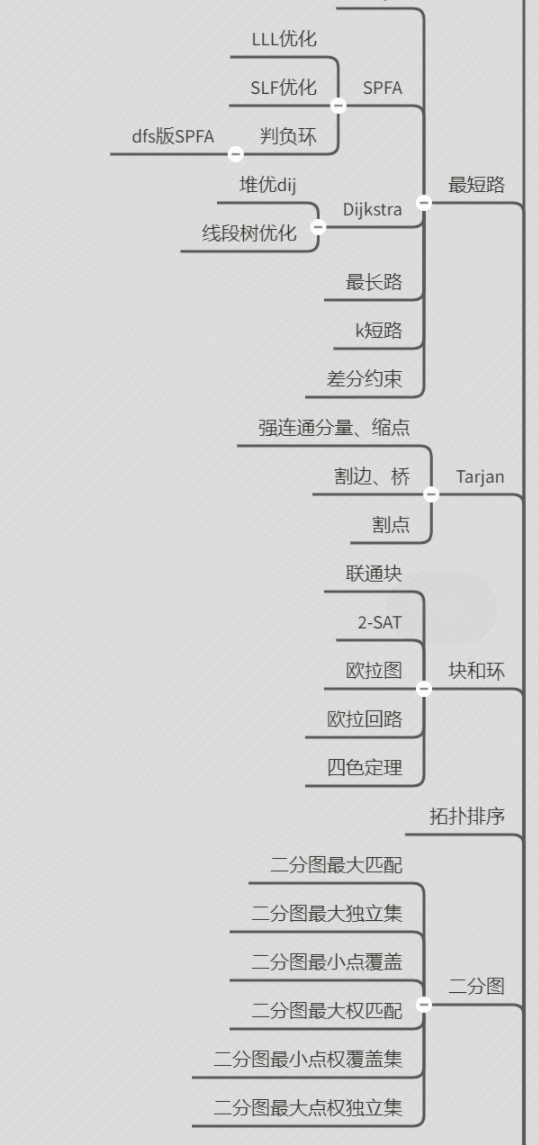
　　　　根据算法树一步一步来