比赛链接
link to the contest
知识点 & 总结
- K:离散情况讨论大小关系,要考虑是 \(x \le y, x \le y-1, x < y-1\) 中的哪一种
题解
B - Shuttle Bus
- 先考虑固定 \(t = r\) 的时候怎么做:
- 记:以 \(r\) 为根时, \(u\) 为根的子树大小为 \(s_u\)
- 假设方案中被至少一条路径覆盖了的点集(不包含 \(r\))为 \(S\),此时的总步行距离为 \(\sum_{u \neq r} dis(u, r) - \sum_{u \in S} s_u\),而前者是个与路径选取方案无关的定值,于是问题转化为最大化被路径覆盖的点的 \(\sum_{u \in S} s_u\),记这个和为 \(X\)
- 转化后的问题可以贪心解决,即每次加入 \(X\) 增量最大的路径,总共操作 \(k\) 次
- 考虑用数据结构维护所有路径的“增量”:观察到,当 \(t\) 变为它的一个邻居时,这些增量构成的集合只有 \(O(1)\) 个(实际上是两个)元素会发生变化;我们所需要求的是前 \(k\) 大增量的和
- 使用平衡树或者两个 STL multiset 就可以完成这些操作,复杂度为 \(O(n \log n)\)
- 代码:B
C - Selection Sort Count
- 假设伪代码中 \(i = k\) 时,在 \(j = j_1, j_2, j_3, \cdots j_{l_k}\) 进行了交换,此时序列中的 \(P_i, P_{j_1}, P_{j_2}, \cdots P_{j_{l_k}}\) 将会依次变成 \(P_{j_{l_k}}, P_i, P_{j_1}, P_{j_2}, \cdots P_{j_{l_k - 1}}\),交换次数 \(t_k = l_k\)
- 观察发现:
- \(i = k\) 时的 \(\{j_1 \cdots j_{l_k}\}\) 序列与 \(i = k+1\) 时相比,前者去掉 \(j_{l_k}\) 以后必然是后者的子序列
- (猜测)反之,如果有一组满足上面条件的 \(j\) 序列,则可以唯一还原出排列 \(P\)
- 于是答案为 \(\prod_i \binom{(t_i - t_{i-1} + 1) + (t_{i-1} + 1) - 1}{(t_{i-1} + 1) - 1} = \prod_i \binom{t_i + 1}{t_{i-1}}\)(往 \(t_{i-1} + 1\) 个可以为空的盒子里放入 \((t_i - t_{i-1} + 1)\) 个球)
- 代码:C
I - Reverse LIS
- 不考虑翻转操作:
- 假设某个上升子序列从原数组下标 \(k\) 处“隔断”,即 \(k\) 之前子序列取
0、\(k\) 之后子序列取 1,则这样上升子序列的最大长度=(k之前的0个数)+(k之后的1个数)=(1总数)+(k之前的0个数)-(k之前的1个数)
- 于是问题转化为求一个
(k之前的0个数)-(k之前的1个数)最大的前缀
- 将
0的位置赋为 \(1\),将 1 的位置赋为 \(-1\),问题就转化为求最大前缀和
- 注意到 \(k\) 一定不会取在连续相同字符的中间,所以可以把连续相同的一段的
0/1 合并在一起,即 a[i] = (c[i] == '0' ? 1 : -1) * p[i],求 a[i] 的最大前缀和
- 允许至多 \(m\) 次翻转,等价于取一段前缀、以及至多 \(m\) 段不相交的区间,最大化所取元素的和
- 对下面建图模拟费用流:每次选出最大的区间(第一次取前缀),并且将选过元素全部修改为相反数,重复操作至多 \(m\) 次
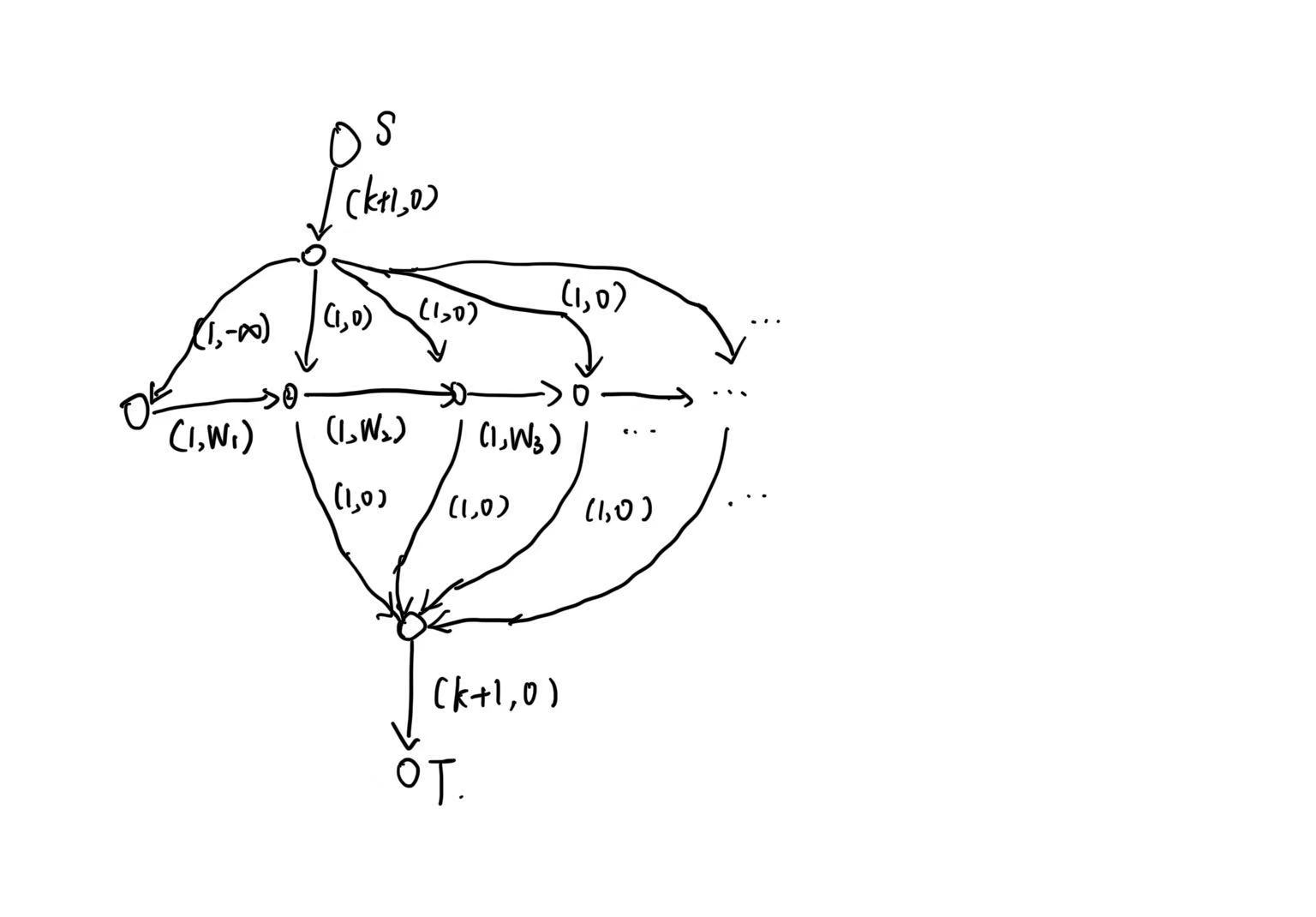
- 用线段树维护即可
- 代码:
K - Security Plan
- 代码:K
- 讨论如下(图中是 \(3\times 5\) 的样例):
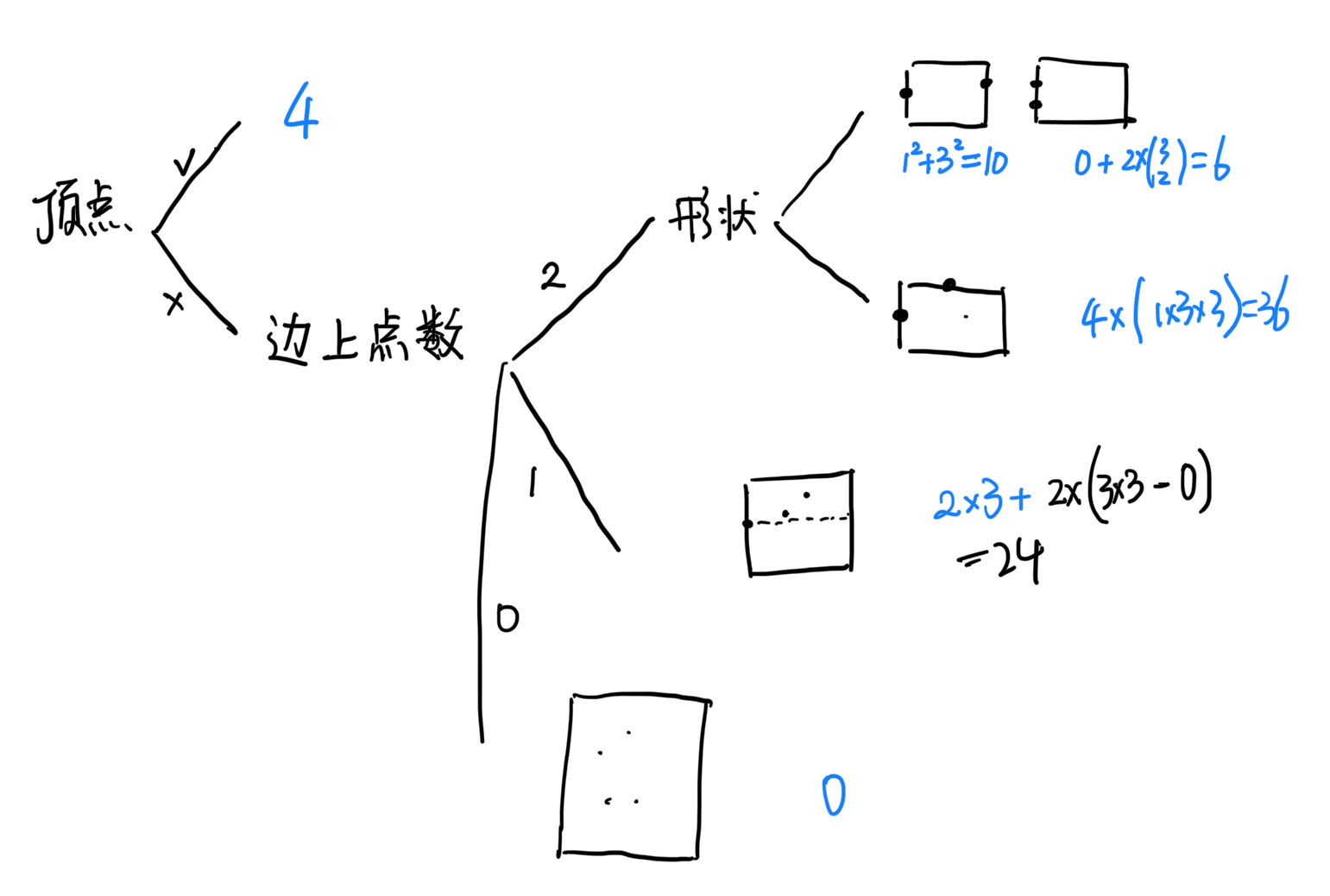
posted @
2025-05-19 19:19
zhongyuwei
阅读(
74)
评论()
收藏
举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号