CCPC Final 2020 第六届中国大学生程序设计竞赛总决赛 补题 (20240423训练)
目录
比赛链接
知识点 & 总结
- B
- “枚举因子”的思路
- F
- 在环上,\(n\) 个区间的交不一定是 \(O(1)\) 个区间的并
- G
- 归纳思想
- J
- 考虑区间dp
- L
- 注意叉乘是不能用来给斜率排序的
题解
B - Algebra
- \(x^n + ax + b = 0 \Leftrightarrow x (x^{n-1} + a) = b\)
- 枚举 \(b\) 再枚举 \(b\) 的因子 \(x\),总复杂度是 \(O(m\ln m)\) 级别的,可以接受。
- 代码:B
E - Game Theory
-
根据 IMO2019 shortlisted problems 中 C3 的 Solution 3,设 \(H_i\) 表示前 \(i\) 个字符中
1的个数,\(t(i)\) 表示第 \(i\) 个字符被反转的次数,则:\(t(i) = [s_i = 1] + 2 ( \min\{i - H_i, H_n - H_i\})\) -
可以从这个示意图看出来:\(i - H_i\) 对应 \(i\) 左边的
0的数量,\(H_n - H_i\) 对应 \(i\) 右边的1的数量
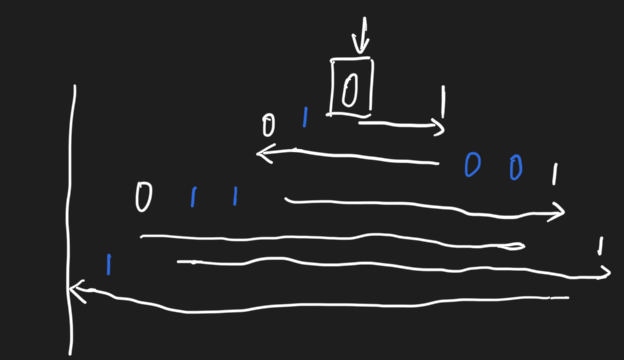
-
于是答案就是 \(\sum_{i=1}^n t(i) = H_n + 2(\sum_{j=1}^{H_n}i + \sum_{j=H_n+1}^n H_n) - 2\sum_{j=1}^n H_i = 2(n+1)H_n + H_n^2 - 2\sum_{i=1}^n H_i\)
-
线段树维护区间的 \(H_r\) 和 \(\sum_{i=l}^r H_i\) 即可
-
代码:E
G - Hamilton
- 只需让 \(c_1 \cdots c_{n-1}\) 满足题目条件(此时的 \((p_1, p_2, \cdots p_n)\) 和 \((p_n, p_{n-1} , \cdots p_1)\) 中至少有一个可以使得 \(c_1 \cdots c_{n-1}c_n\) 满足题目条件)
- 归纳地构造解:
- 假设处理完元素 \(1, 2, \cdots m\),获得了一个长度为 \(m\) 的排列,其中第 \(1\) 个到第 \(q\) 个点之间是 0 边,第 \(q\) 个到第 \(m\) 个点之间是 1 边
- 考虑 \(C_{m + 1, q}\) 的颜色:
- 若为 0,则将 \(m+1\) 放在 \(q\) 的后面,此时无论 \(m+1\) 的另一条邻边是什么颜色,整个序列仍然合法
- 同理,若为 1,则将 \(m+1\) 放在 \(q\) 的前面,整个序列仍然合法
- 代码:G
J - Permutation Pattern
- 区间 dp,
f[l][r][lb][rb]表示考虑了下标在[l,r]中的元素,选出的元素(不可以不选)最大、最小值分别为lb,rb,对应的方案数 - 假设某个方案中,选出元素的最大值下标为
m,则我们要求这个方案只能够通过f[l][m-1] * f[m+1][r]进行计算。这样既能保证某个方案对f的贡献路径唯一,也能检查是否出现不合法的 pattern。 - 代码:J
L - 2D Geometry
- 假设共线的点最多有 \(k\) 个:
- 若 \(k > 2(n - k)\),则答案显然为 \(k - 2(n - k)\)
- 否则,(猜测)答案为 \(n \bmod 3\)
- 注意到 \(k > 2(n-k) \Leftrightarrow k > \frac{2}{3} n\),故而随机 \(O(\log n)\) 条线、判断线上的点数是否超过 \(\frac{2}{3}n\) 即可
- 代码:L
M - 3D Geometry
- 通过翻转和平移变换,使得棱锥在 \(x \ge 0, y \ge 0, z \ge 0\) 的区域内且四个顶点形如 \((0, 0,0), (x, 0, 0), (0, y, 0), (0,0, z)\)
- 通过差分,将立方体区域转化为形如 \(\{ (x, y, z): x \ge a, y \ge b, z \ge c\}\) 的区域。这样的区域与棱锥的交为空集或者与原来棱锥相似的棱锥,相似棱锥的体积可以通过点 \((a, b, c)\) 与原点到棱锥斜面的距离之比导出。
- 代码:M


 浙公网安备 33010602011771号
浙公网安备 33010602011771号