P10834 刷题记录

前言

别和作者一样有唐诗问题
作者的代码实现能力一向很好，所以直接一遍写出来了，但是调了三天
首先检查你的 pushup 中是否清零了

题意

首先有 \(n\) 个正方形，每一个正方形有一个边长，全都是黑色的，一次操作将会合并两个正方形，合并方式为对其他们的中心，如果他们某一个位置都是黑色或者白色，合成出来的正方形就会使白色，否则是黑色，一次的贡献为两个正方形的黑色部位重叠位置面积，可能会将合并过了的正方形在合并一遍，每一次都要统计贡献。理解不了的可以看图：

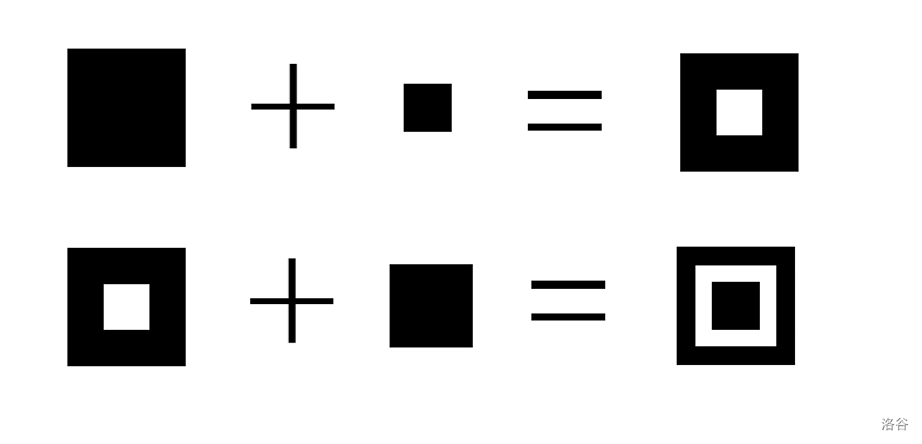
做法

首先考虑到整个正方形会是很多个环，但是这样太复杂了，不如只考虑右下角，其它部分的贡献和右下角一样，所以乘四即可。
然后就变成左上角对齐的正方形了，然后抽象一个正方形为 \(a_i\times a_i\) 为黑色剩下为白色的正方形，那么这样就可以干掉大小限制，然后发现区间变为黑色太复杂了，不如使用差分标记，如果左边存在奇数个标记就是黑色，否则就是白色。
然后发现如果合并两个正方形的时间复杂度一定会超过 \(\log_2n\)，那么不如尝试均摊 \(\log_2n\) 的做法，可以使用线段树合并维护整个过程，具体的对于每一个区间记录 \(tag,num\)，分别表示一个区间的标记个数和左边为奇数个标记的点的贡献和，合并的时候记录左边有多少个标记，然后每一次无法递归时记录答案即可。

代码

#include<algorithm>
#include<iostream>
#include<cstring>
#include<climits>
#include<cmath>
#define ll long long
#define endl '\n'

using namespace std;
const int N=1e5,Lg=16,M=1e6+9;
ll ans;

struct SGT{
    int lson[N*Lg*4],rson[N*Lg*4];
    ll tag[N*Lg*4],num[N*Lg*4];
    int now,stk[N*Lg*4],cnt;

    inline int newnode(){
        int node=(now?stk[now--]:++cnt);
        lson[node]=rson[node]=tag[node]=num[node]=0;
        return node;
    }

    inline ll calc(ll l,ll r){
        return r*r-(l-1)*(l-1);
    }

    inline void pushup(int id,int l,int r){
        int tagl=0;
        tag[id]=tag[lson[id]]+tag[rson[id]];
        num[id]=0;
        if(lson[id]){
            tagl=(tag[lson[id]]&1);
            num[id]+=num[lson[id]];
        }
        int llt=(l+r>>1)+1,lrt=r;
        // cout<<id<<' '<<tagl<<' '<<l<<' '<<r<<' '<<lson[id]<<' '<<num[lson[id]]<<' '<<rson[id]<<' '<<num[rson[id]]<<endl;
        if(tagl){
            num[id]+=(calc(llt,lrt)-num[rson[id]]);
        }else{  
            num[id]+=num[rson[id]];
        }
        return void();
    }

    inline void change(int id,int l,int r,int x){
        if(l==r){
            tag[id]++;
            if(tag[id]&1)
                num[id]=calc(l,l);
            else num[id]=0;
            return void();
        }
        int mid=l+r>>1;
        if(x<=mid){
            if(!lson[id]) lson[id]=newnode();
            change(lson[id],l,mid,x);
        }else{
            if(!rson[id]) rson[id]=newnode();
            change(rson[id],mid+1,r,x);
        }
        pushup(id,l,r);
    }
    inline int merge(int x,int y,int l,int r,int ltagx,int ltagy){
        // cout<<x<<' '<<y<<' '<<l<<' '<<r<<' '<<ltagx<<' '<<ltagy<<' '<<ans<<endl;
        // cout<<tag[x]<<' '<<num[x]<<' '<<tag[y]<<' '<<num[y]<<endl;
        if(!x || !y){
            if(!x && !y){
                if((ltagx&1) && (ltagy&1))
                    ans+=calc(l,r);
                return 0;
            }

            if(!x){
                // cout<<y<<' '<<l<<' '<<r<<' '<<num[y]<<endl;
                if((ltagx&1) && !(ltagy&1))
                    ans+=num[y];
                else if((ltagx&1) && (ltagy&1))
                    ans+=calc(l,r)-num[y];
                return y;
            }else{
                if((ltagy&1) && !(ltagx&1))
                    ans+=num[x];
                else if((ltagy&1) && (ltagx&1))
                    ans+=calc(l,r)-num[x];
                return x;
            }
        }
        if(l==r){
            if(((ltagx+tag[x])&1) && ((ltagy+tag[y])&1)) ans+=calc(l,l);

            tag[x]+=tag[y];
            stk[++now]=y;
            if(tag[x]&1) num[x]=calc(l,l);
            else num[x]=0;
            return x;
        }
        int mid=l+r>>1;
        rson[x]=merge(rson[x],rson[y],mid+1,r,ltagx+tag[lson[x]],ltagy+tag[lson[y]]);
        lson[x]=merge(lson[x],lson[y],l,mid,ltagx,ltagy);
        stk[++now]=y;  
        pushup(x,l,r);
        // cout<<"point "<<x<<' '<<l<<' '<<r<<' '<<tag[x]<<' '<<num[x]<<' '<<lson[x]<<' '<<rson[x]<<endl;
        return x;
    }
}seg;

int root[N<<1],n,a[N<<1];

inline int rt(int x){
    return (root[x]?root[x]:root[x]=seg.newnode());
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        seg.change(rt(i),1,M,1);
        seg.change(rt(i),1,M,a[i]/2+1);
    }

    for(int i=1;i<n;i++){
        ans=0;
        int x,y;
        cin>>x>>y;
        root[i+n]=seg.merge(rt(x),rt(y),1,M,0,0);
        cout<<ans*4<<endl;
    }
    return 0;
}

bug

容易出现的问题：

• 1.不清0

学到的 trick：

• 1.将问题转化