P11203 解题报告

前言

看见树状数组就闻着味过来了
但是怎么都写题解去了，题解区全是同学的，这边赶工出来一份
个人认为很好的题目，建议深度思考
他可以带来很多启发，不一定就是简单的一些算法的叠加

本文需要知道的算法有：倍增、树状数组、离散化
其实最主要的还是倍增，可以点出整体的算法的核心

传送门

有 luogu题解部分，不确定有更好的阅读体验

题目意思

题目其实很简洁了可以直接看，这里解释一下
如果一个人会被另一个人感染，当且仅当他们同时存在的时间区间 \([l,r]\) 长度超过了给定时间 \(x\)，现在有 \(n\) 个人，知道他们的存在时间 \([l_i,r_i]\)，\(q\) 次询问，每次给定传染源 \(p\) 和感染常数 \(x\)，求每一次感染会感染多少个人，未要求强制在线

思考过程

这里提供思考过程，希望直接知道怎么做的可以直接看下面的做法部分

首先题目给出了 \(q\) 组询问，很多时候我们可以将多次询问转化成离线问题，比如二维数点类似的扫描线算法，并且就算将问题离线下来之后，我们也可以逐一求解，类比在线，所以对于多组询问问题，离线是显然不错的

第二步，观察题目性质，发现很难入手，没有什么切入点，那么考虑暴力，暴力做法是将所有现在能被感染的人设为感染状态，然后不停的扩散直到无法感染为止，所以时间复杂度是 \(\mathcal{O}(n^3q)\) 能过 21pts，部分分不高但是是一个很好的切入点

考虑将感染过程优化，将一个询问中一个人向他能感染的人连边，如下图（读者可以自行从一堆样例里面随便选一个手玩）

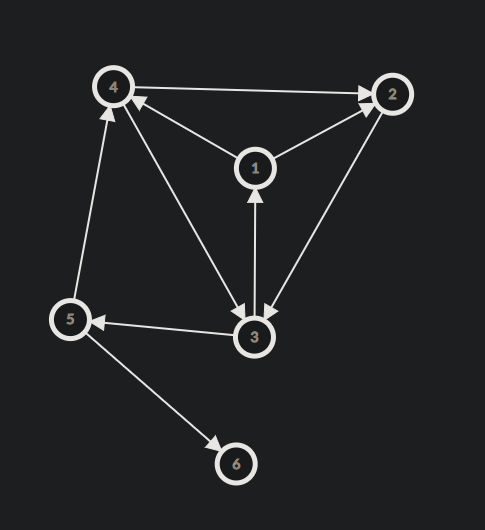
不仅如此，手玩多次之后会发现一个很有趣的现象，我们的感染路径从开始位置一直走可以找到一条链，使得这个链经过所有节点，比如上图，可以找到 \(1\to 4\to 2\to 3\to 5\to 6\)，发现这个规律之后我们就不需要再这个图上面找大小了，可以直接找链长，思考这个为什么是对的，找到这个链，发现这个链的每一个节点传染到的下一个节点是 \(r_j\ge r_i\) 且 \(l_j\) 最小的点，很关键的一点是，这两个点之间满足如果他们两之间不可以传染，别的点也不可能跟他传染，原因为这两个点之间既满足了一定有交且交最大。

所以可以预处理每一个节点下一次传染的人是谁，接着他的传染路径可以使用倍增优化，关于 \(x\) 的问题，就直接记录一个辅助数组表示从 \(i\) 开始传染 \(2^j\) 步的 \(x\) 至少要是多少，这样就可以倍增一直找到传染的链长了

所以就做完了……吗

会发现一个问题，如果我们现在有一个点在餐厅的时间非常短，可能只有一分钟，那么这个人铁定不会被感染，但是我们的倍增可能会把他算进来，而且如果一个人在感染源进来之前就进来了，也会算不到这个人的贡献

考虑怎么处理这个问题，我们这个链的开头和结尾有什么性质，发现这个链的所有节点涵盖了所有感染者的时间，所以我们相当于找到了感染时间的左端点和右端点

接下来的就好做了，我们只需要找到所有右端点在感染源右端的所有点，并且找到和感染区间交集超过 \(x\) 的所有节点即可

做法

按照 \(r_i\) 排序，预处理出每一个节点下一个传染的人是谁，查询时在线倍增出感染区间左右端点，然后离线下来，下一步是按照每一个节点的区间长度加入这个点，对于每一个询问树状数组求交集即可。

代码

//上面如果讲的不够清楚可以看这里
#include<algorithm>
#include<iostream>
#include<cstring>
#include<climits>
#include<cmath>
#define ll long long

using namespace std;
const ll N=2e5+9;
struct person{ll l,r,id;}a[N],c[N];
struct query{ll l,r,mn,id;}que[N];
ll nxt[N][25],lg[N],g[N][20];
ll n,q,book[N],ans[N];

inline bool cmp(person x,person y){
    return x.r<y.r;
}
inline bool cmpp(person x,person y){
    return (x.r-x.l)>(y.r-y.l);
}
inline bool Cmp(query x,query y){
    return x.mn>y.mn;
}

struct seg{
    #define lowbit(x) (x&(-x))

    int tr[N];
    inline void change(int x,int y){
        for(;x<=n;x+=lowbit(x))
            tr[x]+=y;
    }
    
    inline int query(int x){
        int sum=0;
        for(;x;x-=lowbit(x)){
            sum+=tr[x];
        }
        return sum;
    }
}seg;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i].l>>a[i].r,a[i].id=i;
    sort(a+1,a+n+1,cmp);
    ll mn=INT_MAX,pos=0;
    for(int i=2;i<=n;i++)lg[i]=lg[i>>1]+1;
    for(int i=n;i>=1;i--){
        nxt[i][0]=0;
        g[i][0]=INT_MIN;
        if(i!=n){
            nxt[i][0]=pos;
            g[i][0]=a[i].r-max(a[i].l,a[pos].l);
        }
        if(a[i].l<mn){
            mn=a[i].l;
            pos=i;
        }
    }
    for(int i=1;i<=lg[n];i++)
        for(int j=1;j<=n;j++){
            nxt[j][i]=nxt[nxt[j][i-1]][i-1];
            g[j][i]=min(g[j][i-1],g[nxt[j][i-1]][i-1]);
        }
    for(int i=1;i<=n;i++)book[a[i].id]=i;
    cin>>q;
    for(int i=1;i<=q;i++){
        int p,x;
        cin>>p>>x;
        que[i].l=a[book[p]].l;
        p=book[p];
        for(int j=lg[n];j>=0;j--)
            if(x<=g[p][j])
                p=nxt[p][j];
        que[i].r=a[p].r;
        que[i].mn=x;
        que[i].id=i;
    }
    for(int i=1;i<=n;i++)
        c[i]=a[i],c[i].id=i;
    sort(c+1,c+n+1,cmpp);
    sort(que+1,que+q+1,Cmp);
    ll now=1;
    for(int i=1;i<=q;i++){
        while((c[now].r-c[now].l)>=que[i].mn && now<=n)
            seg.change(c[now].id,1),now+=1;
        int lt=1,rt=n,ans1=-1;
        while(lt<=rt){
            int mid=lt+rt>>1;
            if(a[mid].r>=que[i].l+que[i].mn) ans1=mid,rt=mid-1;
            else lt=mid+1;
        }        
        int ans2=-1;
        lt=1;rt=n;
        while(lt<=rt){
            int mid=lt+rt>>1;
            if(a[mid].r<=que[i].r) ans2=mid,lt=mid+1;
            else rt=mid-1;
        }
        if(ans1==-1 || ans2==-1 || ans1>ans2){ans[que[i].id]=1;continue;}
        ans[que[i].id]=seg.query(max(ans2,0))-seg.query(max(ans1-1,0));
        if(ans[que[i].id]<1) ans[que[i].id]=1;
    }
    for(int i=1;i<=q;i++)
        cout<<ans[i]<<endl;
    return 0;
}