P13763 解题报告

前言

非常好的树上问题，使我的大脑旋转
不难，思维难度也不高，但是如果没有想到真的很难说

广告

同步发布于洛谷专栏，不确定有更好的阅读体验

题意

给出一颗树，不带边权点权，每次询问给出 \(s,t\) 问连接 \(s,t\) 后，有多少组 \((x,y)\) 满足 \(x\le y\) 并且 \(x,y\) 的距离变短了

思考

首先我们令我们给出的 \(dep_s>dep_t\)
那么首先 \(LCA_{s,t}\) 子树以外的节点之间不会产生任何贡献
所以贡献分为两种，一种都在 \(LCA\) 内部的贡献，另外一种是一个内部一个外部的贡献

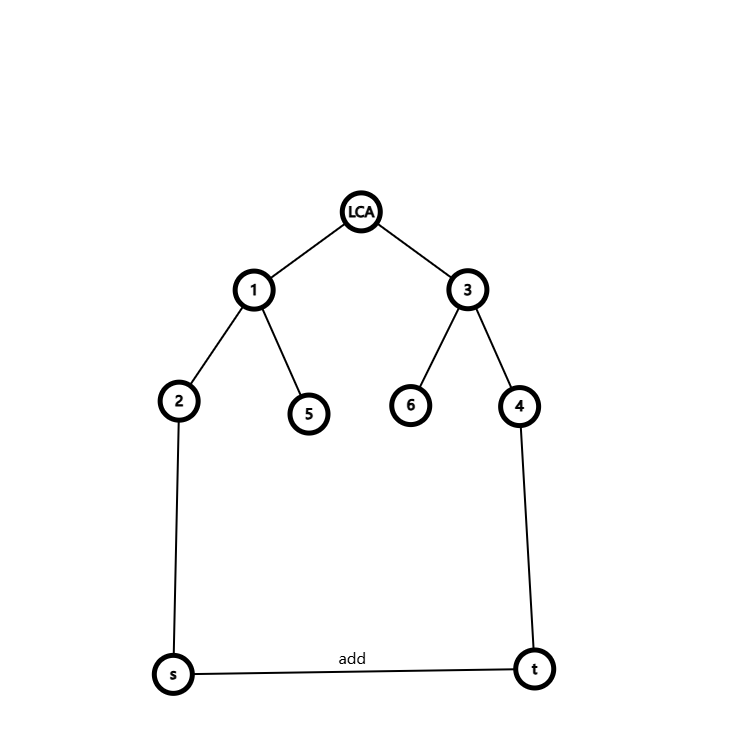
首先考虑都在内部的贡献
先手玩一下上面这个图，,发现 \((s,t),(s,3),(s,4)\) 都变短了，而且 \((s,6)\) 也变短了，进一步发现我们抽离出来 \(s\to t\) 的这个链，发现在这个链上面靠近 \(t\) 的节点的子树都能与 \(s\) 产生贡献，如果你在 \(s\) 下面加上一些节点，就会发现其实产生贡献的不止 \(s\) 而有 \(s\) 的子树。既然如此，我们考虑 \(s\) 的父亲的子树的贡献，为了防止产生重复的贡献，我们将 \(fa_s\) 的子树大小减去 \(siz_s\)，考虑一个在 \(fa_s\) 的子树里面的节点，他肯定是先走到 \(fa_s\) 然后走到 \(s\) 接着走到 \(s\to t\) 这个链上面的节点，玩一下发现链上面能和他产生贡献的节点相较于 \(s\) 向右移动了一位
所以我们可以将 \(s\to t\) 的链上的点抽离出来，然后将链之间的边删掉，然后每个点所在的连通块大小就是他能造成的贡献的大小，先求出 \(s\) 的贡献，然后每一次往后移一位就好了

做法

每一次将 \(s\to t\) 的链抽出来，记录每一个节点断开与链上两端的点的边所在连通块的大小，然后找到第一个无法与 \(s\) 产生贡献的位置，每一次向右移一位，然后记录后缀和统计答案即可。

代码

#include<algorithm>
#include<iostream>
#include<cstring>
#include<climits>
#include<vector>
#include<cmath>
#define ll long long

using namespace std;
const int N=1e6+9;
ll n,q,fa[N][26],dep[N],node[N*10],cnt,siz[N],nodesiz[N*10];
ll ans,hzsum[N*10];
vector<int>e[N];

inline void dfs(int x,int f){
    siz[x]=1;
    dep[x]=dep[f]+1;
    fa[x][0]=f;
    for(int i=1;i<=25;i++)
        fa[x][i]=fa[fa[x][i-1]][i-1];
    for(int to:e[x])
        if(to!=f)
            dfs(to,x),siz[x]+=siz[to];
}
inline int LCA(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=25;i>=0;i--)
        if(dep[fa[x][i]]>=dep[y])
            x=fa[x][i];
    if(x==y)return x;
    for(int i=25;i>=0;i--)
        if(fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
namespace IN {
    const int MAXX_INPUT = 1000000;
    #define getc() (p1 == p2 && (p2 = (p1 = buf) + inbuf -> sgetn(buf, MAXX_INPUT), p1 == p2) ? EOF : *p1++)
    char buf[MAXX_INPUT], *p1, *p2;
    template <typename T> inline bool redi(T &x) {
        static streambuf *inbuf = cin.rdbuf();
        x = 0;
        register int f = 0, flag = false;
        register char ch = getc();
        while (!isdigit(ch)) {
        	ch = getc();
        }
        if (isdigit(ch)) x = x * 10 + ch - '0', ch = getc(),flag = true;
        while (isdigit(ch)) {
            x = x * 10 + ch - 48;
            ch = getc();
        }
        return flag;
    }
    template <typename T,typename ...Args> inline bool redi(T& a,Args& ...args) {
       return redi(a) && redi(args...);
    }
    #undef getc
}
void write(ll x){
    if(x<0)putchar('-'),x=-x;
    if(x>9)write(x/10);
    putchar(x%10+'0');
    return;
}
using IN::redi;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    
    redi(n,q);
    for(int i=1;i<n;i++){
        int u,v;
        redi(u,v);
        e[u].push_back(v);
        e[v].push_back(u);
    }
    dfs(1,1);
    while(q--){
        ans=0;cnt=0;
        int s,t;
        redi(s,t);
        int lca=LCA(s,t);
        if(dep[s]<dep[t]) swap(s,t);
        int ns=s,nt=t;
        while(ns!=lca) node[++cnt]=ns,ns=fa[ns][0];
        node[++cnt]=lca;int tmpcnt=cnt;
        while(nt!=lca) node[++cnt]=nt,nt=fa[nt][0];
        reverse(node+tmpcnt+1,node+cnt+1);

        nodesiz[1]=siz[node[1]];
        for(int i=2;i<tmpcnt;i++)
            nodesiz[i]=siz[node[i]]-siz[node[i-1]];
        nodesiz[tmpcnt]=n-siz[node[tmpcnt-1]]-siz[node[tmpcnt+1]];
        for(int i=tmpcnt+1;i<cnt;i++)
            nodesiz[i]=siz[node[i]]-siz[node[i+1]];
        if(node[cnt]!=lca)nodesiz[cnt]=siz[node[cnt]];
        hzsum[cnt+1]=0;
        for(int i=cnt;i>=1;i--)hzsum[i]=hzsum[i+1]+nodesiz[i];

        int pos=0;
        for(int i=cnt;i>=0;i--){
            if(i-1<=cnt-i+1){
                pos=i;
                break;
            }
        }
        for(int i=1;i<=pos;i++){
            if(pos>=cnt) break;
            ans+=nodesiz[i]*hzsum[pos+1];
            pos++;
        }
        write(ans);puts("");

        for(int i=1;i<=cnt;i++)
            nodesiz[i]=0,hzsum[i]=0,node[i]=0;
    }
    return 0;
}