2025-7-30测试总结

前言

心态场时间问题
说一下排名和分数吧
100+30+20+15=165 斩获 rk.10
不够，至少出现了很多问题发现后肯定可以改进很多
后记的时候我在一一列举出来，这次的提升可能比较大，更多的是策略方面的问题而不是学习方面的，也算是技巧
而且自从这段时间打比赛开始时间就不太够用了，所以之前没有的顾虑现在要考虑一下了
剩下的后记说吧

题目

T1 因子

题目：给出一个序列要求求一个和最大的子序列要求他们有一个不为 \(1\) 的公约数。
做法：这题在考场过了不需要细讲所以我们直接过，对于每一个数字质因数分解后的每一个质数都 \(n\) 的时间复杂度求一遍就好。

T2 内鬼

题目：

一个 \(n\) 个点，\(m\) 个边的联通图，你可以给每个点染色，要求有 \(k\) 个黑色 \(n-k\) 个白色，如果一条边的两个点颜色不同你就可以走这条边，求是否存在一种染色方式使得现在的最短路比一开始的最短路长

思考：

这次的题目都是些什么鬼题面花里胡哨的干脆直接给形式化了
我会先把我在草稿纸上的方式写出来
我们首先发现对于一个图我们把它的最短路跑出来，那么我们就是要给这个图染色使得整张图不连通
但是我们发现这个题目只需要一个解即可，不需要最优解，赛事就卡在这里了
既然只需要一个解我们就只需要找出一个特殊解即可，那就去看 \(1,n\) 两个点
然后不妨假设他的最短路图长成这个样子

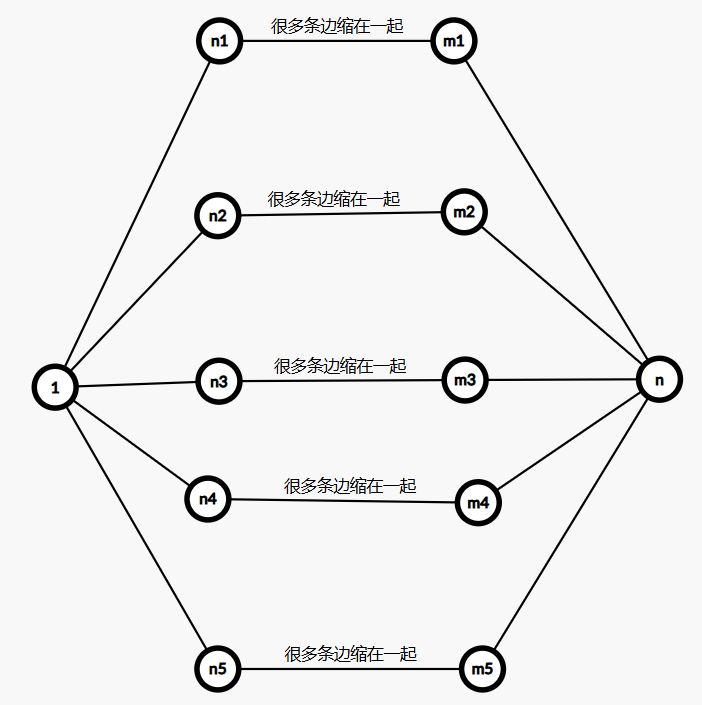
如果长成这个样子，那么我们可以让小 U 去霸占所有的 \(n_i\) 点，这个时候出现两种情况

• 1.如果霸占成功，也就是小 U 的点足够多，那么就说明我们可以让这些点之间不再联通
• 2.否则霸占失败，那么剩下的 \(m_i\) 都会被小 P 霸占，那么这样还是不连通

接着我们考虑一种情况，如果存在一个 \(n_i=m_i\) 那么此时只要 \(color_1 \neq color_n\)，我们发现安排小 U 去霸占和 \(1\) 联通的点，如果可以成功霸占，那么依旧不在联通，如果霸占失败，那么剩下的点会和 \(n\) 同色，这样会被切断他们与 \(n\) 的边，所以无论如何只要让小 U 去霸占 \(1\) 号点联通的点后剩下的交给小 P 就可以了。

思路：

总结一下就是对于和 \(1\) 联通的点放上 U 的壮丁，其他的放 P 的，除非 \(n=2,k=1\) 的情况盘不可能就可以了。

想法

第一个问题：写的时间太长了
这个题目在赛场上写了 2.5h 太长了严重导致了别的题目时间不够问题挺大的，同时 T1 想出来了赶紧写也挺重要的，这样才能给后面的题目预留足够的时间，因为写的时间太长了就没有去管后面的 T3 的更好的解法这里也会好好说一下。
第二个问题：想出来后过于犹豫
其实想出来之后赶紧写也挺重要的，不管怎么样，如果实在不想写去厕所清醒一下，也要磕出来，至少不能浪费太多时间，而且 T2 的要求是给出一组解而非最优解，显然如果中间的路径并在了一起是有更优解的，但是会发现，我们只需要考虑 \(1,n\) 两个特殊点即可，之后遇到如此的构造题不需要想最优，去从编号、度数、拓扑序等各种东西去考虑特殊点即可。

T3 异或序列

题意

给定 \(n,mod\)
求满足

• \(len\le n\)
• \(1\le a_i\le n\)
• \(a_i \lt a_{i+1} (i\lt len)\)
• \(a_i \oplus a_{i+1} \oplus a_{i+2} \neq 0\ (i\leq len-2)\)
  的序列数量对 \(mod\) 取模的值，使用 \(O(n\log_2n)\) 以内的时间复杂度

做法

这里只提供 @M_CI 的做法因为正确做法我不会
首先打表发现 \(ans_i=ans_{i-1}+k\) 把 \(k\) 列举出来，发现是

\[1,1,0,1,0,-4,-5,-85,-86,-90,-91,1,1,0,1,0,-4,-5,-85,-86,-90,-91,-21844,-21845... \]

然后发现其实 \(21045=85*(16*16+1)=5*(16+1)*(16*16+1)\) 然后规律就出来了

但是我其实想讲的是 DP,你可以设 \(dp_{i,j}\) 表示现在是 \(i\) 上一个是 \(j\) 第一维被滚掉了，这样的话可以 \(n^3\) 的转移，但是考场上没来得及写，这也是一个问题。

想法

收获第二大的题目
还是那个意思，想到了就去写！！

思考

这场考试其实可以考的更高的
这里就直接说我的问题：

• 1.时间安排不合理
• 2.思考的时候要仔细观察条件并且不过多犹豫
  之后没有犯过的话，连续三次不出现问题就可以不再记录了。