CF 1026 (Div.2) 5月24日 比赛总结

前言

记录时间：5月27日
这是这个 OIer 第 \(1\) 次比赛

其实考的不太理想，战绩是 \(3/6\)，如果仔细分析粗略估计可以达到 \(4/6\) 或者 \(5/6\)。
后期目标再追求 \(AK\)。

这次分析总计两个题目，为比赛的 \(C,D\) 三题，其中 \(C\) 做出来了，其余的那个没有。
然后直接进入我们的主题，开始分析薄弱部分。

C - racing

题目意思：类似于飞扬的小鸟，但是你不能下降。给你一个未定的 \(d_i\) 数组，有一些值已经确定，你需要确定所有 \(d_i\) 的值，满足对于所有的 \(s_i=\sum_{j=1}^i h_j\) 都有 \(l_i \le s_i \le r_i\)。
思路：做出来了，一笔带过。我们可以对于每一个点都记录一下我们最低的高度是多少（也就是所有的不定位置都填 \(0\)，并且满足我们这个点必须能飞过 \(l_i\)），和最高的高度是多少（最高和最低差不多，同理详见代码）然后最后记录答案时倒退即可。
评价：前三题 \(30\)min 必须解决，速度还要快点，但是下次目标必须是前四题，这个题目只是为了更多的推广。

D - Batteries

题目意思

给出一个有向无环带权图，每个点有一个点权 \(a_i\)，你需要给出一条路径，满足走过这条路径的每一条边的时候你的 \(sum \ge w_i\)，其中 \(w_i\) 是每条边的边权，你的 \(sum\) 在 \(v\) 号点时，你可以加上 \(0 \sim a_v\) 的任何值，你要保证到达终点时，你的 \(sum\) 最小。仅需要求出这个最小值。

为了帮助理解，我们可以分析一个样例：

4 4
3 10 0 0
1 2 1
1 3 3
2 3 10
3 4 5

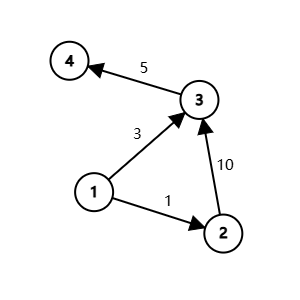
发现我们从 1 号点走到 3 号点，有两条路径，一种是直接走到 3，另一种则是走到 2 作为中转站，但是直接走到 3 只能带着最多 \(3\) 个电池，你走不到点 4，所以我们只能走 1 -> 2 -> 3 -> 4，尽管你必须带着 \(10\) 个电池。

答案为 \(10\)。

题目分析

首先先说考场思路，虽然没有想出来。

考场思路非常的板子，我们首先贪心一定是到一个点他的电池能少则少对吧，但是如果这个点的电池不够转移，但是如果前面全部拿满就可以转移的情况下，我们自然还需要记录一个最大值。

由此，我们完成了第一步，但是你会发现一个错误，就在我们分析的那个样例中，我们到到达三号点最少可以拿 3 个电池，最多 13 个，但是为什么答案是 \(10\) 而不是 \(5\) 呢？我们发现这个三号点虽然我们的数组记录的是 \(3\sim 13\) 个电池，实则只能拿到 \(3\sim 3\) 和 \(10 \sim 13\)，这是两个不同的区间，中间出现了一个 "真空区间"，这非常让我们反感，我们考虑解决这个恶心的问题。

在分析后我们发现如果我们的答案为 \(5\) 的话，我们就无法转移 2 -> 3的那一条边，这启发我们一个很重要的性质，二分，因为我们拿起了电池就无法放下，那么我们的每一条边就有可以转移和不可以转移的两种区别，然后我们发现如果 \(\le x\) 可以满足答案，\(\le x+1\) 也必然可以满足，所以我们考虑二分，check(x) 则是 \(\le x\) 个电池可以到 n 号点的可行性，发现这个东西二分后可以使用 DP 检验，DP 只需要满足尽可能的让我们的电池多带并且不超过 \(x\) 就可以了。

详细还是要看代码，如果还有不理解的可以去看 ANMMMMMM 的代码。

评价

最应当反思的一个题目。
为什么不能想到解决问题的方法？
可能是因为我对于这个题目没有什么思路，没有什么印象，也有可能是时间太晚不清醒然后没有什么更改的精神了。
但是总而言之，看出来了当我不知道这个题目用什么算法的时候，我没有一个明确的目标，比如 DP 优化可能需要使用什么算法或者做法都没有一个思路。而是只有一个数据结构，而没有更加深层次的考虑整个题目的目的与性质。
在此我需要提醒自己的是：我们分析问题的宏观方向是具有问题的，需要加强训练，同时二分的深层次理解与思考过程也需要加强。
这就是整个题目，后面的题目没有什么想法或者说没有深入思考，在此不作记录。