日志|搜索二维矩阵|搜索旋转排序数组|二分查找

力扣

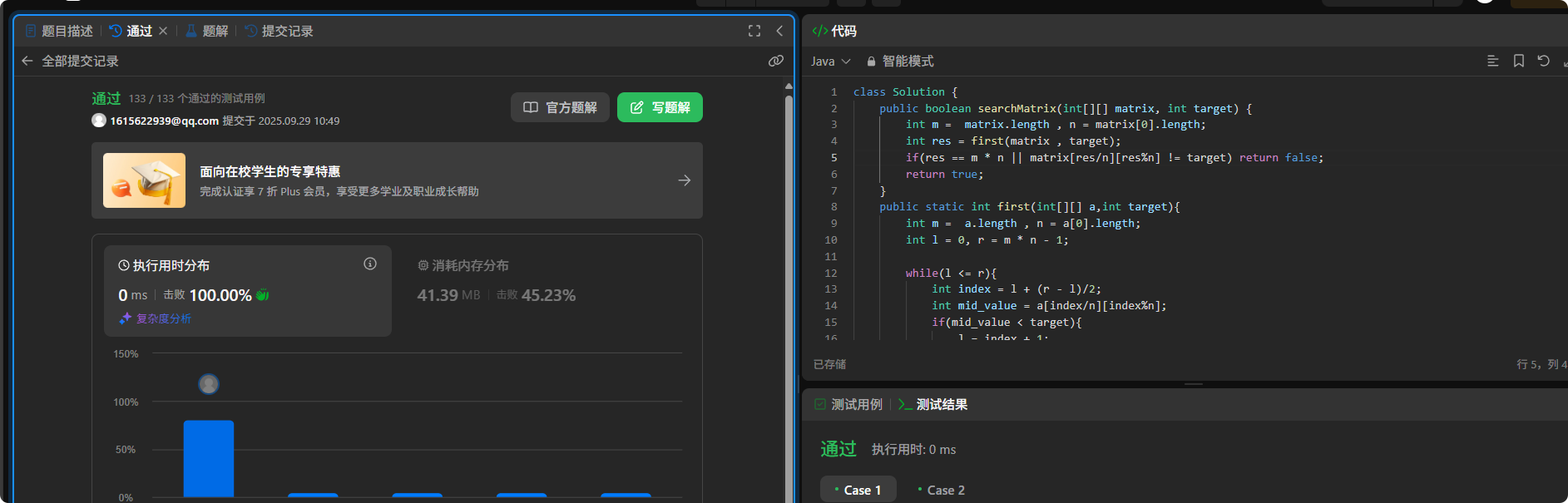
核心思路：一维数组中index对应矩阵中的索引公式=martix[index/n][index%n],掌握映射关系是关键。

点击查看代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m =  matrix.length , n = matrix[0].length;        
        int res = first(matrix , target);
        if(res == m * n || matrix[res/n][res%n] != target) return false;
        return true; 
    }
    public static int first(int[][] a,int target){
        int m =  a.length , n = a[0].length;
        int l = 0, r = m * n - 1;

        while(l <= r){
            int index = l + (r - l)/2;
            int mid_value = a[index/n][index%n];
            if(mid_value < target){
                l = index + 1;
            }
            else{
                r = index - 1;
            }
        }
        return l;
    }
}

点击查看代码

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) return -1;
        if (n == 1) return nums[0] == target ? 0 : -1;
        
        int pivot = findMinIndex(nums); // 找到旋转点（最小值索引）
        
        if (nums[pivot] == target) {
            return pivot;
        }
        
        // 根据目标值决定搜索区间
        int left, right;
        if (pivot == 0) {
            // 数组没有旋转，整个数组有序
            left = 0;
            right = n - 1;
        } else if (target >= nums[0]) {
            // 目标值在左半部分（从0到pivot-1）
            left = 0;
            right = pivot - 1;
        } else {
            // 目标值在右半部分（从pivot到末尾）
            left = pivot;
            right = n - 1;
        }
        
        // 标准二分查找
        return binarySearch(nums, target, left, right);
    }
    
    private int findMinIndex(int[] nums) {
        int left = 0, right = nums.length - 1;
        if (nums[left] < nums[right]) return 0; // 数组有序
        
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }
    
    private int binarySearch(int[] nums, int target, int left, int right) {
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;
    }
}