日志| 编辑距离 | 最长有效括号 |

力扣

解题思路

动态规划核心思想 ：初始化 + 填充

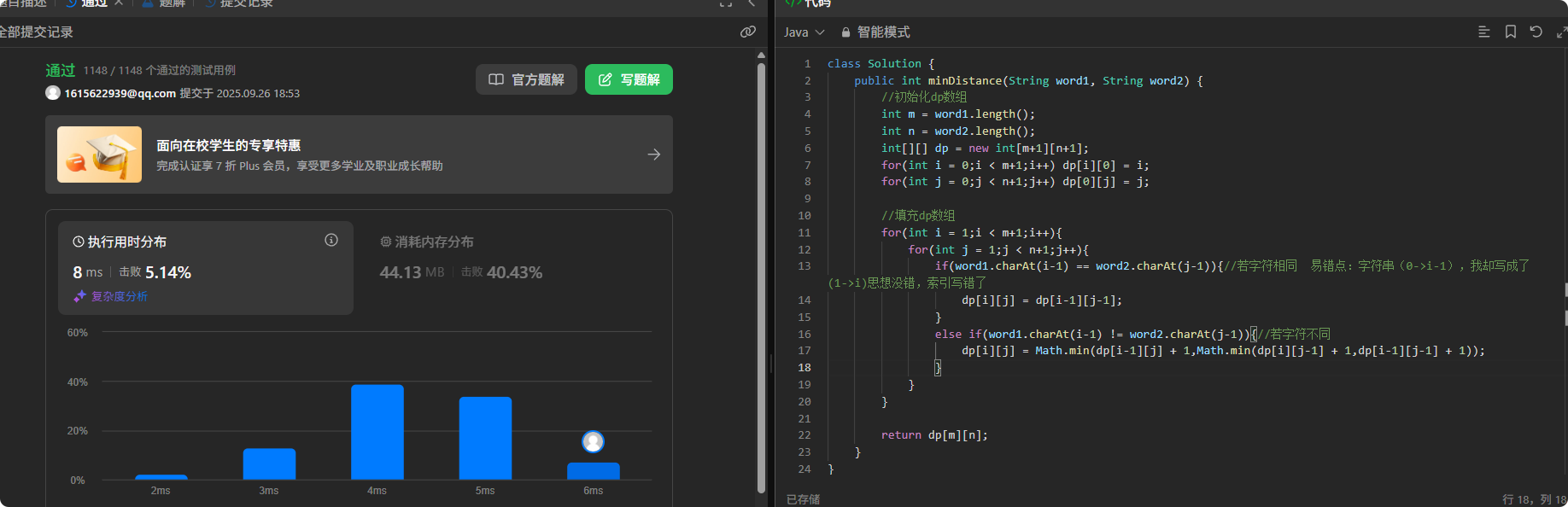
第一次提交
1状态转移:
左上到cur 是 替换(相同则继承左上)
上到cur 是 删除
左到cur 是 添加

2初始化：
第一行=空字符变成目标字符串的次数
第一列=原字符串变成空字符串的次数
3填充：
若 两字符相等 cur等于左上角
若 两字符不相等 cur等于(左上或者左或者上的最小值)+1

第二次提交
二维数组变成一维数组，每次只需要覆盖上一行的数组。
一层迭代需要记住 当前行的 左上角left_up 和 左边的第一个dp[0]
二层迭代需要记住 当前的dp[j] 是 下一个数的左上角

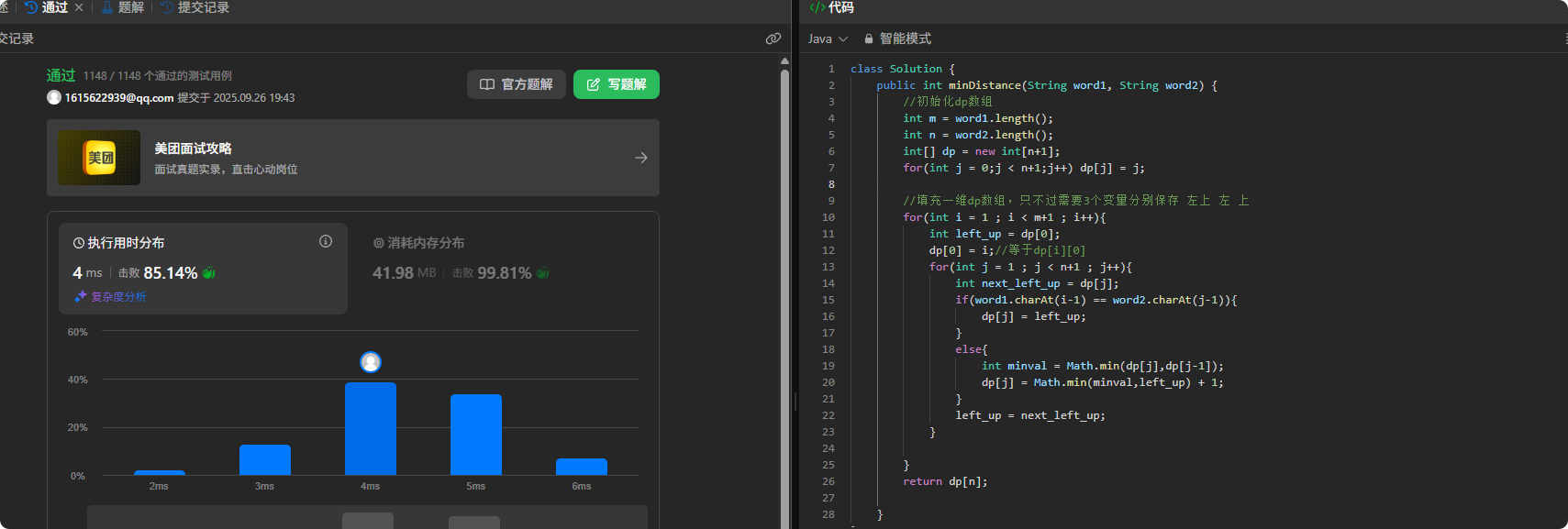
优化：
第一种方法空间复杂度度O（m * n）
第二种方法空间复杂度O(n)

解题思路

第一次提交
1创建boolean数组存储每个符号对应的TRUE OR FASLE
2遍历
若是左括号索引入栈
若是右括号检查并更新bool数组
3算一下最大长度

点击查看代码

class Solution {
    public int longestValidParentheses(String s) {
        if(s.length() == 0) return 0;
        int n = s.length();

        Stack<Integer> stack = new Stack<>();
        boolean[] test = new boolean[n];
        

        for(int i = 0 ; i < n ; i++){
            char cur = s.charAt(i);
            if(cur == '('){
                stack.push(i);
            }
            else{
                if(!stack.isEmpty()){
                    int a = stack.pop();
                    test[a] = true;
                    test[i] = true;
                }
            }
        }

        int maxLen = 0;
        int curmax = 0;

        for(int i = 0 ; i < n ; i++){
           
            if(test[i] == true){
                curmax += 1;
            }
            else{
                maxLen = Math.max(maxLen,curmax);
                curmax = 0;
            }
        }
        maxLen = Math.max(maxLen, curmax);//易错点：如果有小括号在末尾，会不更新最大值
        return maxLen;
    }
}