OO第二次博客作业
OO第二次博客作业
前言:
1、知识点总结:
① 字符串操作,正则表达式的训练及应用。
② 类与对象的设计,链表的实现,继承与多态,接口
2、题量:不多
3、难度分析:
题目集4:难在7-3 点线形系列3-三角形的计算:①判断输入的字符串格式是否正确②拆分字符串、提取字符串内容③直线切三角形的交点个数④分割后求两部分面积
题目集5:难在7-5 ATM机类结构设计(一)的框架整体设计
题目集6:难在7-2 点线形系列4-凸四边形的计算:①代码长度限制为25kb ②判断凸四边形是否按输入顺序(由于太难,本题没有考察凹四边形的输入顺序问题)③选项四(前两个点构成一条直线,后四个点构成一个四边形或三角形)对四点构成三角形的判断,求直线切四边形或三角形所得面积
源码设计与分析:
一、212016/71-题目集04——7-3 点线形系列3-三角形的计算
1.题目(如下图)

2.源码设计与分析:
本题肯定是要先判断输入的数据是否合法,再提取坐标,之后再去一个一个写选项,选项1~5基本就是数学问题
①拆分,提取坐标:使用indexOf()函数和substring()函数,还有字符串数组和循环( 具体见下面源码中splitDate(String date)函数 )
②判断单个字符串类型坐标的合法性( 具体见下面源码中dangehefa(String[] s)函数 )
③转换坐标数据为double型:使用parseDouble()函数
④开始写选项1~5:选项1~3很简单,难在选项4和5
选项4:使用状态法判断交点( 具体见下面源码中intersectionNumber_dividedArea(double[] z) )
(1)无交点:三点在一条直线的同侧(即同在直线的上下左右)
(2)1个交点:存在一点在线上,另外两点同侧
(3)2个交点:存在一点与另外两点异侧
求面积:大三角形减小三角形
选项5:不会射线法,使用同向法( 具体见下面源码中isInsideTriangle(double[] z) )
设三角形内有一点O,则向量AO是夹在向量AB和向量AC中的,即向量AB叉乘向量AO的结果的方向与向量AO叉乘向量AC的结果的方向不同
根据顶点的不同有三种情况,同时满足则在三角形内
3.源码(很长,已折叠,记得点加号打开)
 7-3 点线形系列3-三角形的
7-3 点线形系列3-三角形的4.踩坑心得
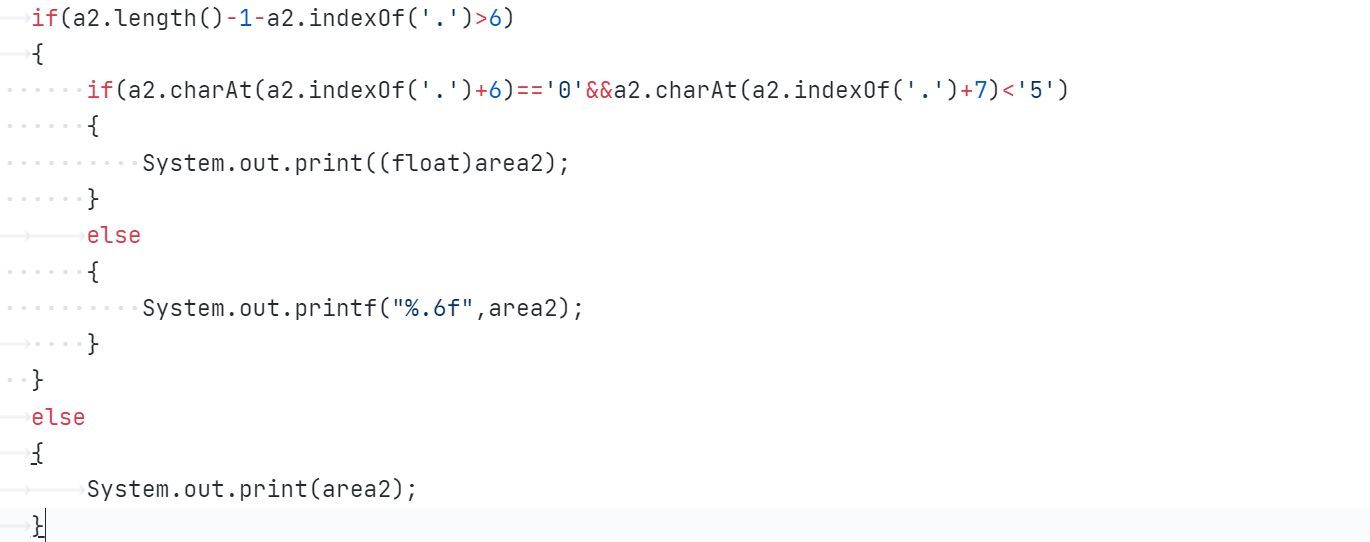
①输出的格式
![]()
下面的方法我也是想了很久
②尽量多写点方法,否则出现bug非常恐怖,我其中好几个bug都找了好几个小时
如这样的数据就很不可取

5.改进建议(写完题目集6后发现)千万不能像本题源码这样写
①判断字符串数据格式和提取坐标可以用正则表达式,非常简便,值得一学
②除主类外,可以增加两个类,一个是点类,一个是线类,在这两个类中添加很多方法(如求斜率,两点长度,点与线的位置等方法),
之后在主类中为选项写方法会非常简单,如本题两三百多行的代码用三四十行就可写完(如·直线切三角形求交点求面积那部分)
具体见下面一题
二、212016/71-题目集06——7-2 点线形系列4-凸四边形的计算
1.题目(如下图)

2.源码设计与分析:
除主类外,可以增加两个类,一个是点类,一个是线类,在这两个类中添加很多方法(如求斜率,两点长度,点与线的位置等方法),
之后在主类中为选项写方法会非常简单
①类图:由于类中方法太多,在此类间线条就去掉了
主类 点类 线类
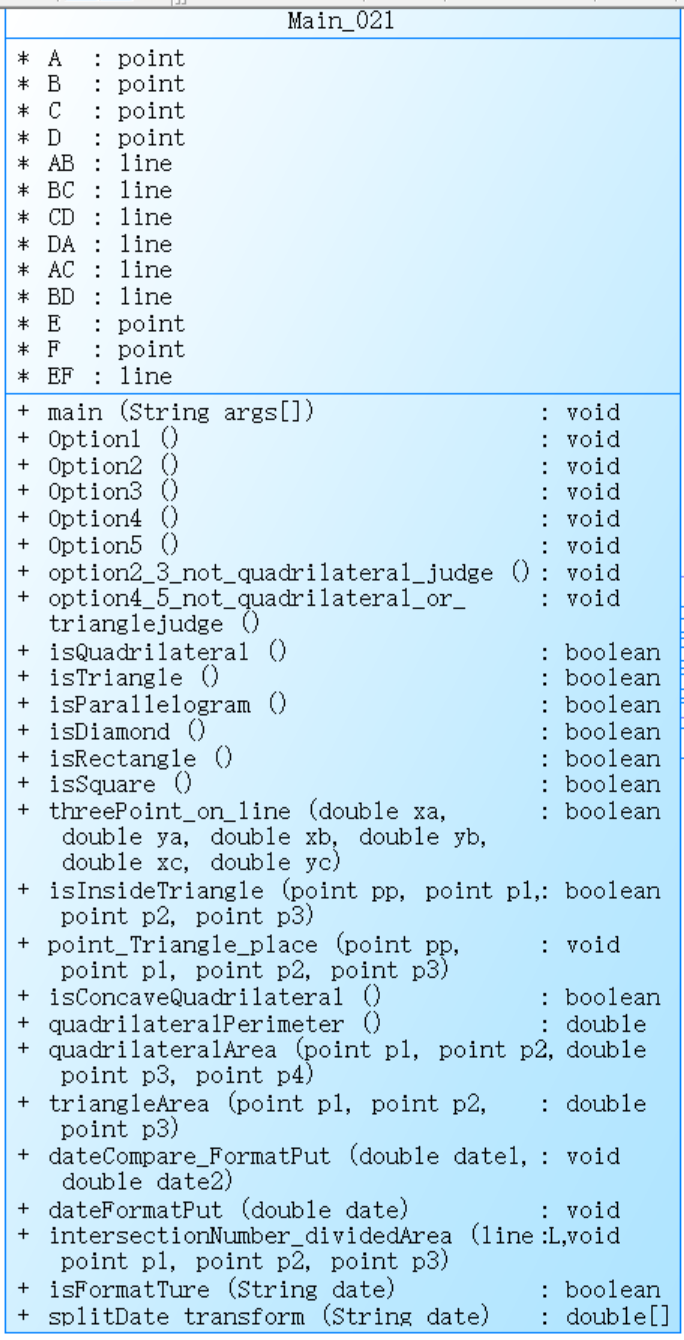
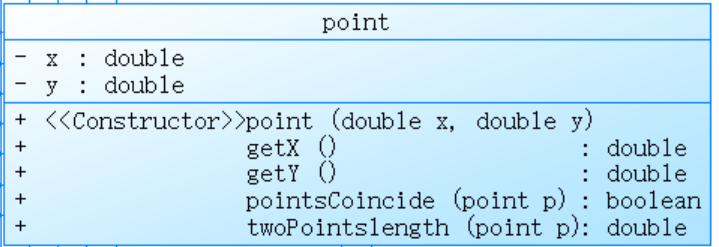
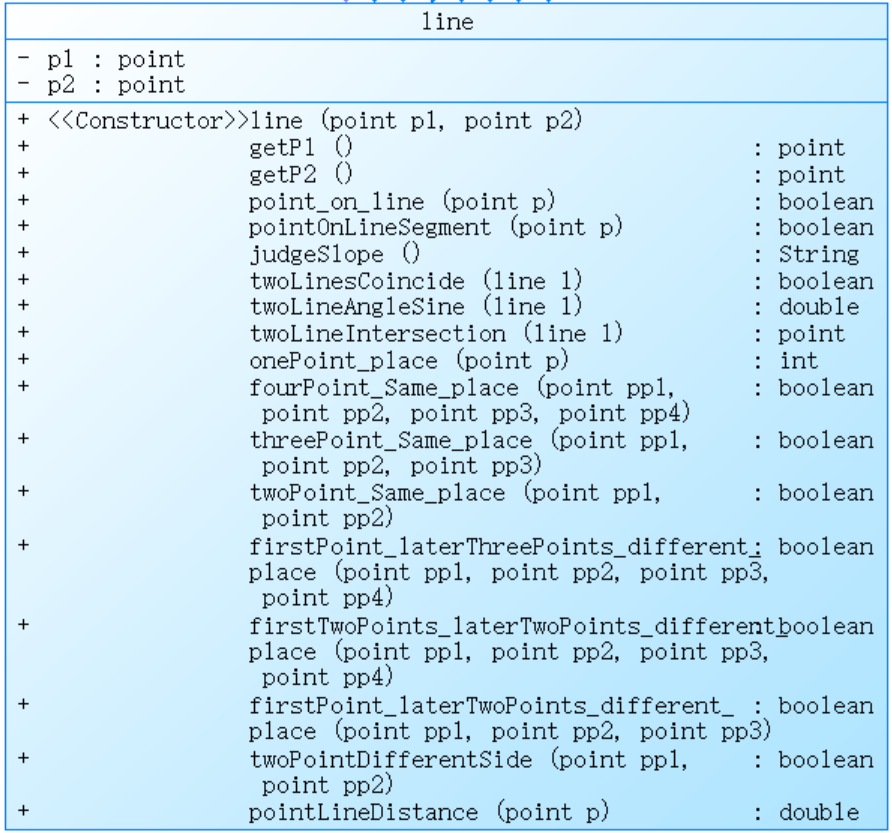
②使用正则表达式判断输入格式:String regex = "[1-5]:((\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*),(\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*) )*
((\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*),(\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*)( )?)+";
③提取坐标数据: Pattern pattern = Pattern.compile("(-?\\d*)\\.?\\d+"); //创建个匹配器
④选项5:点在四边形内,即只要点在由四边形四个顶点构成其中四个三角形中的一个就是在四边形内,当然也可以在对角线上(不含顶点)
⑤其他可以参照源码,有每个方法的作用的注释,应该很容易理解
3.源码(很长,已折叠,记得点加号打开)

1 import java.util.Scanner; 2 import java.util.regex.Matcher; 3 import java.util.regex.Pattern; 4 public class Main { 5 static point A;static point B;static point C;static point D;static line AB;static line BC;static line CD;static line DA;static line AC;static line BD;static point E;static point F;static line EF; 6 public static void main(String[] args) { 7 // TODO Auto-generated method stub 8 Scanner in = new Scanner(System.in); 9 String date = in.nextLine(); 10 if(!isFormatTure(date)){ 11 System.out.println("Wrong Format"); 12 System.exit(0); 13 } 14 double[] array = splitDate_transform(date); 15 if(!(((date.charAt(0)=='1'||date.charAt(0)=='2'||date.charAt(0)=='3')&&array.length==8)||(date.charAt(0)=='4'&&array.length==12)||(date.charAt(0)=='5'&&array.length==10))){ 16 System.out.println("wrong number of points"); 17 System.exit(0); 18 } 19 if(date.charAt(0)=='1'||date.charAt(0)=='2'||date.charAt(0)=='3') { 20 A = new point(array[0], array[1]);B = new point(array[2], array[3]);C = new point(array[4], array[5]);D = new point(array[6], array[7]); 21 AB = new line(A, B);BC = new line(B, C);CD = new line(C, D);DA = new line(D, A);AC = new line(A, C);BD = new line(B, D); 22 if(date.charAt(0)=='1') { 23 if(A.pointsCoincide(B)||A.pointsCoincide(C)||A.pointsCoincide(D)||B.pointsCoincide(C)||B.pointsCoincide(D)||C.pointsCoincide(D)) { 24 System.out.println("points coincide"); 25 System.exit(0); 26 } 27 Option1();} 28 if(date.charAt(0)=='2') { 29 option2_3_not_quadrilateral_judge(); 30 Option2();} 31 if(date.charAt(0)=='3') { 32 option2_3_not_quadrilateral_judge(); 33 Option3();} 34 }else if(date.charAt(0)=='4'){ 35 A = new point(array[4], array[5]);B = new point(array[6], array[7]);C = new point(array[8], array[9]);D = new point(array[10], array[11]);E = new point(array[0], array[1]);F = new point(array[2], array[3]); 36 AB = new line(A, B);BC = new line(B, C);CD = new line(C, D);DA = new line(D, A);AC = new line(A, C);BD = new line(B, D);EF = new line(E, F); 37 if(E.pointsCoincide(F)) { 38 System.out.println("points coincide"); 39 System.exit(0); 40 } 41 option4_5_not_quadrilateral_or_trianglejudge(); 42 Option4(); 43 }else if(date.charAt(0)=='5'){ 44 A = new point(array[2], array[3]);B = new point(array[4], array[5]);C = new point(array[6], array[7]);D = new point(array[8], array[9]);E = new point(array[0], array[1]); 45 AB = new line(A, B);BC = new line(B, C);CD = new line(C, D);DA = new line(D, A);AC = new line(A, C);BD = new line(B, D); 46 option4_5_not_quadrilateral_or_trianglejudge(); 47 Option5(); 48 } 49 } 50 public static void Option1() { 51 System.out.println(isQuadrilateral()+" "+isParallelogram()); 52 } 53 public static void Option2() { 54 System.out.println(isDiamond()+" "+isRectangle()+" "+isSquare()); 55 } 56 public static void Option3() { 57 System.out.print(!isConcaveQuadrilateral()+" ");dateFormatPut(quadrilateralPerimeter());System.out.print(" ");dateFormatPut(quadrilateralArea(A, B, C, D)); 58 } 59 public static void Option4() { 60 if(BD.pointOnLineSegment(A)&&!BD.point_on_line(C)) {//三角形 61 intersectionNumber_dividedArea(EF,B,D,C ); 62 }else if(AC.pointOnLineSegment(B)&&!AC.point_on_line(D)) { 63 intersectionNumber_dividedArea(EF,A,C,D ); 64 }else if(BD.pointOnLineSegment(C)&&!BD.point_on_line(A)) { 65 intersectionNumber_dividedArea(EF,B,D,A ); 66 }else if(AC.pointOnLineSegment(D)&&!AC.point_on_line(B)) { 67 intersectionNumber_dividedArea(EF,A,C,B ); 68 }else if( !B.pointsCoincide(D)&&!BD.point_on_line(A)&&!BD.point_on_line(C)&&A.pointsCoincide(C) ) { 69 intersectionNumber_dividedArea(EF,A,B,D ); 70 }else if( !A.pointsCoincide(C)&&!AC.point_on_line(B)&&!AC.point_on_line(D)&&B.pointsCoincide(D) ) { 71 intersectionNumber_dividedArea(EF,B,A,C ); 72 } 73 74 if(isQuadrilateral()&&!isConcaveQuadrilateral()) {//凸四边形 75 if(EF.twoLinesCoincide(AB)||EF.twoLinesCoincide(BC)||EF.twoLinesCoincide(CD)||EF.twoLinesCoincide(DA)) { 76 System.out.println("The line is coincide with one of the lines"); 77 System.exit(0); 78 } 79 if( EF.fourPoint_Same_place(A, B, C, D) ) {//无交点 80 System.out.println(0); 81 }else if( ( EF.point_on_line(A)&&EF.threePoint_Same_place(B, C, D) )|| ( EF.point_on_line(B)&&EF.threePoint_Same_place(A, C, D) )||( EF.point_on_line(C)&&EF.threePoint_Same_place(A, B, D) )||( EF.point_on_line(D)&&EF.threePoint_Same_place( A, B, C) ) ){//一个交点 82 System.out.println(1); 83 }else if( EF.firstPoint_laterThreePoints_different_place(A, B, C, D) ) {//两个交点 84 dateCompare_FormatPut( triangleArea(A, EF.twoLineIntersection(AB), EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-triangleArea(A, EF.twoLineIntersection(AB), EF.twoLineIntersection(DA) ) ); 85 }else if( EF.firstPoint_laterThreePoints_different_place(B, A, C, D) ) { 86 dateCompare_FormatPut( triangleArea(B, EF.twoLineIntersection(AB), EF.twoLineIntersection(BC) ), quadrilateralArea(A, B, C, D)-triangleArea(B, EF.twoLineIntersection(AB), EF.twoLineIntersection(BC) ) ); 87 }else if( EF.firstPoint_laterThreePoints_different_place(C, A, B, D) ) { 88 dateCompare_FormatPut( triangleArea(C, EF.twoLineIntersection(BC), EF.twoLineIntersection(CD) ), quadrilateralArea(A, B, C, D)-triangleArea(C, EF.twoLineIntersection(BC), EF.twoLineIntersection(CD) ) ); 89 }else if( EF.firstPoint_laterThreePoints_different_place(D, A, B, C) ) { 90 dateCompare_FormatPut( triangleArea(D, EF.twoLineIntersection(CD), EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-triangleArea(D, EF.twoLineIntersection(CD), EF.twoLineIntersection(DA) ) ); 91 }else if( EF.point_on_line(A)&&EF.point_on_line(C) ) { 92 dateCompare_FormatPut( triangleArea(A, B, C), triangleArea(A, D, C)); 93 }else if( EF.point_on_line(B)&&EF.point_on_line(D) ) { 94 dateCompare_FormatPut( triangleArea(A, B, D), triangleArea(C, B, D)); 95 }else if( EF.firstTwoPoints_laterTwoPoints_different_place(A, B, C, D) ) { 96 dateCompare_FormatPut( quadrilateralArea(A, B, EF.twoLineIntersection(AB), EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-quadrilateralArea(A, B,EF.twoLineIntersection(AB), EF.twoLineIntersection(DA) ) ); 97 }else if( EF.firstTwoPoints_laterTwoPoints_different_place(B, C, D, A) ) { 98 dateCompare_FormatPut( quadrilateralArea(B, C, EF.twoLineIntersection(CD), EF.twoLineIntersection(AB) ), quadrilateralArea(A, B, C, D)-quadrilateralArea(B, C, EF.twoLineIntersection(CD), EF.twoLineIntersection(AB) ) ); 99 } 100 } 101 else if(isConcaveQuadrilateral()) {//凹四边形 102 if( EF.fourPoint_Same_place(A, B, C, D) ) {//无交点 103 System.out.println(0); 104 }else if( ( ( isInsideTriangle(B, A, C, D) || isInsideTriangle(C, A, B, D) || isInsideTriangle(D, A, B, C) ) && EF.point_on_line(A)&&EF.threePoint_Same_place(B, C, D) ) || ( ( isInsideTriangle(A, B, C, D) || isInsideTriangle(C, A, B, D) || isInsideTriangle(D, A, B, C) ) && EF.point_on_line(B)&&EF.threePoint_Same_place(A, C, D) ) || ( ( isInsideTriangle(A, B, C, D) || isInsideTriangle(B, A, C, D) || isInsideTriangle(D, A, B, C) ) && EF.point_on_line(C)&&EF.threePoint_Same_place(A, B, D) ) || ( ( isInsideTriangle(A, B, C, D) || isInsideTriangle(B, A, C, D) || isInsideTriangle(C, A, B, D) ) && EF.point_on_line(D)&&EF.threePoint_Same_place(A, B, C) ) ) {//一个交点 105 System.out.println(1); 106 }else if( ( isInsideTriangle(B, A, C, D) || isInsideTriangle(C, A, B, D) || isInsideTriangle(D, A, B, C) ) && EF.firstPoint_laterThreePoints_different_place(A, B, C, D) ) {//两个交点 107 dateCompare_FormatPut( triangleArea(A, EF.twoLineIntersection(AB), EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-triangleArea(A, EF.twoLineIntersection(AB), EF.twoLineIntersection(DA) ) ); 108 }else if( ( isInsideTriangle(A, B, C, D) || isInsideTriangle(C, A, B, D) || isInsideTriangle(D, A, B, C) ) && EF.firstPoint_laterThreePoints_different_place(B, A, C, D) ) {//两个交点 109 dateCompare_FormatPut( triangleArea(B, EF.twoLineIntersection(AB), EF.twoLineIntersection(BC) ), quadrilateralArea(A, B, C, D)-triangleArea(B, EF.twoLineIntersection(AB), EF.twoLineIntersection(BC) ) ); 110 }else if( ( isInsideTriangle(A, B, C, D) || isInsideTriangle(B, A, C, D) || isInsideTriangle(D, A, B, C) ) && EF.firstPoint_laterThreePoints_different_place(C, A, B, D) ) {//两个交点 111 dateCompare_FormatPut( triangleArea(C, EF.twoLineIntersection(BC), EF.twoLineIntersection(CD) ), quadrilateralArea(A, B, C, D)-triangleArea(C, EF.twoLineIntersection(BC), EF.twoLineIntersection(CD) ) ); 112 }else if( ( isInsideTriangle(A, B, C, D) || isInsideTriangle(B, A, C, D) || isInsideTriangle(C, A, B, D) ) && EF.firstPoint_laterThreePoints_different_place(D, A, B, C) ) {//两个交点 113 dateCompare_FormatPut( triangleArea(D, EF.twoLineIntersection(CD), EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-triangleArea(D, EF.twoLineIntersection(CD), EF.twoLineIntersection(DA) ) ); 114 }else if( ( isInsideTriangle(A, B, C, D)||isInsideTriangle(C, A, B, D) ) && EF.point_on_line(A)&&EF.point_on_line(C) ) {//两个交点 115 dateCompare_FormatPut( triangleArea(A, B, C), triangleArea(A, D, C)); 116 }else if( ( isInsideTriangle(A, B, C, D)||isInsideTriangle(C, A, B, D) ) && EF.point_on_line(B)&&EF.point_on_line(D) ) {//两个交点 117 System.out.print(2+" "+0+" ");dateFormatPut(quadrilateralArea(A, B, C, D)); 118 }else if( ( isInsideTriangle(B, A, C, D)||isInsideTriangle(D, A, B, C) ) && EF.point_on_line(A)&&EF.point_on_line(C) ) {//两个交点 119 System.out.print(2+" "+0+" ");dateFormatPut(quadrilateralArea(A, B, C, D)); 120 }else if( ( isInsideTriangle(B, A, C, D)||isInsideTriangle(D, A, B, C) ) && EF.point_on_line(B)&&EF.point_on_line(D) ) {//两个交点 121 dateCompare_FormatPut( triangleArea(A, B, D), triangleArea(C, B, D)); 122 }else if( EF.point_on_line(A)&&EF.firstPoint_laterTwoPoints_different_place(B, C, D) ) {//两个交点 123 dateCompare_FormatPut( triangleArea(B, A, EF.twoLineIntersection(BC) ), quadrilateralArea(A, B, C, D)-triangleArea(B, A, EF.twoLineIntersection(BC) ) ); 124 }else if( EF.point_on_line(A)&&EF.firstPoint_laterTwoPoints_different_place(D, B, C) ) {//两个交点 125 dateCompare_FormatPut( triangleArea(D, A, EF.twoLineIntersection(CD) ), quadrilateralArea(A, B, C, D)-triangleArea(D, A, EF.twoLineIntersection(CD) ) ); 126 }else if( EF.point_on_line(B)&&EF.firstPoint_laterTwoPoints_different_place(A, C, D) ) {//两个交点 127 dateCompare_FormatPut( triangleArea(A, B, EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-triangleArea(A, B, EF.twoLineIntersection(DA) ) ); 128 }else if( EF.point_on_line(B)&&EF.firstPoint_laterTwoPoints_different_place(C, A, D) ) {//两个交点 129 dateCompare_FormatPut( triangleArea(C, B, EF.twoLineIntersection(CD) ), quadrilateralArea(A, B, C, D)-triangleArea(C, B, EF.twoLineIntersection(CD) ) ); 130 }else if( ( EF.point_on_line(C)&&EF.firstPoint_laterTwoPoints_different_place(B, A, D) ) ) {//两个交点 131 dateCompare_FormatPut( triangleArea(B, C, EF.twoLineIntersection(AB) ), quadrilateralArea(A, B, C, D)-triangleArea(B, C, EF.twoLineIntersection(AB) ) ); 132 }else if( ( EF.point_on_line(C)&&EF.firstPoint_laterTwoPoints_different_place(D, A, B) ) ) {//两个交点 133 dateCompare_FormatPut( triangleArea(D, C, EF.twoLineIntersection(DA) ), quadrilateralArea(A, B, C, D)-triangleArea(D, C, EF.twoLineIntersection(DA) ) ); 134 }else if( ( EF.point_on_line(D)&&EF.firstPoint_laterTwoPoints_different_place(A, B, C) ) ) {//两个交点 135 dateCompare_FormatPut( triangleArea(A, D, EF.twoLineIntersection(AB) ), quadrilateralArea(A, B, C, D)-triangleArea(A, D, EF.twoLineIntersection(AB) ) ); 136 }else if( ( EF.point_on_line(D)&&EF.firstPoint_laterTwoPoints_different_place(C, A, B) ) ) {//两个交点 137 dateCompare_FormatPut( triangleArea(C, D, EF.twoLineIntersection(BC) ), quadrilateralArea(A, B, C, D)-triangleArea(C, D, EF.twoLineIntersection(BC) ) ); 138 }else if( ( isInsideTriangle(A, B, C, D)&&EF.point_on_line(A)&&EF.firstPoint_laterTwoPoints_different_place(C, B, D) ) || ( isInsideTriangle(B, A, C, D)&&EF.point_on_line(B)&&EF.firstPoint_laterTwoPoints_different_place(D, A, C) ) || ( isInsideTriangle(C, A, B, D)&&EF.point_on_line(C)&&EF.firstPoint_laterTwoPoints_different_place(A, B, D) ) || ( isInsideTriangle(D, A, B, C)&&EF.point_on_line(D)&&EF.firstPoint_laterTwoPoints_different_place(B, A, C) ) 139 || ( (isInsideTriangle(A, B, C, D)||isInsideTriangle(C, A, B, D))&&( ( EF.point_on_line(B)&&EF.firstPoint_laterTwoPoints_different_place(D, A, C) ) || ( EF.point_on_line(D)&&EF.firstPoint_laterTwoPoints_different_place(B, A, C) ) ) ) 140 || ( (isInsideTriangle(B, A, C, D)||isInsideTriangle(D, A, B, C))&&( ( EF.point_on_line(A)&&EF.firstPoint_laterTwoPoints_different_place(C, B, D) ) || ( EF.point_on_line(C)&&EF.firstPoint_laterTwoPoints_different_place(A, B, D) ) ) ) 141 ) {//三个交点 142 System.out.println(3); 143 }else if( EF.firstTwoPoints_laterTwoPoints_different_place(A, C, B, D) ) {//四个交点 144 System.out.println(4); 145 } 146 } 147 } 148 public static void Option5() { 149 if(isTriangle()) { 150 if(BD.pointOnLineSegment(A)&&!BD.point_on_line(C)) { 151 point_Triangle_place(E,B,D,C ); 152 }else if(AC.pointOnLineSegment(B)&&!AC.point_on_line(D)) { 153 point_Triangle_place(E,A,C,D ); 154 }else if(BD.pointOnLineSegment(C)&&!BD.point_on_line(A)) { 155 point_Triangle_place(E,B,D,A ); 156 }else if(AC.pointOnLineSegment(D)&&!AC.point_on_line(B)) { 157 point_Triangle_place(E,A,C,B ); 158 } 159 } 160 if(isQuadrilateral()&&!isConcaveQuadrilateral()){ 161 if(isInsideTriangle(E,A,B,C)||isInsideTriangle(E,A,B,D)||isInsideTriangle(E,A,C,D)||isInsideTriangle(E,B,C,D)) { 162 System.out.println("in the quadrilateral"); 163 }else { 164 if(AB.pointOnLineSegment(E)||BC.pointOnLineSegment(E)||CD.pointOnLineSegment(E)||DA.pointOnLineSegment(E)) { 165 System.out.println("on the quadrilateral"); 166 }else if(AC.pointOnLineSegment(E)||BD.pointOnLineSegment(E)) { 167 System.out.println("in the quadrilateral"); 168 }else { 169 System.out.println("outof the quadrilateral"); 170 } 171 } 172 } 173 } 174 public static void option2_3_not_quadrilateral_judge(){ 175 if( A.pointsCoincide(B)||A.pointsCoincide(C)||A.pointsCoincide(D)||B.pointsCoincide(C)||B.pointsCoincide(D)||C.pointsCoincide(D) 176 ||!isQuadrilateral() ) { 177 System.out.println("not a quadrilateral"); 178 System.exit(0); 179 } } 180 public static void option4_5_not_quadrilateral_or_trianglejudge(){ 181 if(!isQuadrilateral()&&!isTriangle()) { 182 System.out.println("not a quadrilateral or triangle"); 183 System.exit(0); 184 } } 185 //判断是否为四边形 186 public static boolean isQuadrilateral() { 187 return !AB.point_on_line(C)&&!AB.point_on_line(D)&&!BC.point_on_line(A)&&!BC.point_on_line(D)&&!CD.point_on_line(B)&&!CD.point_on_line(A)&&!DA.point_on_line(B)&&!DA.point_on_line(C) 188 &&( ( AC.twoPointDifferentSide(B, D)&&BD.twoPointDifferentSide(A, C)&&!isConcaveQuadrilateral())|| isConcaveQuadrilateral()); 189 } 190 //判断四点是否构成为三角形 191 public static boolean isTriangle() { 192 return ( !B.pointsCoincide(D)&&!BD.point_on_line(A)&&!BD.point_on_line(C)&&A.pointsCoincide(C) ) 193 || ( !A.pointsCoincide(C)&&!AC.point_on_line(B)&&!AC.point_on_line(D)&&B.pointsCoincide(D) ) 194 || ( !B.pointsCoincide(D)&&BD.pointOnLineSegment(A)&&!BD.point_on_line(C) ) 195 || ( !A.pointsCoincide(C)&&AC.pointOnLineSegment(B)&&!AC.point_on_line(D) ) 196 || ( !B.pointsCoincide(D)&&BD.pointOnLineSegment(C)&&!BD.point_on_line(A) ) 197 || ( !A.pointsCoincide(C)&&AC.pointOnLineSegment(D)&&!AC.point_on_line(B) ) ; 198 } 199 //判断是否为平行四边形 200 public static boolean isParallelogram() { 201 return isQuadrilateral()&&AB.judgeSlope().equals(CD.judgeSlope())&&A.twoPointslength(B)==C.twoPointslength(D)&&BC.judgeSlope().equals(DA.judgeSlope())&&B.twoPointslength(C)==D.twoPointslength(A); 202 } 203 //判断是否为菱形 204 public static boolean isDiamond() { 205 return isParallelogram()&&A.twoPointslength(B)==B.twoPointslength(C); 206 } 207 //判断是否为矩形 208 public static boolean isRectangle() { 209 return isParallelogram()&&A.twoPointslength(C)==B.twoPointslength(D); 210 } 211 //判断是否为正方形 212 public static boolean isSquare() { 213 return isDiamond()&&A.twoPointslength(C)==B.twoPointslength(D); 214 } 215 //三点共线 216 public static boolean threePoint_on_line(double xa, double ya, double xb, double yb, double xc, double yc) { 217 return (ya-yb)*xc-(xa-xb)*yc+xa*yb-xb*ya==0; 218 } 219 //判断点是否在三角形内 220 public static boolean isInsideTriangle(point pp, point p1, point p2, point p3) { 221 double xp = pp.getX(), yp = pp.getY(), xa = p1.getX(), ya = p1.getY(), xb = p2.getX(), yb = p2.getY(), xc = p3.getX(), yc = p3.getY(); 222 if(threePoint_on_line(xa,ya,xb,yb,xc,yc)) { 223 return false; 224 } 225 double mixedProduct_c=( (xa-xp)*(yb-ya)-(xb-xa)*(ya-yp) )*( (xa-xc)*(yb-ya)-(xb-xa)*(ya-yc) ); 226 double mixedProduct_a=( (xb-xp)*(yc-yb)-(xc-xb)*(yb-yp) )*( (xb-xa)*(yc-ya)-(xc-xb)*(yb-ya) ); 227 double mixedProduct_b=( (xc-xp)*(ya-yc)-(xa-xc)*(yc-yp) )*( (xc-xb)*(ya-yc)-(xa-xc)*(yc-yb) ); 228 if(mixedProduct_c>0&&mixedProduct_a>0&&mixedProduct_b>0){ 229 return true; 230 }else{ 231 return false; 232 } 233 } 234 //判断点在三角形内、外、上 235 public static void point_Triangle_place(point pp, point p1,point p2,point p3) { 236 line l12 = new line(p1, p2);line l23 = new line(p2, p3);line l13 = new line(p1, p3); 237 if(l12.pointOnLineSegment(pp)||l23.pointOnLineSegment(pp)||l13.pointOnLineSegment(pp)) { 238 System.out.println("on the triangle"); 239 }else if(isInsideTriangle(pp, p1, p2 ,p3)) { 240 System.out.println("in the triangle"); 241 }else { 242 System.out.println("outof the triangle"); 243 } 244 } 245 //判断是否为凹四边形 246 public static boolean isConcaveQuadrilateral() { 247 return isInsideTriangle(A, B, C, D)||isInsideTriangle(B, A, C, D)||isInsideTriangle(C, B, A, D)||isInsideTriangle(D, B, C, A) ; 248 } 249 //求四边形周长 250 public static double quadrilateralPerimeter() { 251 return A.twoPointslength(B)+B.twoPointslength(C)+C.twoPointslength(D)+D.twoPointslength(A); 252 } 253 //求四边形面积 254 public static double quadrilateralArea(point p1, point p2, point p3, point p4) { 255 line l1 = new line(p1, p3);line l2 = new line(p2, p4); 256 return p1.twoPointslength(p3)*p2.twoPointslength(p4)*l1.twoLineAngleSine(l2)/2.0; 257 } 258 //求三角形面积 259 public static double triangleArea(point p1, point p2,point p3) { 260 double s = (p1.twoPointslength(p2)+p1.twoPointslength(p3)+p2.twoPointslength(p3))/2.0; 261 return Math.sqrt(s*(s-p1.twoPointslength(p2))*(s-p1.twoPointslength(p3))*(s-p2.twoPointslength(p3))); 262 } 263 //数据比较后格式输出 264 public static void dateCompare_FormatPut(double date1, double date2) { 265 System.out.print(2+" "); 266 if(date1<date2) { 267 dateFormatPut(date1);System.out.printf(" ");dateFormatPut(date2); 268 }else { 269 dateFormatPut(date2);System.out.printf(" ");dateFormatPut(date1); 270 } 271 } 272 //数据格式输出 273 public static void dateFormatPut(double date) { 274 if(Math.abs(date-(int)date)<10e-6||Math.abs(date-(int)date+1)<10e-6||Math.abs(date-(int)date-1)<10e-6) { 275 System.out.printf("%.1f",date); 276 }else { 277 String d = String.valueOf(date); 278 if(d.length()-1-d.indexOf('.')>3){ 279 System.out.printf("%.3f",date); 280 }else { 281 System.out.print(date); 282 } 283 } 284 } 285 //求直线切三角形交点个数和分割面积 286 public static void intersectionNumber_dividedArea(line L, point p1,point p2,point p3) { 287 line l12 = new line(p1, p2);line l23 = new line(p2, p3);line l13 = new line(p1, p3); 288 if(L.threePoint_Same_place(p1, p2, p3)) {//无交点 289 System.out.println(0); 290 }else if( ( L.point_on_line(p1)&&L.twoPoint_Same_place(p2, p3) )||( L.point_on_line(p2)&&L.twoPoint_Same_place(p1, p3) ) ||( L.point_on_line(p3)&&L.twoPoint_Same_place(p1, p2) ) ) {//一个交点 291 System.out.println(1); 292 }else if(L.firstPoint_laterTwoPoints_different_place(p1, p2, p3) ) { 293 dateCompare_FormatPut( triangleArea(p1, L.twoLineIntersection(l12), L.twoLineIntersection(l13) ), triangleArea(p1, p2, p3)-triangleArea(p1, L.twoLineIntersection(l12), L.twoLineIntersection(l13) ) ); 294 }else if(L.firstPoint_laterTwoPoints_different_place(p2, p1, p3)) { 295 dateCompare_FormatPut( triangleArea(p2, L.twoLineIntersection(l12), L.twoLineIntersection(l23) ), triangleArea(p1, p2, p3)-triangleArea(p2, L.twoLineIntersection(l12), L.twoLineIntersection(l23) ) ); 296 }else if(L.firstPoint_laterTwoPoints_different_place(p3, p1, p2)) { 297 dateCompare_FormatPut( triangleArea(p3, L.twoLineIntersection(l13), L.twoLineIntersection(l23) ), triangleArea(p1, p2, p3)-triangleArea(p3, L.twoLineIntersection(l13), L.twoLineIntersection(l23) ) ); 298 } 299 } 300 //判断输入格式是否合法 301 public static boolean isFormatTure(String date) { 302 String regex = "[1-5]:((\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*),(\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*) )*((\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*),(\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*)( )?)+"; 303 boolean isFormatTure = date.matches(regex); 304 return isFormatTure; 305 } 306 //提取坐标数据并将String型坐标转为double型坐标 307 public static double[] splitDate_transform(String date) { 308 Pattern pattern = Pattern.compile("(-?\\d*)\\.?\\d+"); //创建个匹配器对刻 309 Matcher matcher1 = pattern.matcher(date); 310 int count = 0,i = 0; 311 while (matcher1.find()){ 312 count++; 313 } 314 double[] array = new double[count-1]; 315 Matcher matcher2 = pattern.matcher(date); 316 while (matcher2.find()){ 317 if(i>0) { 318 array[i-1] = Double.parseDouble(matcher2.group(0)); 319 } 320 i++; 321 } 322 return array; 323 } 324 } 325 326 class point{ 327 private double x; 328 private double y; 329 330 public point(double x, double y) { 331 super(); 332 this.x = x; 333 this.y = y; 334 } 335 public double getX() { 336 return x; 337 } 338 public double getY() { 339 return y; 340 } 341 //两点重合 342 public boolean pointsCoincide(point p) { 343 return x==p.getX()&&y==p.getY(); 344 } 345 //两点距离 346 public double twoPointslength(point p) { 347 return Math.sqrt( Math.pow(x-p.getX(),2) + Math.pow(y-p.getY(),2) ); 348 } 349 } 350 class line{ 351 private point p1; 352 private point p2; 353 354 public line(point p1, point p2) { 355 super(); 356 this.p1 = p1; 357 this.p2 = p2; 358 } 359 public point getP1() { 360 return p1; 361 } 362 public point getP2() { 363 return p2; 364 } 365 //一个点在一条线上 366 public boolean point_on_line(point p) { 367 return (p1.getY()-p2.getY())*p.getX()-(p1.getX()-p2.getX())*p.getY()+p1.getX()*p2.getY()-p2.getX()*p1.getY()==0; 368 } 369 //一个点在一条线段上(含端点) 370 public boolean pointOnLineSegment(point p) { 371 return point_on_line(p)&&( (p.getX()-p1.getX())*(p.getX()-p2.getX())<=0&&(p.getY()-p1.getY())*(p.getY()-p2.getY())<=0 ); 372 } 373 //判断斜率 374 public String judgeSlope() { 375 if(p1.getX()!=p2.getX()) { 376 if((p1.getY()-p2.getY())/(p1.getX()-p2.getX())==0) { 377 return ""+0.0; 378 } 379 return ""+(p1.getY()-p2.getY())/(p1.getX()-p2.getX()); 380 }else { 381 return "false"; 382 } 383 } 384 //判断两直线是否重合 385 public boolean twoLinesCoincide(line l) { 386 return l.point_on_line(p1)&&l.point_on_line(p2); 387 } 388 //求两直线正弦 389 public double twoLineAngleSine(line l) { 390 return Math.sqrt(1-Math.pow(Math.abs( (p1.getX()-p2.getX())*(l.getP1().getX()-l.getP2().getX())+(p1.getY()-p2.getY())*(l.getP1().getY()-l.getP2().getY()) )/(p1.twoPointslength(p2)*l.getP1().twoPointslength(l.getP2())), 2)); 391 } 392 //两直线交点 393 public point twoLineIntersection(line l) { 394 double x1=p1.getX(),x2=p2.getX(),y1=p1.getY(),y2=p2.getY(),x3=l.getP1().getX(),x4=l.getP2().getX(),y3=l.getP1().getY(),y4=l.getP2().getY(); 395 if(judgeSlope()==l.judgeSlope()) { 396 return null; 397 } 398 double yy=((x4*y3-y4*x3)*(y1-y2)-(x2*y1-y2*x1)*(y3-y4))/((x1-x2)*(y3-y4)-(x3-x4)*(y1-y2)); 399 double xx = 0; 400 if(y1!=y2) { 401 xx=((x1-x2)*(yy-y1)+(y1-y2)*x1)/(y1-y2); 402 }else { 403 xx=((x3-x4)*(yy-y3)+(y3-y4)*x3)/(y3-y4); 404 } 405 point p = new point(xx,yy); 406 return p; 407 } 408 //以一条线为边界,判断一点的位置。 409 public int onePoint_place(point p) { 410 double x1=p1.getX(),x2=p2.getX(),y1=p1.getY(),y2=p2.getY(),x3=p.getX(),y3=p.getY(); 411 // if(judgeSlope().equals("false")) {//斜率不存在时,在直线右边返回1,线上返回0,左边返回-1; 412 // if(x3>x1) { 413 // return 1; 414 // }else if(x3==x1) { 415 // return 0; 416 // }else {//(x3-x1<0) 417 // return -1; 418 // } 419 // }else {//斜率存在时,在直线上边返回1,线上返回0,下边返回-1; 420 if(y3>(y2-y1)/(x2-x1)*(x3-x1)+y1) { 421 return 1; 422 }else if(y3==(y2-y1)/(x2-x1)*(x3-x1)+y1) { 423 return 0; 424 }else {//(y3<(y2-y1)/(x2-x1)*(x3-x1)+y1) 425 return -1; 426 } 427 // } 428 } 429 430 //以一条线为边界,判断四点同侧 431 public boolean fourPoint_Same_place(point pp1, point pp2, point pp3, point pp4) { 432 return ( ( onePoint_place(pp1)>0&&onePoint_place(pp2)>0&&onePoint_place(pp3)>0&&onePoint_place(pp4)>0 )||( onePoint_place(pp1)<0&&onePoint_place(pp2)<0&&onePoint_place(pp3)<0&&onePoint_place(pp4)<0 ) ); 433 } 434 //以一条线为边界,判断三点同侧 435 public boolean threePoint_Same_place(point pp1, point pp2, point pp3) { 436 return ( ( onePoint_place(pp1)>0&&onePoint_place(pp2)>0&&onePoint_place(pp3)>0 )||( onePoint_place(pp1)<0&&onePoint_place(pp2)<0&&onePoint_place(pp3)<0 ) ); 437 } 438 //以一条线为边界,两点是否异侧 439 public boolean twoPoint_Same_place(point pp1,point pp2) { 440 return ( ( onePoint_place(pp1)>0&&onePoint_place(pp2)>0 )||( onePoint_place(pp1)<0&&onePoint_place(pp2)<0 ) ); 441 } 442 //以一条线为边界,判断第一点与其他三点异侧 443 public boolean firstPoint_laterThreePoints_different_place(point pp1, point pp2, point pp3, point pp4) { 444 return ( ( onePoint_place(pp1)<0&&onePoint_place(pp2)>0&&onePoint_place(pp3)>0&&onePoint_place(pp4)>0 )||( onePoint_place(pp1)>0&&onePoint_place(pp2)<0&&onePoint_place(pp3)<0&&onePoint_place(pp4)<0 ) ); 445 } 446 //以一条线为边界,判断前两个点与其他后两点异侧 447 public boolean firstTwoPoints_laterTwoPoints_different_place(point pp1, point pp2, point pp3, point pp4) { 448 return ( ( onePoint_place(pp1)<0&&onePoint_place(pp2)<0&&onePoint_place(pp3)>0&&onePoint_place(pp4)>0 )||( onePoint_place(pp1)>0&&onePoint_place(pp2)>0&&onePoint_place(pp3)<0&&onePoint_place(pp4)<0 ) ); 449 } 450 //以一条线为边界,判断第一点与其他两点异侧 451 public boolean firstPoint_laterTwoPoints_different_place(point pp1, point pp2, point pp3) { 452 return ( ( onePoint_place(pp1)<0&&onePoint_place(pp2)>0&&onePoint_place(pp3)>0 )||( onePoint_place(pp1)>0&&onePoint_place(pp2)<0&&onePoint_place(pp3)<0 ) ); 453 } 454 //以一条线为边界,两点是否异侧 455 public boolean twoPointDifferentSide(point pp1,point pp2) { 456 return ( ( onePoint_place(pp1)<0&&onePoint_place(pp2)>0 )||( onePoint_place(pp1)>0&&onePoint_place(pp2)<0 ) ); 457 } 458 //点到直线的距离 459 public double pointLineDistance(point p) { 460 return Math.abs((p2.getY()-p1.getY())*p.getX()+(p1.getX()-p2.getX())*p.getY()+p2.getX()*p1.getY()-p1.getX()*p2.getY())/Math.sqrt((p2.getY()-p1.getY())*(p2.getY()-p1.getY())+(p1.getX()-p2.getX())*(p1.getX()-p2.getX())); 461 } 462 463 }
4.踩坑心得
①判断是否为凸四边形还要考虑输入的相邻坐标是否是四边形的相邻顶点
方法:设输入的四个坐标依次为A、B、C、D
以对角线AC为例,B、D两点一定在AC的异侧
②double型数据计算可能会出现精度问题,明明结果为6.0,却输出5.9999999975或6.0000000075(顺便举的例子),下图即输出正确格式(本题还要求超过3位小数保留3位,小于等于3位小数输出本身)的方法·
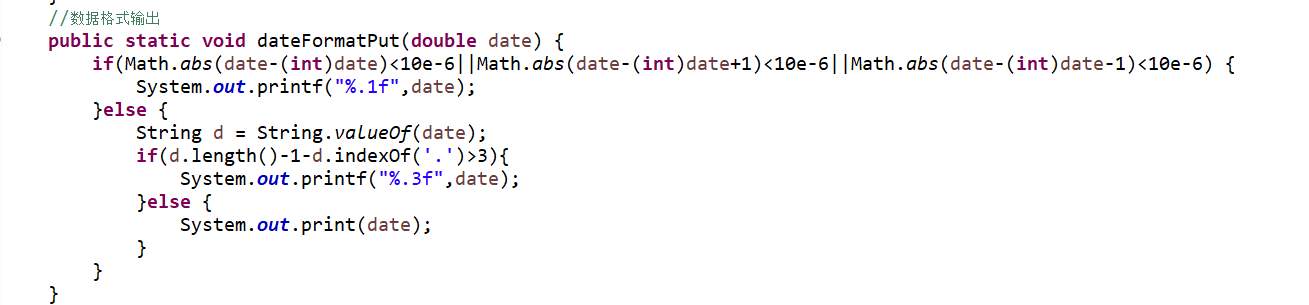
5.改进建议
本题并未考察凹四边形,凹四边形输入坐标的顺序是否正确太难,还没有想出来
三、链表
1.源码设计解释:
接口:

节点类:

节点类包括数据域和指针域
链表类:
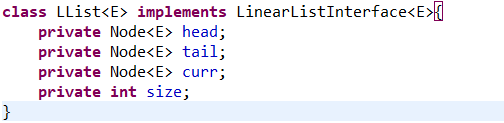
其中head为头指针,tail为尾指针
2.源码:(很长,已折叠,记得点加号打开)

1 package Linkedlist; 2 3 interface LinearListInterface<E> {//泛型接口 4 public boolean isEmpty(); 5 public int size(); 6 public E get(int index); 7 public void remove(int index); 8 public void add(int index, E theElement); 9 public void add(E element); 10 public void printList(); 11 } 12 //LinkedList class 13 class LList<E> implements LinearListInterface<E>{ 14 private Node<E> head; 15 private Node<E> tail; 16 private Node<E> curr; 17 private int size; 18 @Override 19 public boolean isEmpty() {//判断当前节点是否为空节点 20 // TODO Auto-generated method stub 21 if(this.curr==null) { 22 return true; 23 } 24 return false; 25 } 26 @Override 27 public int size() { 28 // TODO Auto-generated method stub 29 return this.size; 30 } 31 @Override 32 public E get(int index) {//获得第Index节点的值 33 // TODO Auto-generated method stub 34 int count = 0; 35 if(index>=0&&index<=size) { 36 this.curr = head; 37 while(count<index) { 38 this.curr = this.curr.next; 39 count++; 40 } 41 return this.curr.o;//返回当前节点 42 } 43 return null; 44 } 45 @Override 46 public void remove(int index) { 47 // TODO Auto-generated method stub 48 int count = 0; 49 if(index>=0&&index<=size) { 50 if(index==0) {//删除头部 51 this.head = this.head.next; 52 this.size--; 53 }else { 54 this.curr = this.head; 55 while(count<index-1) { 56 this.curr = this.curr.next; 57 count++; 58 } 59 this.curr.next = this.curr.next.next; 60 } 61 this.size--; 62 } 63 64 } 65 @Override 66 public void add(int index, E theElement) {//任意位置添加节点 67 // TODO Auto-generated method stub 68 int count = 0; 69 if(index>=0&&index<=this.size) { 70 if(index==0) { 71 this.head = new Node<E>(theElement,this.head);//如果添加在头部,theElement成为新头部 72 }else { 73 this.curr = head; 74 while(count<index-1) {//找到要添加节点的位置 75 this.curr = this.curr.next; 76 count++; 77 } 78 this.curr.next = new Node<E>(theElement,this.curr.next); 79 } 80 this.size++; 81 } 82 83 } 84 @Override 85 public void add(E element) {//尾部添加节点 86 // TODO Auto-generated method stub 87 Node<E> node =new Node<E>(element,null);//新节点 88 this.curr = this.tail;// 89 this.tail = node; 90 if(isEmpty()) { 91 head = node; 92 }else{ 93 curr.next = node; 94 } 95 this.size++; 96 } 97 @Override 98 public void printList() { 99 // TODO Auto-generated method stub 100 for(int i = 0;i<this.size;i++) { 101 System.out.print(get(i).toString()+" "); 102 } 103 } 104 105 } 106 //Node 107 108 class Node<E>{//节点 109 public E o;//数据域 110 public Node<E> next;//指针域 111 112 public Node(E o,Node<E> next) {//构造器 113 this.o = o; 114 this.next = next; 115 } 116 } 117 118 119 public class Lianbiao { 120 121 public static void main(String[] args) { 122 // TODO Auto-generated method stub 123 LList<Integer> list = new LList<Integer>(); 124 for(int i = 0;i<10;i++) { 125 list.add(i); 126 } 127 list.printList();//输出链表 128 list.remove(12);//删除第四个节点 129 System.out.println("\n删除第四个节点后的链表:"); 130 list.printList();//输出链表 131 list.add(4, 4);//第四个节点添加4 132 System.out.println("\n增加第四个节点后的链表:"); 133 list.printList();//输出链表 134 } 135 }
3.踩坑心得:
链表的结构很简单,就是一个个节点连接在一起,形成一个完整的链条,每个节点包含2部分,数据域,和一个指向下一个节点引用的指针next,具体的更详细的大家可以参考相关资料解释,再说说删除操作,同样需要找到数据所在的位置,然后进行删除,不同的是,删除的时候,链表只需要改变一下前后节点的引用关系即可,就完成了节点的删除,而没有像数组那样触发一次全部数据的移动,从这个描述来看,链表在进行删除的时候,速度比数组快。
4.改进建议:
不能够自定义实现链表,应当做适当修改。
四、期中考试分析
1.点与线(类设计)

①源码设计解释:
②源码:(很长,已折叠,记得点加号打开)

1 import java.util.Scanner; 2 3 public class Main { 4 5 public static void main(String[] args) { 6 Scanner in = new Scanner(System.in); 7 double x1=in.nextDouble(),y1=in.nextDouble(),x2=in.nextDouble(),y2=in.nextDouble(); 8 String color = new String(in.next()); 9 if( (x1<=0||x1>200) ||(y1<=0||y1>200)||(x2<=0||x2>200) ||(y2<=0||y2>200) ) { 10 System.out.println("Wrong Format"); 11 System.exit(0); 12 } 13 Point point1 = new Point(x1,y1); 14 Point point2 = new Point(x2,y2); 15 Line line = new Line(point1,point2,color) ; 16 line.display(); 17 } 18 } 19 20 class Point { 21 private double x; 22 private double y; 23 public Point() { 24 25 } 26 public Point(double x, double y) { 27 super(); 28 29 this.x = x; 30 this.y = y; 31 } 32 public double getX() { 33 return x; 34 } 35 public void setX(double x) { 36 this.x = x; 37 } 38 public double getY() { 39 return y; 40 } 41 public void setY(double y) { 42 this.y = y; 43 } 44 45 public void display() { 46 System.out.print("("); 47 System.out.printf("%.2f",this.x); 48 System.out.print(","); 49 System.out.printf("%.2f",this.y); 50 System.out.println(")"); 51 } 52 public static boolean pointPutIsFormatTure(double date) { 53 return date>0&&date<=200; 54 } 55 } 56 57 class Line { 58 private Point point1; 59 private Point point2; 60 private String color; 61 public Line() { 62 super(); 63 } 64 public Line(Point point1, Point point2, String color) { 65 super(); 66 this.point1 = point1; 67 this.point2 = point2; 68 this.color = color; 69 } 70 71 public Point getPoint1() { 72 return point1; 73 } 74 public void setPoint1(Point point1) { 75 this.point1 = point1; 76 } 77 public Point getPoint2() { 78 return point2; 79 } 80 public void setPoint2(Point point2) { 81 this.point2 = point2; 82 } 83 public String getColor() { 84 return color; 85 } 86 public void setColor(String color) { 87 this.color = color; 88 } 89 public double getDistance() { 90 return Math.sqrt(Math.pow(this.point1.getX()-this.point2.getX(),2) + Math.pow(this.point1.getY()-this.point2.getY(),2)); 91 } 92 public void display() { 93 System.out.println("The line's color is:"+this.color); 94 System.out.println("The line's begin point's Coordinate is:"); 95 this.point1.display(); 96 System.out.println("The line's end point's Coordinate is:"); 97 this.point2.display(); 98 System.out.print("The line's length is:"); 99 System.out.printf("%.2f",getDistance()); 100 101 } 102 103 } 104 105 106 107
③说明:
最基础的类的设计,通过创建对象然后调用类中的方法实现对点和线信息的输出
2、7-2 点线面问题重构(继承与多态)
下面对点线面问题重构,新增一个抽象类Element,点类和线类成为该类的子类,再创建一个面类,也是Element的子类
①源码:

1 import java.util.Scanner; 2 3 public class Main { 4 5 public static void main(String[] args) { 6 Scanner in = new Scanner(System.in); 7 double x1=in.nextDouble(),y1=in.nextDouble(),x2=in.nextDouble(),y2=in.nextDouble(); 8 String color = new String(in.next()); 9 if( (x1<=0||x1>200) ||(y1<=0||y1>200)||(x2<=0||x2>200) ||(y2<=0||y2>200) ) { 10 System.out.println("Wrong Format"); 11 System.exit(0); 12 } 13 Point p1 = new Point(x1,y1); 14 Point p2 = new Point(x2,y2); 15 Line line = new Line(p1,p2,color) ; 16 // line.display(); 17 Plane plane = new Plane(color) ; 18 Element element1 = p1;//起点Point 19 element1.display(); 20 21 Element element2 = p2;//终点Point 22 element2.display(); 23 24 Element element3 = line;//线段 25 element3.display(); 26 27 Element element4 = plane;//面 28 element4.display(); 29 30 } 31 } 32 33 class Point extends Element{ 34 private double x; 35 private double y; 36 public Point() { 37 38 } 39 public Point(double x, double y) { 40 super(); 41 42 this.x = x; 43 this.y = y; 44 } 45 public double getX() { 46 return x; 47 } 48 public void setX(double x) { 49 this.x = x; 50 } 51 public double getY() { 52 return y; 53 } 54 public void setY(double y) { 55 this.y = y; 56 } 57 58 public void display() { 59 System.out.print("("); 60 System.out.printf("%.2f",this.x); 61 System.out.print(","); 62 System.out.printf("%.2f",this.y); 63 System.out.println(")"); 64 } 65 public static boolean pointPutIsFormatTure(double date) { 66 return date>0&&date<=200; 67 } 68 } 69 70 class Line extends Element { 71 private Point point1; 72 private Point point2; 73 private String color; 74 public Line() { 75 super(); 76 } 77 public Line(Point point1, Point point2, String color) { 78 super(); 79 this.point1 = point1; 80 this.point2 = point2; 81 this.color = color; 82 } 83 84 public Point getPoint1() { 85 return point1; 86 } 87 public void setPoint1(Point point1) { 88 this.point1 = point1; 89 } 90 public Point getPoint2() { 91 return point2; 92 } 93 public void setPoint2(Point point2) { 94 this.point2 = point2; 95 } 96 public String getColor() { 97 return color; 98 } 99 public void setColor(String color) { 100 this.color = color; 101 } 102 public double getDistance() { 103 return Math.sqrt(Math.pow(this.point1.getX()-this.point2.getX(),2) + Math.pow(this.point1.getY()-this.point2.getY(),2)); 104 } 105 public void display() { 106 System.out.println("The line's color is:"+this.color); 107 System.out.println("The line's begin point's Coordinate is:"); 108 this.point1.display(); 109 System.out.println("The line's end point's Coordinate is:"); 110 this.point2.display(); 111 System.out.print("The line's length is:"); 112 System.out.printf("%.2f",getDistance()); 113 System.out.println(); 114 } 115 116 } 117 118 class Element{ 119 120 121 public void display() { 122 123 } 124 } 125 class Plane extends Element{ 126 private String color; 127 128 public Plane(String color) { 129 super(); 130 this.color = color; 131 } 132 133 public String getColor() { 134 return color; 135 } 136 137 public void setColor(String color) { 138 this.color = color; 139 } 140 141 public void display() { 142 System.out.print("The Plane's color is:"); 143 System.out.printf(color); 144 } 145 } 146 147
②说明:
在主方法内,定义两个Point对象、一个Line对象和一个Plane对象,依次从键盘输入两个Point对象的起点、终点坐标和颜色值(Line对象和Plane对象颜色相同),然后定义一个Element类的引用,分别使用该引用调用以上四个对象的display()方法,这就实现了多态特性。
3、7-3 点线面问题再重构(容器类)
下面在“点与线”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
①源码:

1 import java.util.ArrayList; 2 import java.util.Scanner; 3 4 public class Main { 5 6 public static void main(String[] args) { 7 // TODO Auto-generated method stub 8 GeometryObject geo = new GeometryObject(); 9 Scanner in = new Scanner(System.in); 10 while(true) { 11 int choice = in.nextInt(); 12 if(choice==0) { 13 break; 14 } 15 switch(choice) { 16 case 1: 17 double px = in.nextDouble(); 18 double py = in.nextDouble(); 19 if(px<=0||px>200||py<=0||py>200) { 20 System.out.println("Wrong Format"); 21 System.exit(0); 22 } 23 geo.add(new Point(px,py)); 24 break; 25 case 2: 26 double ppx = in.nextDouble(); 27 double ppy = in.nextDouble(); 28 double qx = in.nextDouble(); 29 double qy = in.nextDouble(); 30 String color = in.next(); 31 if(ppx<=0||ppx>200||ppy<=0||ppy>200||qx<=0||qx>200||qy<=0||qy>200) { 32 System.out.println("Wrong Format"); 33 System.exit(0); 34 } 35 Point p = new Point(ppx,ppy); 36 Point q = new Point(qx,qy); 37 Line l = new Line(p,q,color); 38 geo.add(l); 39 break; 40 case 3: 41 String planecolor = in.next(); 42 Plane plane = new Plane(planecolor); 43 geo.add(plane); 44 break; 45 case 4: 46 int choose = in.nextInt(); 47 geo.remove(choose); 48 break; 49 default: 50 break; 51 } 52 } 53 for(Element element : geo.getList()) { 54 element.display(); 55 } 56 } 57 58 } 59 60 class Point extends Element{ 61 private double x = 0; 62 private double y = 0; 63 64 public Point(double x,double y) { 65 this.x = x; 66 this.y = y; 67 } 68 @Override 69 public void display() { 70 System.out.printf("(%.2f,%.2f)\n",this.x,this.y); 71 } 72 73 public double getX() { 74 return this.x; 75 } 76 77 public double getY() { 78 return this.y; 79 } 80 81 public void setX(double x) { 82 this.x = x; 83 } 84 85 public void setY(double y) { 86 this.y = y; 87 } 88 } 89 90 class Line extends Element{ 91 private Point point1; 92 private Point point2; 93 private String color; 94 95 public Line(Point p1,Point p2,String color) { 96 this.point1 = p1; 97 this.point2 = p2; 98 this.color = color; 99 } 100 101 public Point getPoint1() { 102 return point1; 103 } 104 105 public Point getPoint2() { 106 return point2; 107 } 108 109 public void setPoint1(Point point1) { 110 this.point1 = point1; 111 } 112 113 public void setPoint2(Point point2) { 114 this.point2 = point2; 115 } 116 117 public String getColor() { 118 return color; 119 } 120 121 public void setColor(String color) { 122 this.color = color; 123 } 124 125 public double getDistance() { 126 return Math.sqrt(Math.pow(this.point1.getX()-this.point2.getX(), 2)+Math.pow(this.point1.getY()-this.point2.getY(), 2)); 127 } 128 @Override 129 public void display() { 130 System.out.println("The line's color is:"+this.getColor()); 131 System.out.println("The line's begin point's Coordinate is:"); 132 System.out.printf("(%.2f,%.2f)\n",this.point1.getX(),this.point1.getY()); 133 System.out.println("The line's end point's Coordinate is:"); 134 System.out.printf("(%.2f,%.2f)\n",this.point2.getX(),this.point2.getY()); 135 System.out.printf("The line's length is:%.2f",this.getDistance()); 136 System.out.printf("\n"); 137 } 138 } 139 140 abstract class Element{ 141 public void display() { 142 143 } 144 } 145 146 class Plane extends Element{ 147 private String color; 148 149 public Plane(String color) { 150 this.color = color; 151 } 152 153 public String getColor() { 154 return color; 155 } 156 157 public void setColor() { 158 this.color = color; 159 } 160 161 public void display() { 162 System.out.println("The Plane's color is:"+this.getColor()); 163 } 164 } 165 166 class GeometryObject{ 167 private ArrayList<Element> list = new ArrayList<>(); 168 169 public void add(Element element) { 170 list.add(element); 171 } 172 173 public void remove(int index) { 174 if(index<=list.size()) { 175 list.remove(index-1); 176 } 177 } 178 179 public ArrayList<Element> getList(){ 180 return list; 181 } 182 }
②说明:
ArrayList相当于一个对象容器,里面存入的是Element类型的,这就能够完成增、删、遍历操作。
4、采坑心得:
(1)给有相同性质的类设计一个父类是一个很好的编程思维,再进行相关操作的时候使用向上造型实现多态特性,这不仅能提高代码的复用性还能使代码更加的简洁,编程效率更加高效
(2)使用泛型也是一种很好的编程思维,能够实现增、删、遍历操作。对任意的一个对象都能够修改。
总结:
学会了什么:
1.通过对本阶段综合性总结,我对Java的基础语法(选择、函数、字符字符串相关操作、循环、方法、数组)有了更深层次的理解
2.对类与对象的设计原则有了更深层次的理解,了解了继承原则和多态特性,并能在实际编程加以应用
3.了解了什么是接口、并能熟练应用
还需要改进加强的地方:
1.考虑问题不够全面
2.主函数不能做到完全解耦
3.算法不够精确不够简单





 浙公网安备 33010602011771号
浙公网安备 33010602011771号