圆方树

前置知识：点双连通分量

定义

圆方树：对于一个点双内的点，拆除点之间所有相连的边，并和一个代表该点双的点连边

圆点为原图中的点，方点代表一个点双

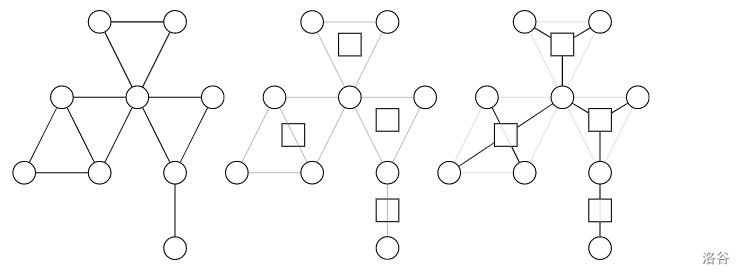
圆方树有狭义和广义两种

狭义圆方树不把“杠铃形”当作点双，有圆圆边

广义圆方树把“杠铃形”当作点双，只有圆方边

狭义圆方树是解决仙人掌问题的利器，详见link

广义圆方树一般图都能用

建树

（模板题我在这卡了2h……）

对于仙人掌图，可以魔改tarjan，当搜到dfn[v]<dfn[x]的点时，说明一定成环，在此处直接跑环更方便（详见代码）

对于一般图，上标准的tarjan即可

代码

仙人掌图：

void tarjan(int x,int pre) {
	dfn[x]=low[x]=++index;
	st[++stpos]=x;
	erg(G,x,i) {
		int v=G.e[i].to;
		if(i==(pre^1)) continue;
		if(!dfn[v]) {
			dis[v]=dis[x]+G.e[i].dis;
			tarjan(v,i);
			low[x]=min(low[x],low[v]);
			if(low[v]>=dfn[x]) {
				if(low[v]>dfn[x]) {
					T.Addedge(x,v,G.e[i].dis);
					T.Addedge(v,x,G.e[i].dis);
				}
				while(st[stpos]!=x) stpos--;	//正常图在这里统计点双 
			}
		}
		else {
			low[x]=min(low[x],dfn[v]);
			if(low[x]!=dfn[v]) continue;
			sum[++ntot]=dis[x]-dis[v]+G.e[i].dis;	//仙人掌因为要用环的边权和sum[]，在此处求更方便 
			for(int j=stpos;st[j+1]!=v;j--) {
				T.Addedge(ntot,st[j],min(dis[st[j]]-dis[v],sum[ntot]-(dis[st[j]]-dis[v])));
				T.Addedge(st[j],ntot,min(dis[st[j]]-dis[v],sum[ntot]-(dis[st[j]]-dis[v])));
			}	
		}
	}
}

细节