生成树

Prim

Kruscal

Kruscal重构树

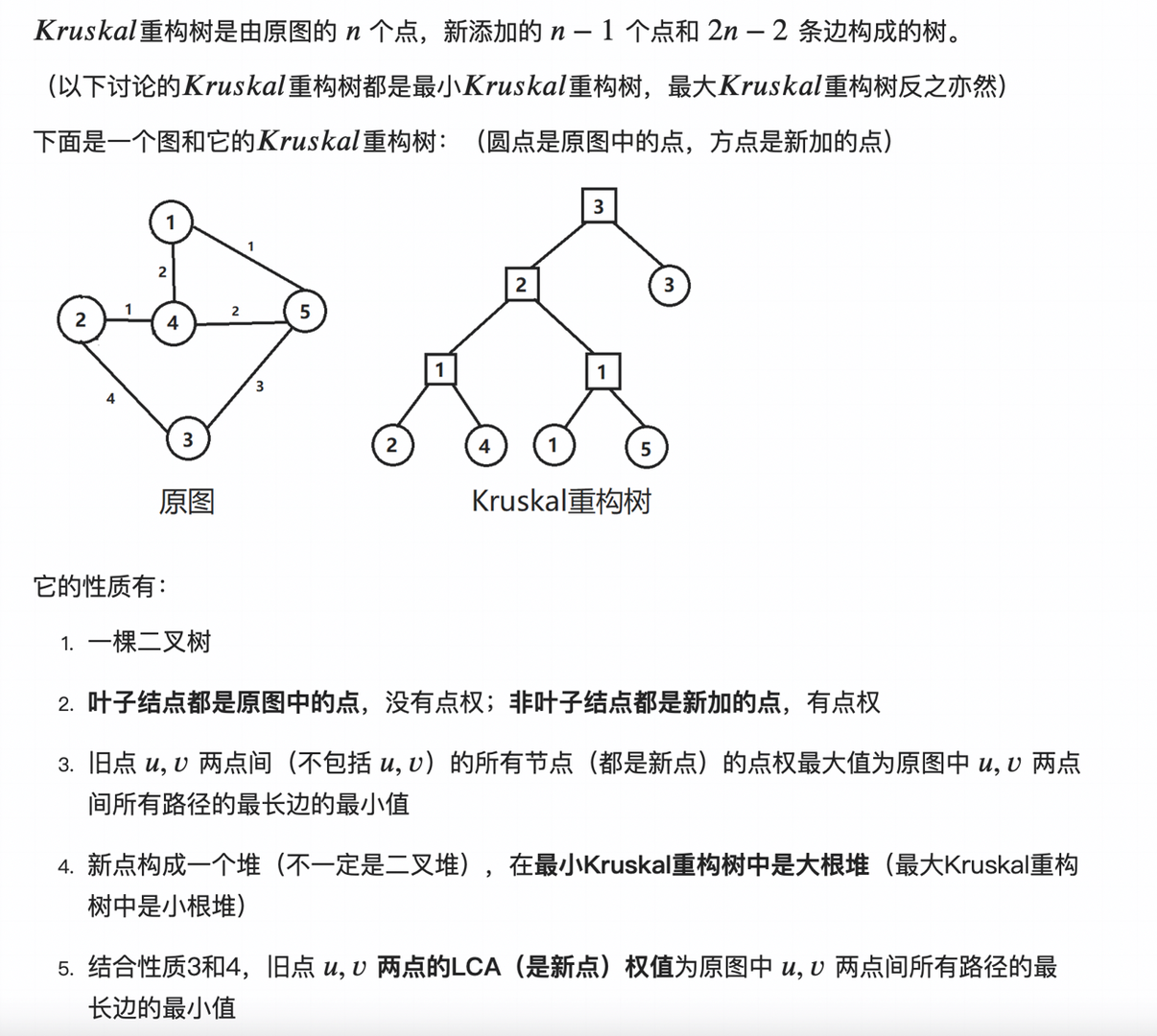
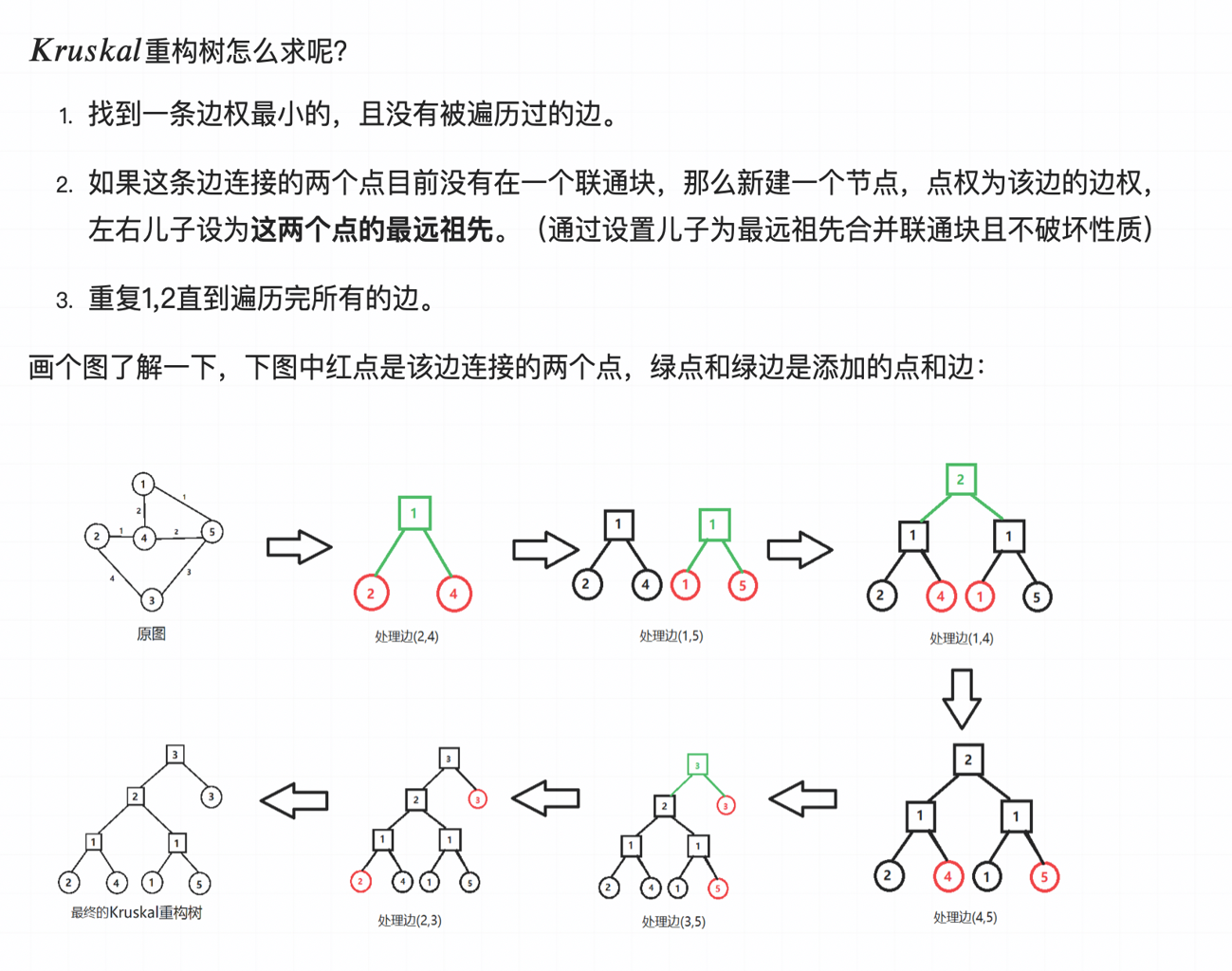
由于Kruscal重构树是二叉堆，且瓶颈路最大值在LCA上，可以进行一些树上操作（主席树、树上倍增等）

（看看这篇）

P4768 [NOI2018] 归程

要求\(v\)所在海拔高于\(p\)的连通块到结点\(1\)的最短路，易知尽量走海拔高的边连通块会拓展至更多点，则一个点是否能到达另一个点只受海拔尽量大的路径中海拔最小的边的限制，符合瓶颈路的定义，做Kruscal重构树+树上倍增可以快速取到能到达的所有点的dis值

p.s. Build()的赋值把0的父亲给赋了，本地跑又没问题，调了一个钟

P6765 [APIO2020] 交换城市

分析得，连通块非链即合法，权值为使该路径非链的边最小权

魔改Kruscal重构树：由于链不合法，成为非链时才有权，把此时链上全部点向新点连边，新点点权为当前加边\(w[i]\)（因为链上两两互达必须经过该边）

维护链可以用并查集+启发式合并

p.s. 我的思路：只有路径带环和非路端有三岔路合法，用倍增维护相关路径的最小、次小等值即可（但是会非常难写，果然瓶颈路还得是Kruscal重构树

瓶颈路

最小瓶颈路：\(u \to v\) 全部路径中权值最大的边最小的路径

重要性质：最小瓶颈路一定在最小生成树上

浅证：设最小生成树的最大边权为\(maxd\)，假设存在一条路径的权值最大的边不在最小生成树上且小于\(maxd\)，则在Kruscal建树时应已经加入，故不存在

由该性质可解决一些瓶颈路问题

例1：P1967 [NOIP2013 提高组] 货车运输

瓶颈路经典问题

例2：P1902 刺杀大使

求最大点权最小，类似瓶颈路，考虑生成树相关算法

可以在Kruscal上稍做修改，每次贪心加边，到起点、终点联通时停止

次小生成树