算法及其复杂度的学习总结

本人刚开始学习算法，想讲每天学习的笔记分享给大家，有什么不对的地方，希望大家都能提出来。

一．什么是算法

   1.1算法是用于解决待定问题的一系列的执行步骤。

   例如：计算a和b的和：

public static int plus(int a,int b) {
        return a+b;
}

 

这就是一个算法。

 

   1.2使用不同的算法，解决同一个问题，效率会相差很大。

   例如：求第n个斐波那契数。

/*1,1,2,3,5,8......这种从第三个数开始为前两个数的和的数叫做契波那契数*/

   方法一：递归法

    public static int fib1(int n) {
        if(n==1||n==2) return 1;
        else return fib1(n-1)+fib1(n-2);
        
    }

方法二：for循环

 

 public static int fib2(int n) {
        if(n==1||n==2) return 1;
        int first = 1;//定义初始值
        int second =1;//定义初始值
        int sum=0;//定义总和
        for(int i =0;i<n-2;i++) {
            sum = first+second;
            first = second;
            second = sum;//将数字向前推进
        }
        return second;
    }

 

我们看这两种算法，在我们求第64个数字时

方法二能够快速的算出，然而方法一却不能算出。因此，方法一和方法二的效率相差很大。

 

 

补充：递归法的时间复杂度：O（2^n）

      for循环的时间复杂度：O(n)

 

二、算法的评估

方法一：事后统计法

事后统计法就是比较不同算法对同一组输入的执行处理时间。我们刚刚使用的方法就是事后统计法。

这种方法有着以下的缺点：

1. 执行时间严重依赖硬件以及运行时各种不确定的环境。
2. 必须编写相应的测试代码
3. 测试数据的选择比较难保证公平性。

因此我们常常不用这种方法。

 

 

方法二：通过时间和空间复杂度来评估算法的优劣

时间复杂度:估算程序指令的执行次数（执行时间）

空间复杂度:估算所需占用的存储空间。

 

 

 

三、时间复杂度和大O表示法

大O表示法表示数据规模n对应的复杂度。忽略常数、系数、低价。

大O表示法仅仅是一种粗略的分析模型，是一种估算，能帮助我们短时间了解一个算法的执行效率。

常见的时间复杂度：

 

 

 

 

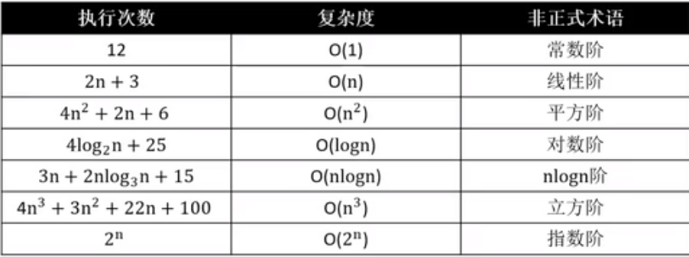
例一：下面的代码只执行了一次，所以时间复杂度是O(1)  

public static void test1(int n) {
        if(n>10) {
        System.out.println("n>10");}
        else if(n>5) {
            System.out.println("n>5");
        }
        else {
            System.out.println("test");
        }
    }

例二：下面的代码：int i=0执行了1次。i<n,i++,System.out.println("test")在每一次循环之后又会再一次执行，所以执行的次数是：3n。所以总的执行次数是3n+1，时间复杂度是O(n)。       

 

public static void test2(int n) {
        for(int i=0;i<n;i++) {
            System.out.println("test");
        }
    }

 

例三：外部for循环：int i=0表示执行了一次，为1。 i<n,i++在每一次循环之后又会再一次执行，所以执行的次数是：2n。

内部for循环：int j=0表示执行了1次，j<n,j++,System.out.println("test")在每一次循环之后又会再一次执行，所以执行的次数是：3n.由因为外部for循环则执行总次数为：n*(1+3n)

整个程序的执行次数为1+2n+n*(1+3n)=3n^2+3n+1,时间复杂度是O(n^2) 

public static void test3(int n) {
        for(int i=0;i<n;i++) {
        for(int j=0;j<n;j++) {
            System.out.println("test");
        }
        }
        }

例四：由例三可知，执行次数是48n+1,时间复杂度是O(n)

public static void test4(int n) {
        
        for(int i=0;i<n;i++) {
            for(int j=0;j<15;j++) {
                System.out.println("test");
            }
            }
        
    }

例五：while((n=n/2)>0)表示n能除以多少个2，就能执行几次。

假设n能除以多少个2为m

      那么2^m=n

m=log2(n)

整个程序的执行次数为：log2(n),时间复杂度是O(logn)

 public static void test5(int n) {
        while((n=n/2)>0) {
            System.out.println("test");
        }
}

例六：外部for循环：int i=1表示执行了一次，为1。 i<n,i=i*2在每一次循环之后又会再一次执行，i=i*2与例五相同，所以执行的次数是：2*log2(n)。

内部for循环：int j=0表示执行了1次，j<n,j++,System.out.println("test")在每一次循环之后又会再一次执行，所以执行的次数是：3n.由因为外部for循环则执行总次数为：n*(1+3n)

整个程序的执行次1+2*log2(n)+log2(n)*(1+3n)=1+3*log2(n)+2*log2(n),时间复杂度是O(logn+nlogn)=0(nlogn) 

public static void test6(int n) {
        for (int i = 1; i < n; i = i * 2) {
            for (int j = 0; j < n; j++) {
                System.out.println("test");
            }

        }

    }

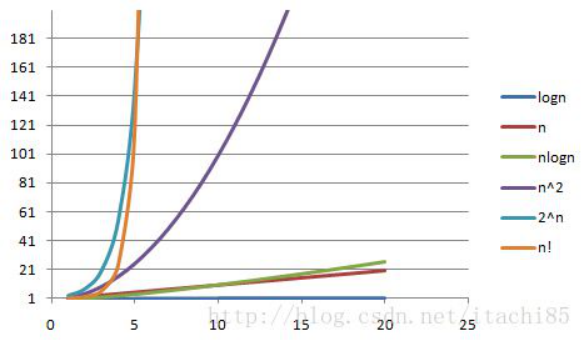
常见时间复杂度的大小（复杂度越小越好）

 

 

 

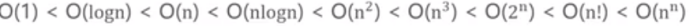
四、算法的优化方向

1. 用尽量少的存储空间
2. 用尽量少的执行步骤(执行时间)
3. 根据情况可以：空间换时间、时间换空间