OO第一单元总结

程序设计思路

第一单元的内容是对表达式的求导，分为三次迭代开发。

第一次的要求是简单多项式的求导，第二次添加了简单的三角函数（函数里仅为x）和表达式因子（可嵌套），第三次添加了三角函数的嵌套形式（函数里为因子）以及判断表达式的合法性。

第一次作业思路

类图

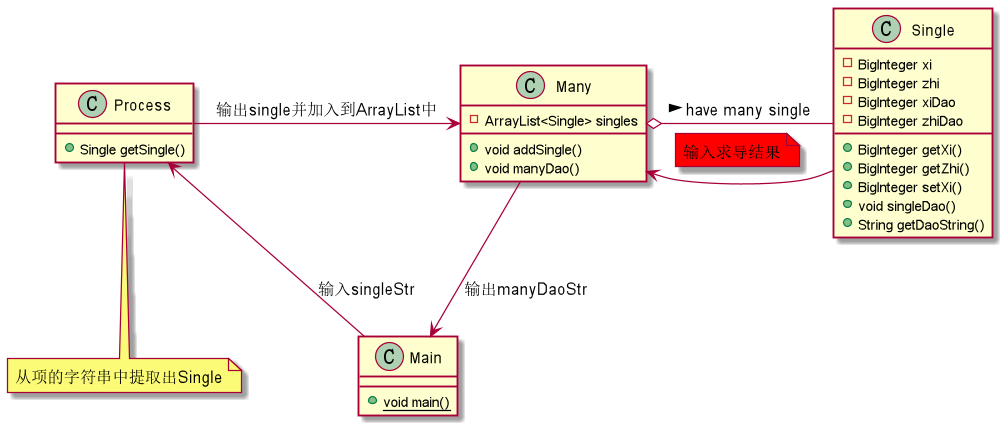
image

  • 由于多项式的每一项有固定的形式：coe*x**index，所以建立一个Single类表示项，再建立一个包含Single的ArrayList容器的Many类表示多项式。
  • 对字符串进行预处理，去除多的符号和空白字符。
  • 由于本次作业较为简单，可以直接用正则表达式提取出项的字符串，再解析出项并加入到Many中（注意合并同类项）。
  • 对多项式求导即对每一个项求导（较为简单故不赘述）并加入到Many的导函数中。
  • 输出时要求拼接每一个单项式的输出得到最终输出。
graph LR 1[主函数读取数据] 2[预处理] 3[解析获取单项式并加入Many] 4[对单项式求导并加入Many中的导函数] 5[输出结果] 1-->2-->3-->4-->5

优缺点

  • 在Single里面设置了Single求导之后的参数，太繁琐，应该直接设一个方法Single getDer()，直接返回Single求导后的项

第二次作业思路

类图

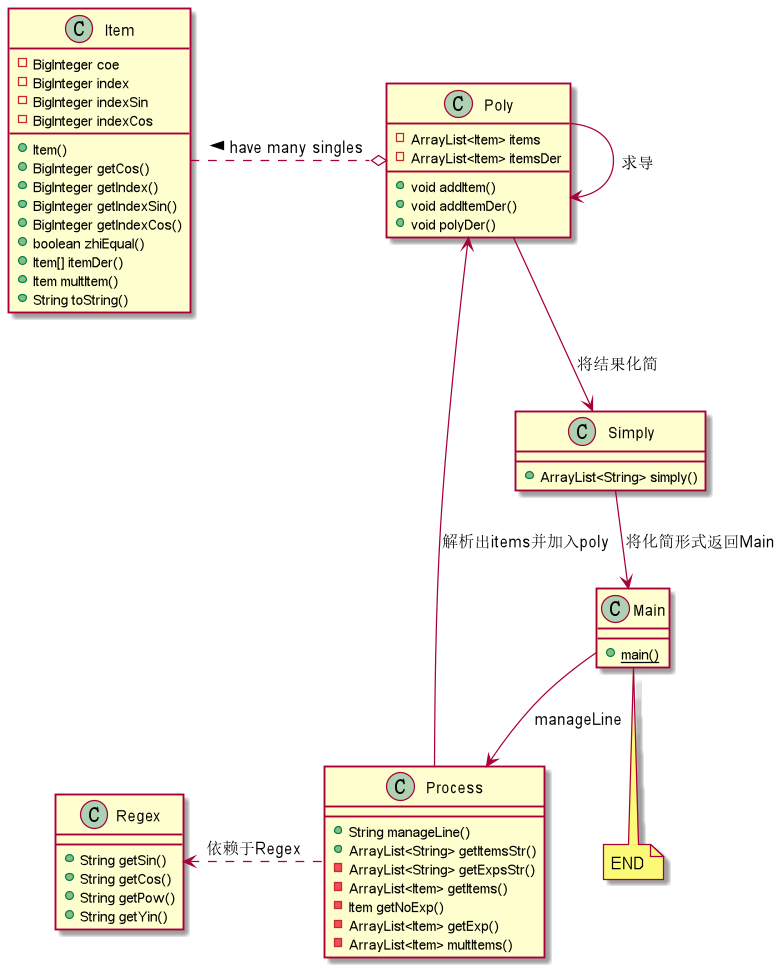
image

  • 由于多项式的每一项有固定的形式：coe*x**index*sin(x)**indexSin*cos(x)**indexCos，所以J建立Item表示项，再建立一个包含Item的ArrayList容器的Poly类表示多项式。

  • 对字符串进行预处理，去除多的符号和空白字符。

  • 由于本次作业包含了表达式因子且能嵌套，故无法由正则表达式取得项的字符串。可以通过直接对字符串处理，获得项的字符串ItemStr。获得字符串后，先提取出表达式因子，再根据正则表达式提取出其中的幂函数和三角函数，得到基础项。若该项不含有表达式因子，则将其添加至Poly中，否则，将表达式因子的项提取出来，相乘化简，直至原项的表达式因子被处理完。

  • 对Poly求导即对每一个项求导（较为简单故不赘述）并加入到Poly的导函数中。

  • 输出时按要求拼接每一个单项式的输出并化简得到最终输出。

    graph TD 1[主函数读取数据] 2[预处理] 3[解析获取ItemStr] 1-->2-->3 3-->conditionA{字符串是否含有表达式因子} conditionA--NO-->4[添加Item至Poly] conditionA--YES-->5[提取表达式因子并相乘化简] 5-->conditionB{原项表达式因子是否处理完} conditionB--YES-->6[添加Items至Poly] conditionB--NO-->5 4-->7[对Poly求导并添加至Poly的导函数] 6-->7[对Poly求导并添加至Poly的导函数] 7-->8[化简并输出结果]

优缺点

  • 直接将项写成coe*x**index*sin(x)**indexSin*cos(x)**indexCos方便了求导，也方便了化简，但是这么写没有考虑到第三次作业的需求，导致第三次作业需要重构。
  • 化简时先考虑sin(x)cos(x)都相同的，再考虑sin(x)cos(x)一个相同，最后考虑x相同的情况，使得最后结果的长度更短。

第三次作业思路

类图

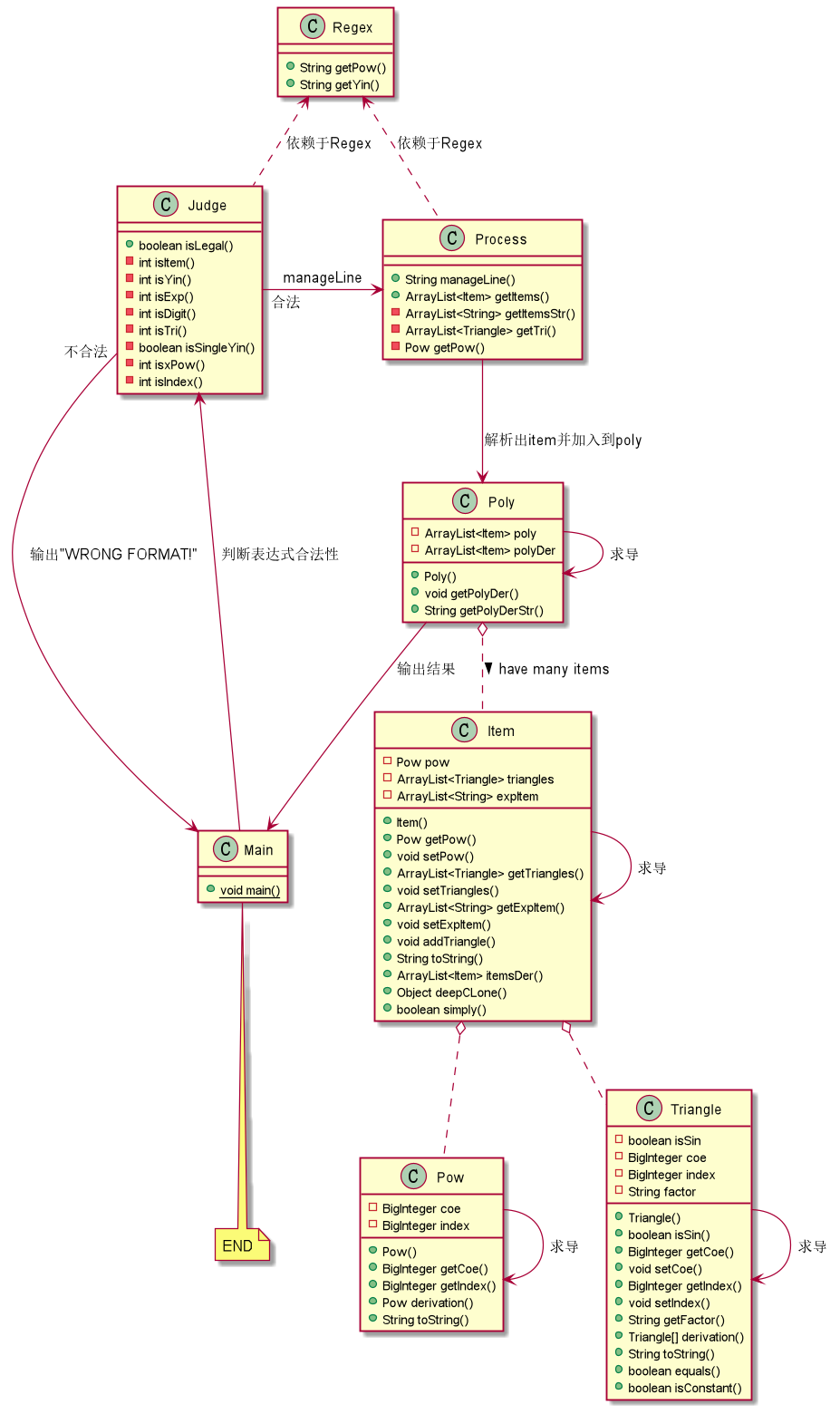
image

  • 由于第三次作业三角函数内是因子，故建立三角函数的类Triangle，幂函数的类Pow两个基础类。项的类Item由一个Pow类、一个ArrayList<Triangle>容器存储三角函数以及一个ArrayList<String>容器存储表达式因子。最后建立一个包含Item的ArrayLIst容器的Poly表示多项式。

  • 本次作业不保证输入表达式的正确性，所以还需要建立一个类Judge判断表达式是否合法。若不合法，直接输出"WRONG FORMAT!"，否则，继续。

  • 对字符串进行预处理，去除多的符号和空白字符

  • 先按照第二次作业的直接处理法，得到项的字符串itemStr。由于三角函数也可能含有表达式因子，故先获取三角函数，接着获取表达式因子，再由正则表达式取得幂函数，最后将Item加至Poly中。

  • 项求导：将Item里面的pow，每一个triangle（去除常量后），每一个expStr（去除常量后）看作一个个体，求导时对其中一个个体求导其余不变，获得一项，最后获得1+n(triangle)+n(expStr)个项组成ArrayList<Item> ItemDers。

  • 对Poly求导即对每一个项求导并将ItemDers加入Poly的导函数中。

  • 输出结果。

    graph TD 1[主函数读取数据] 1-->conditionA{表达式是否合法} conditionA--NO-->2[输出 WRONG FORMAT!] 2-->3[END] conditionA--YES-->4[解析获取itemStr] 4-->5[提取item并添加至Poly] 5-->8[Poly开始求导]-->6[对项求导]-->7[对item其中一个个体求导] 7-->conditionB{item的个体是否处理完} conditionB--NO-->7 conditionB--YES-->conditionC{项是否处理完} conditionC--NO-->6 conditionC--YES-->9[输出结果]-->3

优缺点

  • Pow类和Triangle类有大量相同点，没有用继承关系或接口。
  • Regex类的实际用途很少，应该取消这个类。
  • 最后的表达式没有化简。

基于度量分析程序设计结构

Complexity Metrics

  • ev(G)：基本复杂度——衡量程序非结构化程度

  • iv(G)：模块设计复杂度——衡量模块判定结构，即模块与其他模块的调用关系

  • v(G)：圈复杂度——衡量模块判定结构的复杂程度，数量上表现为独立路径的条数

  • OCavg：类的方法的平均循环复杂度

  • WMC：类的总循环复杂度

第一次作业Complexity

Method ev(G) iv(G) v(G)
Main.main(String[]) 1 2 2
Many.addSingle(Single) 5 5 5
Many.manyDao() 4 4 5
Process.getSingle(String) 1 10 10
Single.Single(BigInteger,BigInteger) 1 1 1
Single.getDaoString() 1 11 11
Single.getXi() 1 1 1
Single.getXiDao() 1 1 1
Single.getZhi() 1 1 1
Single.getZhiDao() 1 1 1
Single.setXi(BigInteger) 1 1 1
Single.setZhi(BigInteger) 1 1 1
Single.singleDao() 1 3 3
Class OCavg OCmax WMC
Main 2 2 2
Many 5 5 10
Process 10 10 10
Single 2.22 11 20

分析上面数据，我们可以看出Process.getSingle()和Single.getDaoStr()的模块设计复杂度高，原因是在获取Single项和输出结果字符串时，使用了大量的if判断语句和调用其他模块，使得复杂度提高，也使得代码难以测试和维护。

从循环复杂度方面来说，Process类需要处理字符串，故其复杂度较高。

第二次作业Complexity

Method ev(G) iv(G) v(G)
Item.Item(BigInteger,BigInteger,BigInteger,BigInteger) 1 1 1
Item.getCoe() 1 1 1
Item.getIndex() 1 1 1
Item.getIndexCos() 1 1 1
Item.getIndexSin() 1 1 1
Item.itemDer() 1 1 1
Item.multItem(Item) 1 1 1
Item.toString() 2 13 16
Item.zhiEquals(Item) 1 4 4
Main.main(String[]) 1 3 3
Poly.addItem(Item) 4 6 6
Poly.addItemDer(Item) 4 6 6
Poly.derToString() 2 2 3
Poly.getItemsDer() 1 1 1
Poly.polyDer() 4 7 8
Process.getExp(String) 1 4 4
Process.getExpsStr(String) 1 5 6
Process.getItems(String) 1 3 3
Process.getItemsStr(String) 1 13 16
Process.getNoExp(String) 1 11 11
Process.manageLine(String) 1 1 1
Process.multItems(ArrayList,ArrayList) 1 3 3
Regex.getCos() 1 1 1
Regex.getPow() 1 1 1
Regex.getSin() 1 1 1
Regex.getYin() 1 1 1
Simply.getCosArr(int,ArrayList,ArrayList) 1 11 11
Simply.getCosStr(ArrayList) 1 3 3
Simply.getSinArr(int,ArrayList,ArrayList) 1 11 11
Simply.getSinCosArr(int,ArrayList,ArrayList) 1 10 10
Simply.getSinCosStr(ArrayList) 1 5 5
Simply.getSinStr(ArrayList) 1 3 3
Simply.getXArr(int,ArrayList,ArrayList) 1 8 8
Simply.getXStr(ArrayList) 1 3 3
Simply.inItem(ArrayList,Item) 3 2 3
Simply.mergeStr(ArrayList) 1 3 3
Simply.simply(ArrayList) 1 12 12
Class OCavg OCmax WMC
Item 2.44 14 22
Main 3 3 3
Poly 3.6 6 18
Process 5.71 14 40
Regex 1 1 4
Simply 4.64 11 51

第二次作业中Item.toString()需要考虑各种可能性，判断语句用的多，复杂度提高；Process.getItemsStr(String)，Process.getNoExp(String)都是从字符串中提取相应的项，复杂度高；Simply.getCosArr(int,ArrayList,ArrayList)，Simply.getSinArr(int,ArrayList,ArrayList)，Simply.getSinCosArr(int,ArrayList,ArrayList)，Simply.simply(ArrayList)都是搜寻同类项，需要进行判断，故复杂度较高。

与第一次作业相比，由于第二次作业更复杂，所以总的循环复杂度提高了，但是类的平均循环复杂度减小了，可以看出代码质量是有一定的提高的。

第三次作业Complexity

Method ev(G) iv(G) v(G)
Item.Item(Pow,ArrayList,ArrayList) 1 1 1
Item.addTriangle(Triangle) 4 4 5
Item.deepCLone() 1 1 1
Item.getExpItem() 1 1 1
Item.getPow() 1 1 1
Item.getTriangles() 1 1 1
Item.itemsDer() 5 7 7
Item.setExpItem(ArrayList) 1 1 1
Item.setPow(Pow) 1 1 1
Item.setTriangles(ArrayList) 1 1 1
Item.simply() 4 7 7
Item.toString() 1 14 14
Judge.isDigit(String,int) 8 9 12
Judge.isExp(String,int) 7 5 7
Judge.isIndex(String,int) 9 7 11
Judge.isItem(String,int) 11 10 14
Judge.isLegal(String) 13 13 20
Judge.isSingleYin(String) 4 5 7
Judge.isTri(String,int) 8 8 11
Judge.isYin(String,int,boolean) 16 22 23
Judge.isxPow(String,int) 2 2 2
Main.main(String[]) 1 2 2
Poly.Poly(ArrayList) 1 3 3
Poly.getPolyDer() 1 5 5
Poly.getPolyDerStr() 2 3 4
Pow.Pow(BigInteger,BigInteger) 1 1 1
Pow.derivation() 2 2 2
Pow.getCoe() 1 1 1
Pow.getIndex() 1 1 1
Pow.toString() 2 3 3
Process.getItems(String) 9 13 13
Process.getItemsStr(String) 1 13 16
Process.getPow(String) 2 9 9
Process.getTri(ArrayList) 7 8 10
Process.manageLine(String) 1 1 1
Process.merge(ArrayList) 1 7 8
Process.replace1(String,String) 3 3 3
Regex.getPow() 1 1 1
Regex.getYin() 1 1 1
Triangle.Triangle(boolean,BigInteger,BigInteger,String) 1 1 1
Triangle.derivation() 2 3 3
Triangle.equals(Object) 3 6 7
Triangle.getCoe() 1 1 1
Triangle.getFactor() 1 1 1
Triangle.getIndex() 1 1 1
Triangle.isConstant() 1 2 2
Triangle.isSin() 1 1 1
Triangle.setCoe(BigInteger) 1 1 1
Triangle.setIndex(BigInteger) 1 1 1
Triangle.toString() 2 3 4
Class OCavg OCmax WMC
Item 3.17 12 38
Judge 8.89 16 80
Main 2 2 2
Poly 4 5 12
Pow 1.6 3 8
Process 7.57 14 53
Regex 1 1 2
Triangle 1.64 4 18

第三次作业中新增了基础类Pow和Triangle，还有表达式合法性判断的类Judge。其他类的复杂度与第二次作业类似。Judge类中的方法大都涉及到字符串的判断问题，所以复杂度高。

可以看出，由于item不再是基础项，所以平均循环复杂度提高了。其中Judge的循环复杂度无论平均还是总的，都是最高的。高的复杂度在后面的debug中带给了我很大的痛苦。

Dependency Metrics

  • Cyclic：和类直接或间接相互依赖的类的数量。
  • Dcy和Dcy*：该类直接依赖的类的数量，带*包括了间接依赖。
  • Dpt和Dpt*：直接依赖该类的数量，带*包括了间接依赖

第一次作业Dependency

Class Cyclic Dcy Dcy* Dpt Dpt*
Main 0 3 4 0 0
Many 0 1 1 1 1
Process 0 2 2 1 1
Single 0 0 0 3 3

第二次作业Dependency

Class Cyclic Dcy Dcy* Dpt Dpt*
Item 0 0 0 4 4
Main 0 4 5 0 0
Poly 0 1 1 1 1
Process 0 2 2 1 1
Regex 0 0 0 1 2
Simply 0 1 1 1 1

第三次作业Dependency

Class Cyclic Dcy Dcy* Dpt Dpt*
Item 3 4 6 4 4
Judge 3 2 6 2 4
Main 0 4 7 0 0
Poly 3 3 6 2 4
Pow 0 0 0 3 5
Process 3 5 6 4 4
Regex 0 0 0 1 5
Triangle 0 0 0 2 5

可以看到，第一次和第二次都没有出现互相依赖的情况，第三次由于程序的复杂出现了互相依赖的情况，这会增加系统的复杂性，不利于代码的维护，往往会牵一发而动全身。

分析自己程序的bug

第一次作业bug

  • 错误样例1：0000*x**1234*x**123+000*x**12*23*34*45+-000*x**-03*x**-04

  • 错误原因：在输出结果字符串时，忽略了0这种情况，导致程序没有输出

  • 错误样例2：--8 * -443795535622748304+ -5652858511874 *-567324* +1570+- +1814103387*x ++69523438539396* -10920350092417 - + -9 *x *x* x++ +1052-x --8000

  • 错误原因：在进行字符串预处理时，忽略了两项直接可能存在的符号数为三个，分别是项的符号，因子的符号，还有常数因子的符号。

第二次作业bug

  • 错误样例1：--+07783x**1+-+03456789x**3+ x**1*(- -+675*x**2+sin(x)**-02+ -33*x**2)
  • 错误原因：在判断项的正负时，例如-x形式时，还需要判断-号之后是否为数字，判断时将">=0&&<=9"写成了">0&&<9"，导致项的正负号出现了问题。

第三次作业bug

  • 错误样例1：+6*cos((cos(x)*x++1*(x**+0*x*7-+x*x**+8*sin(+ 030))))**+7*x

  • 错误原因：在判断三角函数里面的是否为因子时，首先是先判断其中式子的合法性，之后再对字符预处理。问题就出在这里，+ 030这种形式作为表达式是合法的，预处理后变成了+030作为因子也是合法的，但是开始的+ 030不是因子。所以这里不能直接预处理，而应该使用String.trim()去除式子头尾的空白字符即可。

  • 错误样例2：sin((x+sin(x)*(1-sin(x)+sin((x))**-1)-cos(x)**2))+sin(x)*cos(x)**-1

  • 错误原因：问题出在sin(x)*cos(x)**-1，该式求导后会出现一项cos**0，这一项被加入到ArrayList<Triangle>中后是不会输出的（值为1故不输出），所以在求导后的结果加入至ArrayList需要考虑index是否为0.

bug分析

Method ev(G) iv(G) v(G)
Process.getNoExp(String) 1 11 11
Item.simply() 4 7 7
Judge.isSingleYin(String) 4 5 7
Class Cyclic Dcy Dcy* Dpt Dpt*
Item 3 4 6 4 4
Judge 3 2 6 2 4

第二次作业的bug位于Process.getNoExp()中，第三次作业bug位于Judge.isSingleYin()和Item.simply()中。

从上面的表格可以看到，Process.getNoExp()的iv(G)高，这意味着模块耦合度高，v(G)高意味着圈复杂度高，这使得代码不易读且难以自测，第二次作业的bug就出在这里也就情有可原了。

对于Item.simply()和Judge.isSingleYin()，ev(G)相对较高，意味着非结构化程度较高，且Item和Judge类和其他类有相互依赖的关系，这就会使得自测难以发现问题。

在以后的程序编写中，要注意”高内聚，低耦合“的思想。

如何有效的发现别人的bug

在互测环节，由于时间关系，我只在第二次作业中提交了数据，还没有hack到人。经过这几天的分析，我认为有效地hack别人的代码需要以下几点。

  • 构造功能测试集：对于每一个可能的存在的问题，比如说嵌套，符号问题，常量问题都构造数据，测试其基本功能。
  • 构造极限测试集：对于大类数，0 等特殊情况构造数据，测试其边界功能是否完备。
  • 压力测试：在符合允许的最大字符数的情况下尽可能多。

心得体会

本单元的学习，可以算是我的java学习入门之旅。从一开始啥也不会到现在的会一点点，可以说是迈出了我的第一步。虽说如此，但在本单元的学习中，还是存在很多的不足，比如说继承、接口等关系都没有使用，用的最多的容器还是偏向于数组的容器ArrayList，总感觉自己的程序还是披着”面向对象“外衣的面向过程程序，希望在接下来的几个单元的学习中，能够真正做到面向对象。

posted @ 2021-03-26 16:50  ZHL3105645  阅读(82)  评论(0)    收藏  举报