对三次PTA大作业的总结—— BLOG_1
面对对象程序设计---PTA前三次作业总结
引言:这次的命题人是蔡柯老师,不同与初学c语言,这类java一改我对编程题的认识。想来十分有意义,总结这段时间的做题体会。
PTA大作业一
前言:这次的作业主要考察基础的java程序的设计,在有效运用课本上的知识的同时,又别出心裁的涉及到一些老师上课没有讲到而需要自学的一些知识,课堂课外知识的巧妙结合,既考察了上课知识的吸收率,又给我们一些课外的学习时间。题目集一共有十道,主要考察了对输入输出的应用和基本判断,循环语句分支的使用。包含一些Java编程常用方法和技巧。总体来说题目难度偏易,适合初学,作为第一次作业可以强化我们对java语言结构和编码的基础。不过这题目也是易中有难,实现题目功能很快,但是有些测试点需要通过却需要调试去调整代码的运行逻辑。
各题目 设计与分析 踩坑心得 改进意见 核心代码分析:
(1)题目集1:7-7 三角形类型的判断
设计与分析:

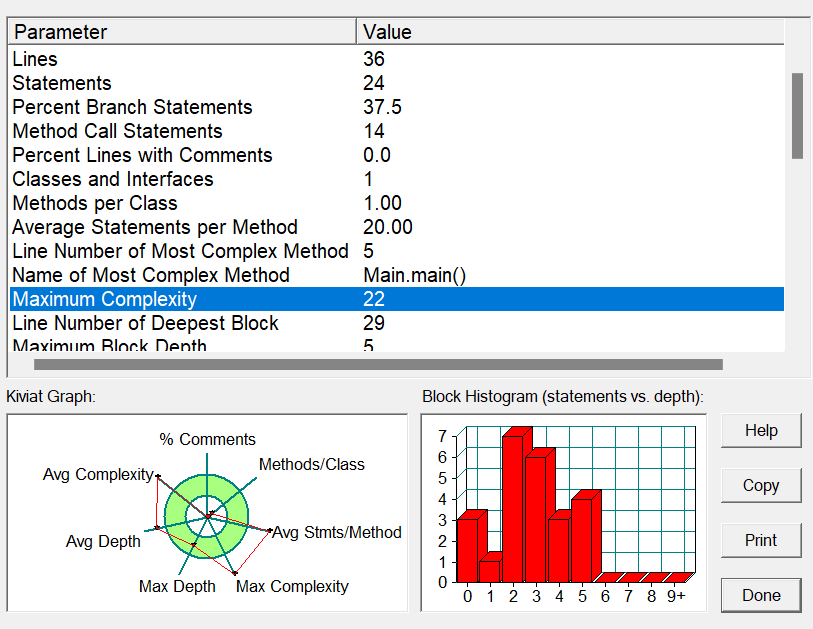
因该题比较简单,不需要构建类去完成,只需要在main函数中实现函数的全部功能,首先通过判段对输入的数据进行检验,再通过一系列的if/else语句去判断三边满足的关系,得出初步结论,再通过一系列的判断语句得出题目的结果,最后再将判断的结果输出,虽然形式简单,但还是出现了测试点的调试,以下简述我的踩坑心得。
踩坑心得:

以上代码为判断是否是直角三角形,涉及到对直角三角形的判断,都需要用勾股定理对三角形进行判断。
但是采取a*a+b*b=c*c会导致对直角三角形的判断出错,这是由于double类型的数在平方后精度丢失,导致勾股定理的等式判断出错,输出错误的答案。
正确的做法是采用Math.abs(a*a+b*b-c*c)<0.00001,这里涉及到对两个double类型数据的相等的比较,由于java类似中double类似精度的独特算法,面对这种情况就需要对两个数据的差精度比较,只要精度小于0.00001,就可以说明这两个数据是相等的。这种技巧是一种常用的技巧,需要我们记住。
这个坑浪费了我很多时间,后来发现是对java中double类型数据的认识错误,这就导致了我对这道题记忆犹深。这就告诉我们要理解事情的本质,而不要陷入思维固化中。
改进意见:
1.由上图可知,这个代码的圈复杂度达到了22,这说明代码的质量不高。因为我在写题目的过程中,只注意需要完成题目要求的功能,而没有对代码进行优化,导致写了过多的if/else语句,据查找资料,if/else 和循环的使用会使得圈复杂度提高,改进的方法是将if/else语句换成switch语句,可以有效减少圈复杂度。
2.可以先排序找出三边长度的大小的的小,在使用勾股定理时就可以有效地减少判断,提高代码的质量。
3.可以将判断的逻辑颠倒过来,这样代码的思路就会更加的清晰,代码的可读性也会更高。
核心代码分析:
public class Main{
public static void main(String []args)
{
Scanner input = new Scanner(System.in);
//获取输入
double a = input.nextDouble();
double b = input.nextDouble();
double c = input.nextDouble();
//判断是否输入非法
if(a<1||a>200||b<1||b>200||c<1||c>200)
System.out.println("Wrong Format");
else
{
if(a+b<=c||a+c<=b||b+c<=a)//是否能构成三角形
System.out.println("Not a triangle");
else if(a != b &&b !=c &&c != a) //是否三边不相等
{
if(((a*a+b*b)==c*c)||((b*b+c*c)==a*a)||((a*a+c*c)==b*b))
System.out.println("Right-angled triangle");//是否是直角三角形
else
System.out.printf("General triangle");//是否是一般三角形
} else if(a == b && b ==c && c==a)
System.out.println("Equilateral triangle"); else if((a==b)||(a==c)||(b==c)) //是否是等边三角形
{ if(a!=b||a!=c||b!=c)
System.out.println("Isosceles triangle"); //是否是等腰三角形
if (Math.abs(a*a+b*b-c*c)<0.00001||Math.abs(a*a+c*c-b*b)<0.00001||Math.abs(c*c+b*b-a*a)<0.00001) //是否是等腰直角三角形
System.out.println("Isosceles right-angled triangle"); }
}
}
}
PTA大作业二
前言:题目集二的题量是三道题,难度比题目集一上升了一个档次,这就体现了出题人的良苦用心,题目的难度循序渐进,给我们缓冲和提高的时间,也符合学习的规律。这次题目最难的是7-2。遇到这样的题目确实是头一次,这就叫我必须要一步一步地去构架代码的框架,而不是能直接实现题目的功能。这次作业的用时在四个小时左右,题目在抽象的同时也具备一定的趣味性和真实性,增加了我们对题目的理解,这也为我们解题时带来了一定幅度的增益,把抽象的的题目具体化,再细化到每一行的代码中去。
各题目 设计与分析 踩坑心得 改进意见 核心代码分析:
(1)7-2 串口字符解析
设计与分析

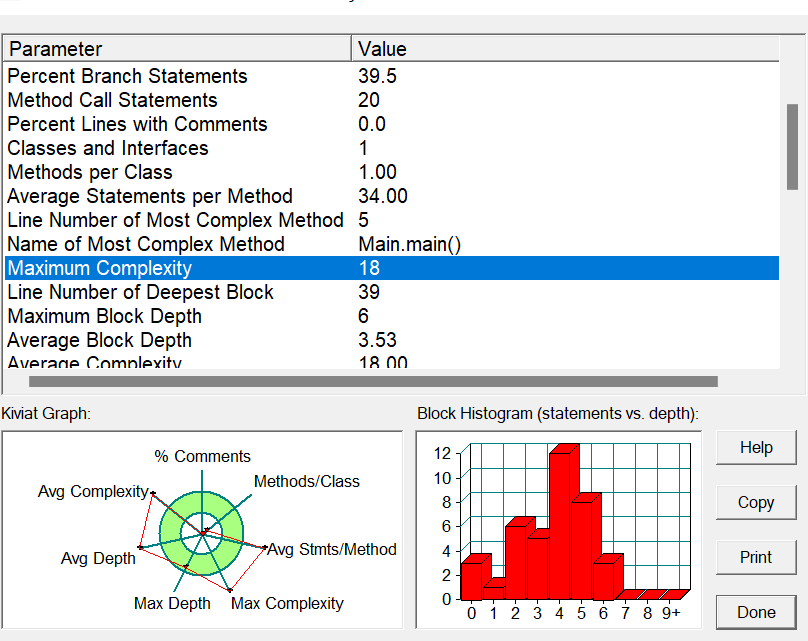
该题的难度在于理解题目本身,上来一串二进制数组就让我们头晕眼花,这道题目我看了有半个小时,在测试样例的帮助下了解题目。
由于该题我理解了很久,那我就把这道题目的理解写下来。
在异步通信模式下,串口可以一次发送5~8位数据
收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位)
发送方有数据发送时,会在有效数据(5~8位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”
这题难度之一就是理解有效数据,在空闲位结束时会发送起始位0 ,之后有八位有效数据,有效数据后接着一位奇偶校验位和结束符1。
理解奇偶校验位是本题解题的关键。
我开始以为奇偶校验位为1是就是奇校验位,为0就为偶校验。
但是样例告诉我我的理解错误。
在看完全部样例之后,我知道了八位有效数据再加上奇偶校验位一共九位数中出现奇数个1则为奇校验,反之为偶校验。
踩坑心得:
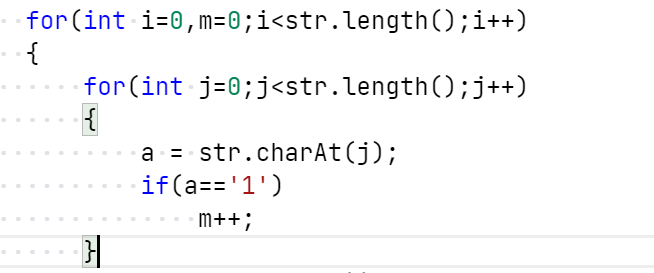
这一段代码是统计有效数据中1的个数,在第一次判断正确,而之后的校验位就会出错,这表明代码出现了bug,在一段时间的调试后发现问题所在:
这个题目错在第二次再判断时未将计数m归为零,导致校验位出现了错误。这是我写代码的习惯不会导致,如果书写规范,就不会出现这种会影响结果又难以发现的问题上。
这也是一个逻辑上的疏忽,别看只是少了一句话,而带来的程序的运行错误。这告诫我书写程序时需要思维缜密,注意力集中,少受别人的干扰。
改进意见:
1、由上图分析,这道题的圈复杂度为22,超过了15,这表明代码的质量还可以提高,这道题是由于写了很多个循环的结果导致。其实有些循环可以把他合并起来,这样既减少了代码的行数,又提高了代码的质量。
2、这题没用使用一个类,其实可以将输入的数据的子字符串写成一个类,这样就打打提高了代码的执行时间和复杂程度。
3、通过对后续知识的学习,如果采用动态的数组可以规避字符串在访问时的越界访问。
核心代码分析:
public class Main{
public static void main(String []args){
Scanner input = new Scanner(System.in);
String str = input.nextLine();
char a,b;
int flag=0;
for(int i=0,m=0;i<str.length();i++)
{
for(int j=0;j<str.length();j++)
{
a = str.charAt(j);
if(a=='1')
m++; //计算1的数量
}
if(str.length()<11||m==str.length()) //判断输入是否非法
{
System.out.println("null data");
break;
}
else{
flag=1; //输入正确,flag为标志位
break;
}
}
for(int i=0,n=0,p=1;i+10<str.length()&&flag==1;i++)
{
a = str.charAt(i);
if(a=='0') //寻找起始位
{
String s = str.substring(i+1,i+11);//截取十位字符串
for(int j=0;j<9;j++)
{
b = s.charAt(j);
if(b=='1') //寻找结束位
{
n++; //统计1的位数
}
}
if(n%2!=0) //是否为奇校验
{
if(s.substring(9,10).equals("1"))
{
System.out.printf("%d:%s\n",p,s.substring(0,8)); //输出有效数据
}
else
{
System.out.printf("%d:validate error\n",p);
}
}
else{
if(s.substring(9,10).equals("1"))
System.out.printf("%d:parity check error\n",p);//格式化输出
else
System.out.printf("%d:validate error\n",p);
}
p++;
i+=10;
n=0; //把校验位赋值为零
}
}
}
}
PTA大作业三
前言:作业三的难度陡然提高,让我措手不及,也让我开了眼界。这次题量还是三道题,但是这个题的质量跟前两次的作业不在一个档次。难度:难。全部写完时间超过十个小时,代码量也轻易超过了百行。其中的算法和逻辑难度也相对复杂。这题目上手难度低,但是每道题从不到10%的正确率也可以说明这些题目通过确实不易,因为代码长起来之后就不容易debug,这对逻辑的考验,和对算法的理解,都成为了能否写出这些题目的关键。这三道题目刷新了我对java题目的认识,也说明我写的题目确实少,需要改进。
各题目 设计与分析 踩坑心得 改进意见 核心代码分析:
(1)7—1 计算两点间的距离
设计与分析:

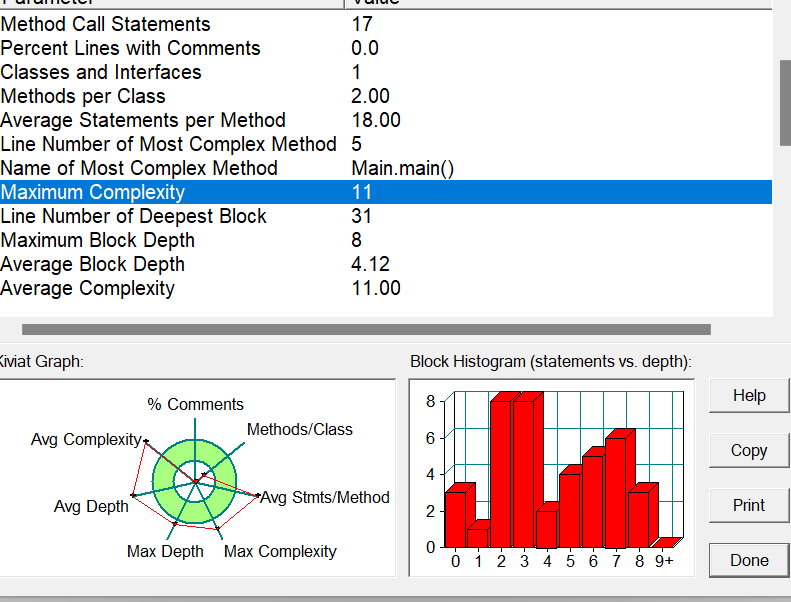
如果你觉得这道题很简单那就是被这道题的表面给迷惑了,确实,只需要运用两点间的距离公式就可以实现这道题的算法;
可是这道题的输入检测却非常的影响人的心态,这道题我提交了八十多次,我数的时候也被我自己给震惊了。这道题困扰了我两天才通过了其中的测试点。
这题只需要用一个String的字符串去接收题目中的输入,再使用String中的方法spilt将字符串进行拆分,再转化成double类型的数据就可以解决这道题的。
踩坑心得:
这题所有的坑都来自非法输入(以下是我对于输入非法的一些样例)
1:+-2,001 3,1
2: 02.,3 1,2,3
3: 1+2,-0 1,2 (末尾有空格)
4:1, 1,,2
这题我被反复折磨,其实就是做重复的事情,由于没有提示测试样例的点,那我只能一步一步地去尝试。
在经过大量输入之后,我总结了以上的输入非法并对代码进行改进,直到通过所有的测试点。其中的难受真的时不想体验第二遍。
改进建议:
1、由图可知,该题的圈复杂度为11。这里有点可惜,如果小于10代码质量就会很好。改进可以减少循环的使用。
2、这题可以将获取字符串变成一个字符数组。
3、此题可以将split方法改进,提高程序的执行效率
核心代码分析:
if(s.length==4) { //字符数组的长度正确
loop:for(int i=0;i<4;i++) {
if(s[i].length()==0){ //数组为空
System.out.println("Wrong Format");
break;
}
loop: for(int j=0;j<s[i].length();j++) {
char ch = s[i].charAt(j);
if((ch>='0'&&ch<='9')||ch=='.'||ch=='-'||ch=='+') {
flag=1; //设立标志位为1
if((ch=='+'||ch=='-'||ch=='.'||ch=='0')&&j+1<s[i].length()) { //判断输入流是否输入非法
char ch1 = s[i].charAt(j+1);
if (ch1=='.')
break;
if(ch1<='0'||ch1>'9') { //判断非法字符
flag = 0;
System.out.println("Wrong Format");
break loop;//退出双重循环
}
}
else if(ch<'0'||ch>'9'||j+1>s[i].length()){//输入非法字符
flag = 0;
System.out.println("Wrong Format");
break loop;
}
}
else {
System.out.println("Wrong Format");
flag = 0;
break loop;
}
}
}
}
(2)习题7—2 点线形系列2-线的计算
设计与分析:


这道题涉及到的非法输入同第一题,只有稍微改变。
这到题涉及到几何知识,给出的是二维坐标的点,一共分成了1-5个点,1-4中计算斜率,判断点是否在直线上,判断直线是否平行,这只需要根据斜率的计算进行判断就可以。
5涉及到的是两个直线的交点问题,我运用线性代数中求解方程解的方法来进行计算,第四题最难的点在于如何判断两条线段是否会相交。在下面的踩坑心得给出。
踩坑心得:
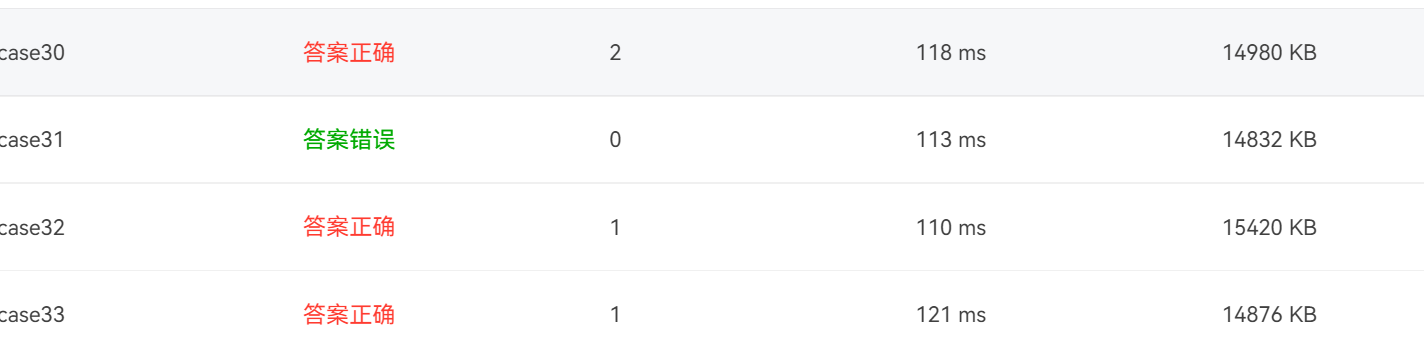
这是case31错误时的截图,这道题这个点我也是测试了非常久才给出了正确的答案。
原因在于一个函数

我在网上学习了如何判断两条直线是否相交的函数java.awt.geom.Line2D.linesIntersect 去判断直线是否相交,但是这个函数在实现时考虑到了端点,而本题要求不考虑端点,这就导致了这个函数出了问题
于是我想到非常关键的一步,修改本题的逻辑顺序,从直线不相交的情况开始判断,那么只需要在else中排除端点就可以了,而端点的排除本身并不复杂,这就修改了本题的逻辑问题,代码通过case31
改进意见:
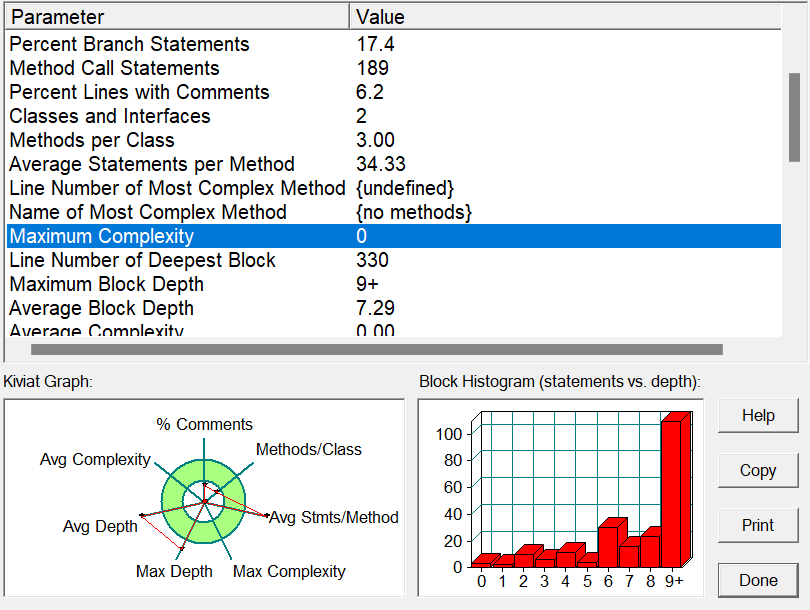
1、如复杂度分析图所示,本题的圈复杂度为33,超过了代码的一般范围,这就意味这该代码的可读性非常的差,而对与前文提到的方法都可有效减少圈复杂度。
2、本题的代码有两百多行,代码的简化就显得尤为重要,应该适当的合适代码的逻辑,让代码模块化。
3、如果能够将代码的逻辑颠倒一下,程序将更加的合理。
核心代码如下:
else if(a==5) {
if(Math.abs(k(x1,y1,x2,y2)-k(x3,y3,x4,y4))<0.00001) {
System.out.println("is parallel lines,have no intersection point");
}
else {
double a1 = y2- y1;
double b1 = x1 - x2;
double c1 = x1*y2 - x2*y1;
double a2 = y4 - y3;
double b2 = x3 - x4;
double c2 = x3*y4 - x4*y3;
double det= a1*b2 - a2*b1;
double x0 = (c1*b2 - c2*b1)/det;
double y0 = (a1*c2 - a2*c1)/det; //交点坐标公式 线性代数
if((x0==x1&&y0==y1)||(x0==x2&&y0==y2)||(x0==x3&&y0==y3)||(x0==x4&&y0==y4)){ //判断交点就是线段的端点
System.out.println(x0+","+y0+" "+"false");
}
else if(!java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x3, y3, x4, y4)) {
if(x1==Math.max(Math.max(x2, x3),Math.max(x2, x4))||x1==Math.min(Math.min(x2, x3),Math.min(x2, x4)))//排除端点 case31
System.out.println(x0+","+y0+" "+"false");
else
System.out.println(x0+","+y0+" "+"true");
}
else {
System.out.println(x0+","+y0+" "+"true");
}
}
}
(3)7—3 点线形系列3-三角形的计算
设计与分析:

这道题变成了对三角形的判断 获取输入后先要判断输入的数据是否能构成三角形 由于使用次数的比较频繁,写成了一个static 方法
还是1-5个功能 1-3判断三角形的类型 计算三角形的面积 周长 重心坐标这三个都比较的简单 不进行赘述
4是判断一条直线与一个三角形的交点个数 这个功能的情况就非常多了,判断是否能构成直线 是否构成三角形 如何求交点的个数
这个我也是通过写静态方法的方式去实现这个功能
5是判断点的位置,题目要求必须使用射线法,所谓射线法,通过一段时间的学习了解并实现
从点开始向左(以向左为例)引出一条射线,计算这条射线与三角形的交点个数,由于射线的特殊性,只有交点为奇数时在三角形的内部,交点为偶数时在三角形的外部。
但是由于截至时间的限制,我没有通过这到题 这题得分30/48。
踩坑心得:
(1)如何求三角形被直线分割后的面积
三角形被直线分割后,会变成一个四边形和一个三角形,思路是用分割前的三角形减去分割后的三角形,但是如何定位小三角形的第三个点呢?

由画图后知道,直线切割只有三种情况,只要确定了直线和三角的的那两边相交,就可以定位三角形的在哪里。
(2)如何根据题目要求输出
输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
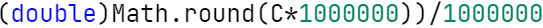
采取的是使用Math.round函数去四舍五入 先将要输出的数扩大六位,四舍五入后再除掉六位,转化为double类型的数,就得以得到题目要求的输入
改进意见:
1、代码的有些语句判断过长,可以将其拆分,增强观感
2、注意到,本题代码的圈复杂度为零,圈复杂度为零代表本体代码可读,我怀疑是软件测评出现了问题
核心代码分析:
(1)选项4
if(a==4) {
x1 = Double.parseDouble(s[0]);
y1 = Double.parseDouble(s[1]);
x2 = Double.parseDouble(s[2]);
y2 = Double.parseDouble(s[3]);
x3 = Double.parseDouble(s[4]);
y3 = Double.parseDouble(s[5]);
x4 = Double.parseDouble(s[6]);
y4 = Double.parseDouble(s[7]);
x5 = Double.parseDouble(s[8]);
y5 = Double.parseDouble(s[9]);
if(x1==x2&&y1==y2)
System.out.println("points coincide");
else if(is_trianger(x3,y3,x4,y4,x5,y5)) {//是否能构成三角形
double S0 = area(x3,y3,x4,y4,x5,y5),S1=0;
int count = 1;//计算交点个数
point p = new point();
point q = new point();
if((k(x1,y1,x2,y2)==k(x3,y3,x4,y4)&&k(x1,y1,x3,y3)==k(x2,y2,x4,y4))||(k(x1,y1,x2,y2)==k(x3,y3,x5,y5)&&k(x1,y1,x3,y3)==k(x2,y2,x5,y5))||(k(x1,y1,x2,y2)==k(x4,y4,x5,y5)&&k(x1,y1,x4,y4)==k(x2,y2,x5,y5)))//重合
System.out.println("The point is on the edge of the triangle");
//直线与三角形相交有两个交点由三种情况,分情况判断即可
else if(java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x3, y3, x4, y4)&&java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x3, y3, x5, y5)) {
p = conpoint(x1, y1, x2, y2, x3, y3, x4, y4);q =conpoint(x1, y1, x2, y2, x3, y3, x5, y5);
S1 = area(p.x,p.y,q.x,q.y,x3,y3);
count =2;
}
else if(java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x3, y3, x5, y5)&&java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x4, y4, x5, y5)) {
p = conpoint(x1, y1, x2, y2, x3, y3, x5, y5);q =conpoint(x1, y1, x2, y2, x4, y4, x5, y5);
S1 = area(p.x,p.y,q.x,q.y,x5,y5);
count =2;
}
else if(java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x3, y3, x4, y4)&&java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x4, y4, x5, y5)) {
p = conpoint(x1, y1, x2, y2, x3, y3, x4, y4);q =conpoint(x1, y1, x2, y2, x4, y4, x5, y5);
S1 = area(p.x,p.y,q.x,q.y,x4,y4);
count =2;
}
if(S1==0) {
count =1;
}
if(count==2) {
double S2 =S0-S1;
if (S1>=S2) {
System.out.println(count+" "+(double)(Math.round(S2*1000000))/1000000+" "+(double)(Math.round(S1*1000000))/1000000);
}
else {
System.out.println(count+" "+(double)(Math.round(S1*1000000))/1000000+" "+(double)(Math.round(S2*1000000))/1000000);
}
}
else
System.out.println(count);
}
else
System.out.println("data error");
}
(2)选项5
if(a==5) {
x1 = Double.parseDouble(s[0]);
y1 = Double.parseDouble(s[1]);
x2 = Double.parseDouble(s[2]);
y2 = Double.parseDouble(s[3]);
x3 = Double.parseDouble(s[4]);
y3 = Double.parseDouble(s[5]);
x4 = Double.parseDouble(s[6]);
y4 = Double.parseDouble(s[7]);
if(is_trianger(x2,y2,x3,y3,x4,y4)) {
int A = inarea(x1,y1,x2,y2,x3,y3,x4,y4);
if(A==2)
System.out.println("in the triangle");
else if(A==1)
System.out.println("on the triangle");
else
System.out.println("outof the triangle");
}
else {
System.out.println("data error");
}
}
static double area(double x1,double y1,double x2,double y2,double x3,double y3) {//计算面积
double x,y,z;
x = Math.sqrt(Math.abs((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)));
y = Math.sqrt(Math.abs((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)));
z = Math.sqrt(Math.abs((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3)));
double S = 0.25*Math.sqrt((x+y+z)*(x+y-z)*(x+z-y)*(z+y-x));
return S;
}
static int inarea(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) { //判断是否在区域内
if(x1<=Math.max(Math.max(x2, x3),Math.max(x2, x4))&&x1>=Math.min(Math.min(x2, x3),Math.min(x2, x4)));{
if(y1<=Math.max(Math.max(y2, y3),Math.max(x2, x4))&&y1>=Math.min(Math.min(y2, y3),Math.min(y2, y4))) {
return 2;
}
else
return 1;
}
}
学习心得:
1、通过三次作业的练习,强化了我对java语言的使用和理解
2、学习了很多编程时使用的技巧和方法
3、深化了我书写代码时的逻辑理解和对算法的实现能力
4、拔高了我对程序设计的眼界和深度
5、领悟自上而下逐步细化的编程思想更加的透彻
6、知道了写程序时细节决定成败,必须一丝不苟
7、让我对自己的水平有了一定的认知,提醒我今后的学习还有很多改进的地方
8、深刻了解了关于Java程序结构和代码书写的规范,以及要遵守的代码书写规范
9、积累了一些debug的经验,深刻认识到了调试的重要性,学会了调试的基本技巧,如何设置断点,单步进入,跟踪参数,以及更改代码的逻辑顺序,排除逻辑错误,对提高代码的质量大有改善。
特别鸣谢出题目的老师和帮助我修改代码的同学们,让我有了提高自己的机会



 浙公网安备 33010602011771号
浙公网安备 33010602011771号