2025.01.20 练习

2-Coloring

2-着色

\(2.00\text{s}\)

\(250.00\text{MB}\)

题面翻译

输入正整数 \(n,m\)，要求把一个 \(n \times m\) 的棋盘染成蓝色和黄色，且每行恰好有一段蓝色的格子，每列恰好有一段黄色的格子。输出总方案数对 \(998244353\) 取模的结果。

\(n,m\le2021\)。

题目描述

有一个包含 $ n $ 行和 $ m $ 列的网格。网格中的每个单元格应该被涂成蓝色或黄色。

如果每一行恰好有一个蓝色单元格段，且每一列恰好有一个黄色单元格段，则称这种涂色为“愚蠢”的。换句话说，每行必须至少有一个蓝色单元格，并且每行中的所有蓝色单元格必须是连续的。类似地，每列必须至少有一个黄色单元格，并且每列中的所有黄色单元格也必须是连续的。

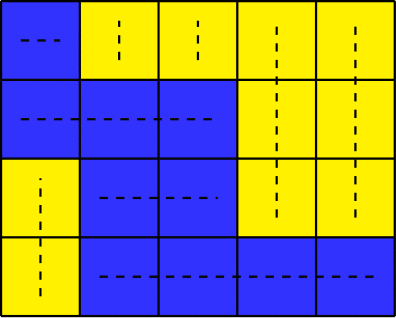一个愚蠢的涂色示例。 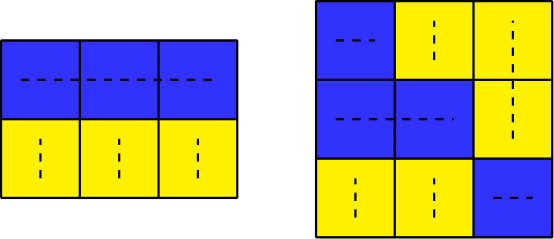聪明的涂色示例。第一个涂色在第二行缺少一个蓝色单元格，而第二个涂色在第二列有两个黄色段。请问网格中有多少种愚蠢的涂色？如果有某个单元格的颜色不同，则认为两种涂色是不同的。

输入格式

唯一一行包含两个整数 $ n $ , $ m $ ( $ 1\le n, m\le 2021 $ )。

输出格式

输出一个整数——愚蠢涂色的数量，取模 $ 998244353 $ 。

样例 #1

样例输入 #1

2 2

样例输出 #1

2

样例 #2

样例输入 #2

4 3

样例输出 #2

294

样例 #3

样例输入 #3

2020 2021

样例输出 #3

50657649

提示

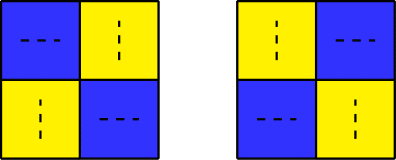
在第一组测试案例中，这些是唯一的两个愚蠢的 $ 2\times 2 $ 涂色。

[ARC169F] Large DP Table

大 DP 表

\(2.00\text{s}\)

\(1.00\text{GB}\)

题面翻译

给定长为 \(n\) 的数列 \(a_i,b_i,x_i,y_i\)，保证 \(a_1=1,b_1=2\) 且它们构成一组 \(\{1,\ldots,2n\}\) 的排列。定义数组 \(d_{i,j}\)，其中 \(d_{1,1}=0\)，若 \(a_i<b_j\)，则 \(d_{i,j}=d_{i,j-1}+x_i\)，否则 \(d_{i,j}=d_{i-1,j}+y_j\)，求 \(\sum_{i=1}^n\sum_{j=1}^n d_{i,j}\) 模 \(998244353\) 的结果。\(n\le 2.5\times 10^5\)。

题目描述

给定长度为 $ N $ 的整数列 $ A=(A_1,A_2,\cdots,A_N) $, $ B=(B_1,B_2,\cdots,B_N) $, $ X=(X_1,X_2,\cdots,X_N) $, $ Y=(Y_1,Y_2,\cdots,Y_N) \(。这里，\) A $ 和 $ B $ 满足以下性质：

• $ A_1=1 $
• $ B_1=2 $
• $ (A_1,A_2,\cdots,A_N,B_1,B_2,\cdots,B_N) $ 是 $ (1,2,\cdots,2N) $ 的一个排列。

定义整数 $ d_{i,j} $ ($ 1\ \leq\ i,j\ \leq\ N $ ) 如下：

• $ d_{1,1}=0 $
• 若 $(i,j)\ \neq\ (1,1) $ 且 $ A_i\ <\ B_j \(，则：\) d_{i,j}=d_{i,j-1}+X_i $
• 若 $(i,j)\ \neq\ (1,1) $ 且 $ A_i\ >\ B_j \(，则：\) d_{i,j}=d_{i-1,j}+Y_j $

求 $ \sum_{1\ \leq\ i\ \leq\ N}\sum_{1\ \leq\ j\ \leq\ N}d_{i,j} $ 对 $ 998244353 $ 的取模结果。

输入格式

输入以以下格式通过标准输入给出：

$ N $ $ A_1 $ $ A_2 $ $ \cdots $ $ A_N $ $ B_1 $ $ B_2 $ $ \cdots $ $ B_N $ $ X_1 $ $ X_2 $ $ \cdots $ $ X_N $ $ Y_1 $ $ Y_2 $ $ \cdots $ $ Y_N $

输出格式

输出答案。

样例 #1

样例输入 #1

2
1 4
2 3
2 2
1 3

样例输出 #1

8

样例 #2

样例输入 #2

3
1 3 5
2 6 4
1 10 100
1000 10000 100000

样例输出 #2

108153

样例 #3

样例输入 #3

3
1 6 5
2 4 3
1 10 100
1000 10000 100000

样例输出 #3

333009

样例 #4

样例输入 #4

10
1 17 4 7 16 18 9 3 12 6
2 19 20 14 5 11 13 8 15 10
744280520 249168130 239276621 320064892 910500852 164832983 245532751 198319687 715892722 967824729
769431650 80707350 459924868 257261830 777045524 583882654 950300099 438099970 322288793 532405020

样例输出 #4

746075419

提示

约束

• $ 2\ \leq\ N\ \leq\ 250000 $
• $ A_1=1 $
• $ B_1=2 $
• $ (A_1,A_2,\cdots,A_N,B_1,B_2,\cdots,B_N) $ 是 $ (1,2,\cdots,2N) $ 的一个排列。
• $ 1\ \leq\ X_i\ \leq\ 10^9 $
• $ 1\ \leq\ Y_i\ \leq\ 10^9 $
• 输入值均为整数。

样例解释 1

$ d_{i,j} $ 的值如下所示：

• $ d_{1,1}=0 $
• $ d_{1,2}=d_{1,1}+X_1=0+2=2 $
• $ d_{2,1}=d_{1,1}+Y_1=0+1=1 $
• $ d_{2,2}=d_{1,2}+Y_2=2+3=5 $

因此，要求的答案是 $ 0+2+1+5=8 $。