《算法》笔记 17 - 数据压缩

• 读写二进制数据
• 基因组数据的压缩
• 游程编码
  • 位图
• 霍夫曼压缩
  • 前缀码和单词查找树
  • 构造前缀码的单词查找树
  • 写入和读取单词查找树
  • 使用前缀码压缩
  • 使用前缀码展开
• LZW压缩
  • LZW的单词查找树
  • LZW的单词查找树
  • LZW压缩的展开

对数据进行压缩能够有效节省保存信息所需的空间和传输信息所需的时间。虽然计算机存储设备的成本在不断降低，但由于需要存储的数据在飞速膨胀，压缩算法仍有非常重要的意义，因为与以往相比，数据被压缩后节省的空间会更大。

读写二进制数据

现代计算机系统中处理的所有类型的数据最终都是用二进制表示的，可以将它们都看作一串比特的序列。

数据压缩分为无损压缩和有损压缩，前者在压缩、展开后不会丢失任何信息，但后者不然。有损压缩常被用于图像、视频、音乐的压缩。对于无损压缩算法，评价的标准为压缩率，压缩率=压缩后体积/原始体积；对于有损压缩算法，评价标准除了压缩率外，还有主观的质量感受等。
接下来只讨论无损压缩算法。

之前的算法设计输入输出时，使用的都是基于java基础方法封装的StdIn和StdOut，它们处理的是由Unicode编码的字符流；但由于压缩算法会涉及到对比特流的操作，所以接下来使用BinaryStdIn和BinaryStdOut，BinaryStdIn.readBoolean()方法会从输入中读取一个比特并返回为布尔值，BinaryStdOut.write(boolean b)方法则会向输出中写入一个比特。

基因组数据的压缩

接下来从初级的基因组压缩算法开始，因为表示基因组的字符集只含有A C T G四个字符。这种方法也适用于字符集大小固定且数量有限的场合。
如果将这四个字符直接用ASCII编码，需要4×8=32位，但其实只需要用两个位就可以表示4个值（2^2=4）。这样4个字符只需要2×4=8位就可以了，压缩率=8/32=25%。
由此可得对基因组数据的压缩方法：

public static void compress(){
    Alphabet DNA=new Alphabet("ACTG");
    String s=BinaryStdIn.readString();
    int N=s.length();
    BinaryStdOut.write(N);
    
    for(int i=0;i<N;i++){
        int d=DNA.toIndex(s.charAt(i));
        BinaryStdOut.write(d,DNA.lgR());
    }
    BinaryStdOut.close();
}

实例化Alphabet类时，指定字符集只有ACTG这四个，DNA.lgR()就等于2，每次输出2个比特。比如遇到字符A，就用0表示，二进制编码为00，字符B用1表示，二进制编码为01等等。

展开时，每次读取2个比特，转换为整型数字，然后根据这个数字去字符集中取得对应的字符。

public static void expand(){
    Alphabet DNA=new Alphabet("ACTG");
    int w=DNA.lgR();
    int N=BinaryStdIn.readInt();
    for(int i=0;i<N;i++){
        char c=BinaryStdIn.readChar(w);
        StdOut.println("c="+c);
        char e=DNA.toChar(c);
        StdOut.println("e="+e);
        BinaryStdOut.write(DNA.toChar(c));
    }
    BinaryStdOut.close();
}

游程编码

比特流中最简单的冗余形式就是一长串重复的比特，游程编码就是利用这种冗余来压缩数据的经典方法，在对位图的压缩中有很好的效果。

位图

位图经常用于保存图像和扫描文档，下面是一张最简单的位图，分辨率为32×48，图像为一个“q”字符，用按行排列的比特流来表示位图数据，所以这张简单的位图是没有颜色信息的，或者说只有两种颜色。

00000000000000000000000000000000
00000000000000000000000000000000
00000000000000011111110000000000
00000000000011111111111111100000
00000000001111000011111111100000
00000000111100000000011111100000
00000001110000000000001111100000
00000011110000000000001111100000
00000111100000000000001111100000
00001111000000000000001111100000
00001111000000000000001111100000
00011110000000000000001111100000
00011110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111111000000000000001111100000
00111111000000000000001111100000
00011111100000000000001111100000
00011111100000000000001111100000
00001111110000000000001111100000
00001111111000000000001111100000
00000111111100000000001111100000
00000011111111000000011111100000
00000001111111111111111111100000
00000000011111111111001111100000
00000000000011111000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000011111110000
00000000000000000011111111111100
00000000000000000111111111111110
00000000000000000000000000000000
00000000000000000000000000000000

取这个位图中的第5行来分析

00000000001111000011111111100000

这条长度32的字符串中，含有：10个0 - 4个1 - 4个0 - 9个1 - 5个0。所有的比特字符串都是类似这样，0和1交替出现，所以对于这条字符串，就可以编码为10，4，4，9，5，如果用4比特表示长度，并以连续的0作为开头，就可以得到一个20位长的字符串（不包含逗号）：1010,0100,0100,1001,0101。压缩率=20/32=62.5%。

4位编码能表示的值只有0到15，在实际的应用中是不够的，所以使用8位编码，可以表示0-255之间的游程长度。如果游程的长度超过256，就插入一个长度为0的游程，这样可以确保所有的游程长度都不超过256。

使用游程编码压缩的代码如下：

public static void compress() {
    char cnt = 0;
    boolean b, old = false;
    while (!BinaryStdIn.isEmpty()) {
        b = BinaryStdIn.readBoolean();
        if (b != old) {
            BinaryStdOut.write(cnt);
            cnt = 0;
            old = !old;
        } else {
            if (cnt == 255) {
                BinaryStdOut.write(cnt);
                cnt = 0;
                BinaryStdOut.write(cnt);
            }
        }
        cnt++;
    }
    BinaryStdOut.write(cnt);
    BinaryStdOut.close();
}

算法会逐个读取比特位，如果它和上一个比特相同，就把游程计数器cnt加1；如果计数器已满，就将其输出为编码，然后计数器归零，并输出一个长度为0的游程来分割过长的相同编码；如果它和上一个比特不同，就将计数器的值输出然后归零。

展开的代码为：

public static void expand() {
    boolean b = false;
    while (!BinaryStdIn.isEmpty()) {
        char cnt = BinaryStdIn.readChar();
        for (int i = 0; i < cnt; i++)
            BinaryStdOut.write(b);
        b = !b;
    }
    BinaryStdOut.close();
}

展开时每次读取一个游程的长度（8位编码），先输出比特0，按照游程指定的长度输出完毕后，切换状态，继续输出。

游程编码被广泛用于位图的压缩，这种压缩方式还有一项特殊的优势在于，随着位图分辨率的提高，它的效果也会大大提高。如果位图分辨率增加一倍，它的总比特数将变为原来的4倍，但游程的数量只会变为原来的2倍，因为横向的比特数增加不会影响游程的数量，只会影响游程的长度，这样压缩后的比特数量变为约原来的2倍，所以压缩率减半。
但游程编码只在游程较长时效果较好，如果游程很短，这种算法可能反而会增加比特数。

霍夫曼压缩

前缀码和单词查找树

虽然游程编码在许多场景非常有效，但有的时候需要压缩的数据特征并不具有较长的游程，比如英文文档等自然语言文件，霍夫曼压缩算法和LZW压缩算法对这种特征的数据也能取得很好的效果。
霍夫曼压缩的主要思想是，放弃文本文件的普通保存方式，不再使用7位或8位二进制数表示一个字符，而是用较少的比特表示出现频率高的字符，用较多的比特表示出现频率低的字符。
比如对于字符串 A B R A C A D A B R A，如果使用7位的ASCII字符编码，那么只出现了1次的D和出现了5次的A，占用的比特数是一样的。
如果能这样编码

A:0
B:1
R:00
C:01
D:10

那么这个字符串的编码就是0 1 00 0 01 0 10 0 1 00 0。只需要15位，而ASCII码需要77位。但这种方法并不完整，因为它需要空格来区分字符，如果没有空格，就会造成歧义，比如01，除了可以解码为AB，还可以解码为C。
如果能够让所有字符编码都不会成为其他字符编码的前缀，就不需要专门的分隔符了。含有这种性质的编码规则叫做前缀码。
前缀码的一种简便表示方法就是单词查找树。

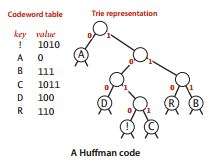
如图所示的单词查找树，就是一种字符的编码方式，它的左链接表示0，右链接表示1，每个字符的编码就是从根结点到该结点的路径表示的比特字符串。
不同的单词查找树表示的前缀码的压缩率不相同，霍夫曼压缩算法构造的单词查找树是最优的。

霍夫曼压缩分为5个步骤：

• 压缩时：
  • 构造前缀码的单词查找树
  • 将树以字节流的形式输出
  • 使用构造的树将字节流编码为比特流
• 展开时：
  • 读取单词查找树
  • 使用该树将比特流解码

构造前缀码的单词查找树

单词查找树的结点

public static class Node implements Comparable<Node> {
    private char ch;
    private int freq;
    private final Node left, right;

    Node(char ch, int freq, Node left, Node right) {
        this.ch = ch;
        this.freq = freq;
        this.left = left;
        this.right = right;
    }

    public boolean isLeaf() {
        return left == null && right == null;
    }

    public int compareTo(Node that) {
        return this.freq - that.freq;
    }
}

这份树结点的实现中，除了用于表示左右结点的left、right和表示叶子节点中字符的ch，还增加了一个整型变量freq，用于统计字符出现的频率。

构造单词查找树

霍夫曼算法是一个两轮算法,为了构造单词查找树，算法会先读取一次整个输入流，得到每个字符的频率。
构造的第一步是创建一片由许多只有一个结点的树所组成的森林，每棵树都表示输入流中的一个字符。然后自底向上根据频率构造单词查找树，找到两个频率最小的结点，创建一个包含着两个子结点的新结点，新结点的频率值为两个子结点的频率值之和，不断重复这个过程，直到所有子树都合并为一颗树。

private static Node buildTrie(int[] freq) {
    MinPQ<Node> pq = new MinPQ<Node>();
    for (char c = 0; c < R; c++)
        if (freq[c] > 0)
            pq.insert(new Node(c, freq[c], null, null));
    while (pq.size() > 1) {
        Node x = pq.delMin();
        Node y = pq.delMin();
        Node parent = new Node('\0', x.freq + y.freq, x, y);
        pq.insert(parent);
    }
    return pq.delMin();
}

用最小优先队列可以方便快速的找到最小结点。

写入和读取单词查找树

写入

霍夫曼压缩算法需要在压缩时将树写入比特流并在展开时读取它。写入时，对单词查找树进行前序遍历，遇到内部结点时，写入比特0，遇到叶子结点时，写入比特1，紧接着是这个结点中字符的8为ASCII码。

private static void writeTrie(Node x) {
    if (x.isLeaf()) {
        BinaryStdOut.write(true);
        BinaryStdOut.write(x.ch);
        return;
    }
    BinaryStdOut.write(false);
    writeTrie(x.left);
    writeTrie(x.right);
}

读取

在读取比特字符串，重新构造单词查找树时，首先读取一个比特以确定当前结点的类型，如果是叶子结点，就读取字符并创建一个叶子节点，如果是内部结点，就创建一个内部结点并递归地构造它的左右子树。

private static Node readTrie() {
    if (BinaryStdIn.readBoolean())
        return new Node(BinaryStdIn.readChar(), 0, null, null);
    return new Node('\0', 0, readTrie(), readTrie());
}

使用前缀码压缩

在压缩时，首先根据单词查找树定义的前缀码来构造编译表。为了提升效率，使用由字符索引的数组st，st的大小为字符集的大小。st中保存了单词查找树中包含的字符对应的比特字符串。
在构造编译表时，会递归遍历整颗树，并为每个结点维护了一条从跟结点到它的路径所对应的二进制字符串，0表示左链接，1表示右链接，每当到达一个叶子节点时，就将结点的编码设为它对应的比特字符串。

private static void buildCode(String[] st, Node x, String s) {
    if (x.isLeaf()) {
        st[x.ch] = s;
        return;
    }
    buildCode(st, x.left, s + '0');
    buildCode(st, x.right, s + '1');
}

编译表建立后，压缩的过程，就成了查找树如字符所对应的编码并写入的过程。

public static void compress() {
    String s = BinaryStdIn.readString();
    char[] input = s.toCharArray();

    int[] freq = new int[R];
    for (int i = 0; i < input.length; i++)
        freq[input[i]]++;

    Node root = buildTrie(freq);
    String[] st = new String[R];
    buildCode(st, root, "");
    writeTrie(root);
    BinaryStdOut.write(input.length);
    for (int i = 0; i < input.length; i++) {
        String code = st[input[i]];
        for (int j = 0; j < code.length(); j++)
            if (code.charAt(j) == '1')
                BinaryStdOut.write(true);
            else
                BinaryStdOut.write(false);
    }
    BinaryStdOut.close();
}

使用前缀码展开

在展开时，首先使用前述方法从比特流中还原单词查找树。然后根据比特流的输入从跟结点开始向下移动，如果比特为0，就移动到左子结点，反之就移动到右子结点。当遇到叶子结点时，输出这个结点的字符并重新回到根结点。

public static void expand() {
    Node root = readTrie();
    int N = BinaryStdIn.readInt();
    for (int i = 0; i < N; i++) {
        Node x = root;
        while (!x.isLeaf())
            if (BinaryStdIn.readBoolean())
                x = x.right;
            else
                x = x.left;
        BinaryStdOut.write(x.ch);
    }
    BinaryStdOut.close();
}

LZW压缩

LZW算法的基本思想和霍夫曼压缩的思想正好相反。霍夫曼压缩是为输入中的定长模式产生了变长的编码编译表；而LZW压缩是为输入中的变长模式生成了一张定长的编码编译表。而且，LZW算法不需要在输出中附上这张编译表。

LZW压缩算法的基础是维护一张字符串键和编码的编译表。在符号表中，将128个ASCII码的值初始化为8位编码，即在每个字符的编码值前面添加0。然后用16进制数字来表示编码，那么A的编码就是41，R的是52等等。将80编码保留为文件借宿的标志，并将81-FF的编码值分配给在输入中遇到的各种子字符串。
压缩数据时，会反复进行如下操作：

• 找出未处理的输入在符号表中最长的前缀字符串s；
• 输出s的8位编码值；
• 继续扫描s之后的一个字符c；
• 在符号表中将s+c（连接s和c）的值设为下一个编码值。

比如下图所示为处理输入A B R A C ... B R A的过程，以及对应的三向单词查找树：

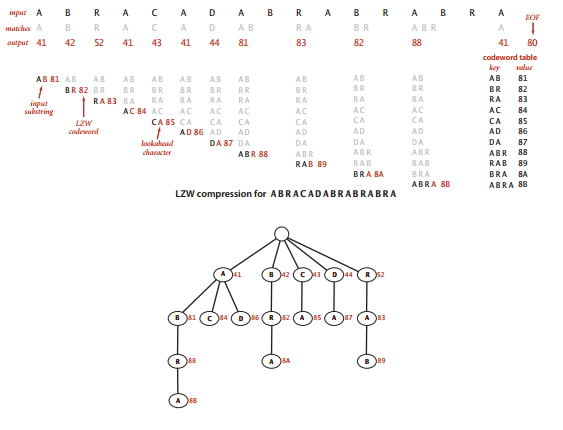
对于前7个字符，匹配的最长前缀只有1个字符，因此输出这些字符对应的编码，并将编码81到87和产生的7个双字符的字符串关联。然后发现AB匹配了输入的前最81，并将ABR添加到符号表中，然后是RA（输出83并添加RAB），BR（输出82并添加BRA）和ABR（输出88并添加ABRA），最后只剩下A（输出41）。

LZW的单词查找树

LZW算法会用到三向单词查找树，包含两种操作：

• 找到输入和符号表的所有键的最长前缀匹配；
• 将匹配的键和前瞻字符相连得到一个新键，将新键和下一个编码管理并添加到符号表中。

LZW压缩的展开

在展开时，会维护一张关联字符串和编码值的符号表，这张表的逆表示压缩时所用的符号表。在这张表总加入00到7F和所有单个ASCII字符的字符串的关联条目，将第一个未关联的编码值设为81。在遇到编码80前，不断重复以下操作：

• 输出当前字符串val；
• 从输入中读取一个编码x；
• 在符号表中将s设为和x相关联的值；
• 在符号表中将下一个未分配的编码值设为val+c，其中c为s的首字母；
• 将当前字符串val设为s；

最终LZW算法的实现如下，这份用于实际使用的代码，采用的编码宽度为12位。

public class LZW {
    private static final int R = 256;
    private static final int L = 4096;
    private static final int W = 12;

    public static void compress() {
        String input = BinaryStdIn.readString();
        TST<Integer> st = new TST<Integer>();

        for (int i = 0; i < R; i++)
            st.put("" + (char) i, i);
        int code = R + 1;

        while (input.length() > 0) {
            String s = st.longestPrefixOf(input);
            BinaryStdOut.write(st.get(s), W);

            int t = s.length();
            if (t < input.length() && code < L)
                st.put(input.substring(0, t + 1), code++);
            input = input.substring(t);
        }

        BinaryStdOut.write(R, W);
        BinaryStdOut.close();
    }

    public static void expand() {
        String[] st = new String[L];
        int i;
        for (i = 0; i < R; i++)
            st[i] = "" + (char) i;
        st[i++] = " ";

        int codeword = BinaryStdIn.readInt(W);
        String val = st[codeword];
        while (true) {
            BinaryStdOut.write(val);
            codeword = BinaryStdIn.readInt(W);
            if (codeword == R)
                break;
            String s = st[codeword];
            if (i == codeword)
                s = val + val.charAt(0);
            if (i < L)
                st[i++] = val + s.charAt(0);
            val = s;
        }
        BinaryStdOut.close();
    }
}