《算法》笔记 8 - 二叉查找树
- 二叉查找树
- 查找
- 插入
- 性能
- 有序性相关的操作
- 最大键、最小键
- 向上取整、向下取整
- 选择、排名
- 范围查找
- 删除操作
- 删除最大键、最小键
- 通用删除操作
二叉查找树
前面了解的无序链表和有序数组在性能方面至少在线性级别,无法用于数据量大的场合。接下来要学习的二叉查找树可以将链表插入的灵活性和有序数组查找的高效性结合起来,是计算机科学中最重要的算法之一。
一个二叉查找树(Binary Search Tree)是一颗二叉树,其中每个结点都含有一个Comparable的键,以及相关联的值,且每个结点的键都大于其左子树中任意结点的键,小于右子树中任意结点的键。
查找
在二叉查找树中查找时,如果树是空的,则查找未命中;如果被查找的键和根结点的键相等,查找命中,否则就递归地在子树中继续查找,如果被查找的键小于根结点,就选择左子树,否则选择右子树。
查找算法的代码实现为:
public class BST<Key extends Comparable<Key>, Value> {
private Node root;
private class Node {
private Key key;
private Value val;
private Node left, right;
public int size;
public Node(Key key, Value val, int size) {
this.key = key;
this.val = val;
this.size = size;
}
}
public Value get(Key key) {
return get(root, key);
}
private Value get(Node x, Key key) {
if (key == null)
throw new IllegalArgumentException("calls get() with a null key");
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp > 0) {
return get(x.right, key);
} else if (cmp < 0) {
return get(x.left, key);
} else {
return x.val;
}
}
}
其中,Node类用来表示二叉查找树的结点,每个结点都含有键、值、左右链接和一个后面实现最大最小值等有序操作时会用到的结点计数器。
插入
插入键值对时,首先进行查找,如果键已经存在于符号表中,则更新对应的值;如果查找未命中,就返回一个含有待插入键值对的新结点。
public void put(Key key, Value val) {
root = put(root, key, val);
}
private Node put(Node x, Key key, Value val) {
if (key == null)
throw new IllegalArgumentException("calls put() with a null key");
if (x == null)
return new Node(key, val, 1);
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = put(x.left, key, val);
else if (cmp > 0)
x.right = put(x.right, key, val);
else {
x.val = val;
}
x.size = size(x.left) + size(x.right) + 1;
return x;
}
插入操作的代码与查找类似,但插入操作会更新结点值或添加新结点,并且会更新结点计数器。
x.left = put(x.left, key, val); 类似这样的代码利用递归的特性简洁地实现了结点的添加。在递归调用时,相当于根据二分查找的逻辑,沿着树的某个分支一直向下查找,如果找到,就终止递归,更新结点的值,如果到了树的最底层也没找到,此时key==null成立,递归也会终止,同时新初始化的结点也已经被挂在x.left或者x.right了。
在递归推出的过程中,相当于沿着树向上爬,每爬一层,x.size = size(x.left) + size(x.right) + 1;都会被执行,这样在添加结点后,相关路径上的所有结点的size都得到了更新。
性能
插入新结点和未命中的查找都需要从整颗树的根结点搜索到树的最底层,所以二叉查找树的性能与树的形状有关,因为树的形状决定了树的深度。在最好的情况下,一个含有N个结点的树是完全平衡的,所有的空链接都在最底层,距离根结点的距离为LgN;而在最坏的情况下,树的形状变成了一条链表,树的深度为N,将元素按顺序逐个插入到二叉查找树时,就可以造成这种情况。在一般的情况下,得到的树的形状与最好情况更加接近,二叉查找树的性能在对数级别。
英文原版《双城记》中大于7个字符的单词一共14350个,这些单词中不同的单词有5737个,将这些单词作为键来测试不同符号表实现的性能,结果如下:
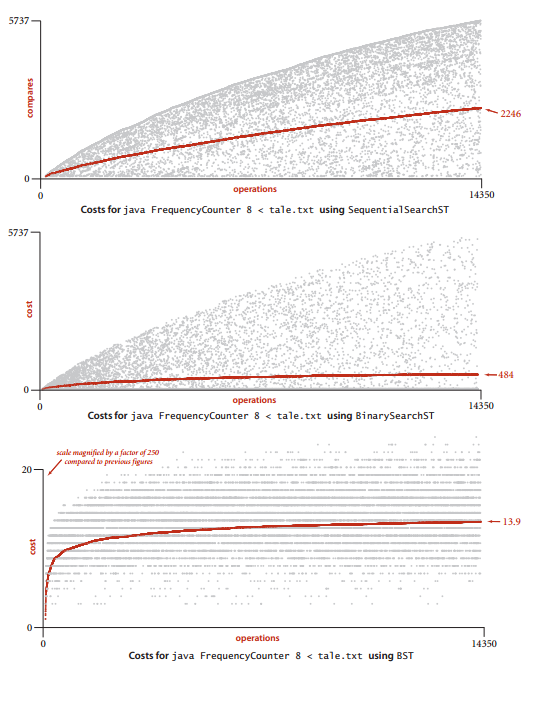
图中横坐标表示插入单词的数量,纵坐标表示插入时的比较次数,灰点表示某次插入的实际比较次数,红点表示平均比较次数(比较总数/插入单词数量),前面学习过基于无序链表和有序数组的实现,平均次数分别为2246和484次,可以看到二叉查找树无论在单词比较次数还是平均次数方面,都有了跨越数量级的进步。
有序性相关的操作
二叉查找树除了拥有较好的性能,还因其能够保持键的有序性而支持有序性相关的操作。
最大键、最小键
一个结点的左子树的值都小于右子树,所以最小值可能在左子树中,如果左子树为空,则当前结点就是最小值。基于这种算法得出求最大值、最小值的代码实现为:
public Key min() {
if (isEmpty())
throw new NoSuchElementException("calls min() with empty symbol table");
return min(root).key;
}
private Node min(Node x) {
if (x.left == null)
return x;
else
return min(x.left);
}
public Key max() {
if (isEmpty())
throw new NoSuchElementException("calls max() with empty symbol table");
return max(root).key;
}
private Node max(Node x) {
if (x.right == null)
return x;
else
return max(x.right);
}
向上取整、向下取整
关于向下取整,如果给定键小于根结点的键,那么小于等于给的键的最大值在根结点的左子树中,如果给定的键大于根结点,那么只有当根结点右子树中存在小于等于给定键的结点时,向下取整的值会出现在右子树中,否则根结点就是要找的值,向上取整的方法与此类似:
public Key floor(Key key) {
Node n = floor(root, key);
if (n == null) {
return null;
} else {
return n.key;
}
}
private Node floor(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0)
return x;
if (cmp < 0)
return floor(x.left, key);
Node n = floor(x.right, key);
if (n == null) {
return x;
} else {
return n;
}
}
public Key ceiling(Key key) {
if (n == null) {
return null;
} else {
return n.key;
}
}
private Node ceiling(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0)
return x;
if (cmp > 0)
return ceiling(x.right, key);
Node n = ceiling(x.left, key);
if (n == null) {
return x;
} else {
return n;
}
}
选择、排名
排名从0开始,选择方法select(k)会返回排名为的键,树中有k个小于它的键。如果左子树中的结点数t大于k,就继续在左子树中查找,如果t等于k,那么根结点就是要找的键,如果t小于k,就在右子树中查找排名为k-t-1的键,由此得到的代码为:
public Key select(int k) {
return select(root, k).key;
}
private Node select(Node x, int k) {
if (x == null) {
return null;
}
int t = size(x.left);
if (t > k) {
return select(x.left, k);
} else if (t < k) {
return select(x.right, k - t - 1);
} else {
return x;
}
}
排名rank()方法是选择方法的逆方法,它返回给定键的排序。如果给定键与根结点相等,那么键的排名就是根结点左子树中的结点总数t;如果给定键小于根结点,在左子树中继续递归计算;如果给定键大于根结点,就返回t+1再加上它在右子树中的排名。
public int rank(Key key) {
return rank(key, root);
}
private int rank(Key key, Node x) {
if (x == null) {
return 0;
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
return size(x.left) + rank(key, x.right) + 1;
} else if (cmp < 0) {
return rank(key, x.left);
} else {
return size(x.left);
}
}
范围查找
范围查找要求返回给定范围内的所有键,这里会用到遍历二叉树的基本方法-中序遍历。先遍历左子树中的所有键,然后遍历根结点,最后是右子树中的所有键,这一过程递归地进行,就可以按从小到大的顺序遍历完所有结点。
public void keys(Node x, Queue<Key> queue, Key lo, Key hi) {
if (x == null)
return;
int cmplo = lo.compareTo(x.key);
int cmphi = hi.compareTo(x.key);
if (cmplo < 0)
keys(x.left, queue, lo, hi);
if (cmplo <= 0 && cmphi >= 0)
queue.enqueue(x.key);
if (cmphi > 0)
keys(x.right, queue, lo, hi);
}
删除操作
删除最大键、最小键
删除最小键时,需要不断地深入根结点的左子树,直到遇见一个空链接,然后将指向该结点的链接指向该结点的右子树,要被删除的结点因为没有被任何对象引用,随后就会被垃圾回收器清理掉。删除最大键的过程类似。
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node x) {
if (x.left == null)
return x.right;
x.left = deleteMin(x.left);
x.size = size(x.left) + size(x.right) + 1;
return x;
}
public void deleteMax() {
root = deleteMax(root);
}
private Node deleteMax(Node x) {
if (x.right == null)
return x.left;
x.right = deleteMax(x.right);
x.size = size(x.left) + size(x.right) + 1;
return x;
}
在不断深入左子树的时候,除非遇见空链接,deleteMin(Node x)方法都返回结点x,只有最后一次递归才将上个结点指向x.right,递归退出时,会更新路径上的结点计数器。
通用删除操作
二叉查找树中最难实现的方法就是delete()方法了,删除最大、最小键时,被删除的结点的两个子结点中,只有一个不为空,但一般的结点都会有两个子结点,删除这个结点后,需要合理处理它的两个子结点。T.Hibbard在1962年提出了解决这个难题的第一个方法,在删除结点x后用它的后继结点填补它的位置。因为x有一个右子结点,由此它的后继结点就是其右子树中的最小结点。这样的替换仍然能保证树的有序性,因为x.key和它的后继结点之间不存在其他的键。完成这个操作需要4步:
- 将指向即将被删除的结点的链接保存为t;
- 将x指向它的后继结点min(t.right);
- 将x的右链接(原本指向一颗所有结点都大于x.key的二叉查找树)指向deleteMin(t.right),也就是在删除后所有结点仍然后大于x.key的子二叉查找树。
- 将x的左链接(原本为空)设为t.left(其下所有的键都小于被删除的结点和它的后继结点)。
public void delete(Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = delete(x.left, key);
else if (cmp > 0)
x.right = delete(x.right, key);
else {
if (x.right == null)
return x.left;
if (x.left == null)
return x.right;
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.size = size(x.left) + size(x.right) + 1;
return x;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号