因数个数函数与因数和函数

因数个数函数与因数和函数

$d(n)$表示n的因数的个数函数。$\sigma(n)$表示n的所有因数的和的函数。

积性

这两个函数都是积性函数。即$gcd(a,b)=1 \Rightarrow f(ab)=f(a)f(b)$.

因数个数函数$d(n)$积性证明思路

对于因数个数函数$d(n)$只需要用质因数分解的唯一性公式对进行质因数分解，利用简单的组合数学的知识可以知道$d(n)$的数学表达式。
当$gcd(a,b)=1$时，说明$a$与$b$分解质因数后没有公共的素因子。将$d(ab),d(a),d(b)$分解用数学表达式表达出来容易证明$d(ab)=d(a)d(b)$.

因数和函数$\sigma(n)$积性证明思路

这个稍微复杂一丢丢。
$gcd(a,b)=1$,即它们互质。
通过分解质因数的方法，容易说明：

1. $a,b$集合各取一个因数，它们的乘积一定是$ab$的因数。
2. 容易证明$ab$的因数一定可以分解为两个数的积，一个是$a$的因数，一个是$b$的因数。
   所以$a,b$各取一个因数$a_i,b_j$,就可以构造一个$ab$的因数$a_ia_j$.上面两点可以保证了我们不会漏取。
   所以，剩下的工作就是说明不会重复即可。
   也就是要说明$a_{i_1}b_{j_1}=a_{i_2}b_{j_2}$成立当且仅当$i_1=i_2\text{且}j_1=j_2$。
   这个只需要利用$a,b$互质，有$gcd(a_i,b_j)=1$。
   然后由$gcd(a_{i_1},b_{j_2})=1$，得到$b_{j_2} \mid b_{j_1}$.
   同理$gcd(a_{i_2},b_{j_1})=1$，可以得到$b_{j_1} \mid b_{j_2}$.于是就迅速得到$j_1=j_2$.
   同理就可以得到$i_1=i_2$.
   这就说明不可能重复了。于是$\sigma(ab)=\sum\limits_{i=1}^{d(a)}\sum\limits_{j=1}^{d(b)}\left(a_ib_j\right)$
   之后只需要用求和符号求和化简即可得到符合积性的结论。
   $\sigma(ab)=\sum\limits_{i=1}^{d(a)}\sum\limits_{j=1}^{d(b)}\left(a_ib_j\right)=\sum\limits_{i=1}^{d(a)}\left(a_i\sum\limits_{j=1}^{d(b)}b_j\right)=\sum\limits_{i=1}^{d(a)}\left(a_i\sigma(b)\right)=\sigma(b)\sum\limits_{i=1}^{d(a)}\left(a_i\right)=\sigma(a)\sigma(b)$

说说这两个函数程序如何求值

对于个数函数，显然是分解质因数，获取各个素因子的指数，然后用那个数学表达式算了。
对于因数和函数，如果规模比较小，图方便的话，自然是暴力枚举，试除相加即可。
规模稍微大一点，就利用积性了，分成互质的数的乘积，然后分别算每一部分的因数和，最后相乘即可。
如何保证互质，分解质因数后的那个表达式，每个素因子连同指数当作一个数，不就两两互质了，而且$\sigma(p^k)$的还是一个等比数列求和.

$d(n)$的一个性质——$d(n)=\sum\limits_{x \mid a}\sum\limits_{y|b}\left[gcd(x,y)=1\right]$

假设我们$n=ab$，不要求$a,b$互质。
那么有$d(n)=\sum\limits_{x \mid a}\sum\limits_{y|b}\left[gcd(x,y)=1\right]$.

怎么理解

即将$n$分解成$n=ab$，然后找有序对$(x,y)$，$x,y$分别是$a,b$的因数，并且限制$x,y$互质。

为什么等号成立？

分解质因数，组合数学就知道了。
对于一个数来说，要构造一个因数，就是对分解质因数后的每个质因子选一个指数，有多少种选法就有多少个因数。
不同质因数选指数是独立的，适用乘法原理；对一个固定的质因子$p$，假设分解质因数形式里的指数是$k$,则构造因数时选取指数的范围是从$0$到$k$共$k+1$种。
现在我们将$n$分成$a,b$分成两部分了，
下面是个示意图，每个各自代表一个质数，红色的是$a$和$b$共有的质因子。绿色的是a含有而b不含有的素因子，蓝色的是b含有而a不含有的素因子。
我们给素因子选一个指数的时候就是往代表这个素因子的格子里填一个指数。
只是我们现在不是直接往$n$分解之后的格子里填数。而是先分别对$a，b$的分解后的格子里填数构造因数$x,y$.

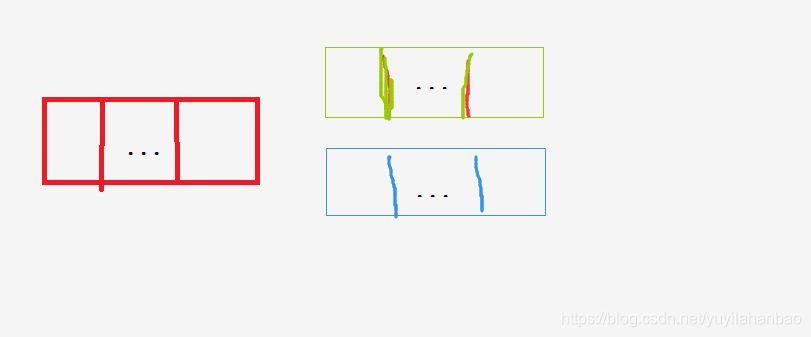
对于红色格子，我们限定$a,b$填数的时候不能同时往同一个格子里填数。即对于同一个红色格子，那么只有以下可能：

1. a和b都没有选，即都填了0
2. a选了，填的是$1,2,\ldots,k_a$中的一个；b没选，即填了0
3. b没选，填了0；a没选，b选了，$1,2,\ldots,k_b$中的一个
   于是$a,b$和b分开填对于这个红色格子，一共有$1+k_a+k_b$种可能。
   而$n=ab$直接分解往里面填数字的时候，对于这个红色格子，能填的范围刚好是$0,1,2,3,\ldots,k_a+k_b$共$1+k_a+k_b$种可能。
   显然，做了不能往同一个格子里填数的限制之后，所有方案是一样的，如果不做这个限制，就不能保证一样了。
   对于绿色格子和蓝色格子，由于是各自独有的，显然$a,b$分别填和$n$直接分解填的方案数是一样的。
   所以最终方案数是一样的。

所以，我们只需要$a$和$b$分别填指数构造自己的因数$x,y$，统计填法的方案数即可，只是要保证不能对同一个素因子都填非零的指数即可。
那么怎么保证？那么怎么保证？那么怎么保证？
如果他们选用了相同的素因子$p$，显然$a$构造出的因数$x$和$y$构造的因数就含有公约数$p$，所以只需要保证$x,y$互质即可。