26年佛山一模第19题 圆锥曲线定点定值问题

专题：圆锥曲线 \(\qquad \qquad \qquad \qquad\) 题型：定点定值问题 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★★★

经典例题讲解尽量从学生的角度出发，重在引导思考与总结!

【题目】

(26年佛山一模第19题)
已知点\(A(2，3)\)，\(B(2，1)\)，双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2} =1(a>0，b>0)\)的一条渐近线方程是\(y=x\)，直线\(AB\)被\(C\)截得的弦长为\(2\sqrt{3}\).
(1) 求\(C\)的方程；
(2) 已知\(P\)，\(Q\)是\(C\)的右支上不同的两点，且存在实数\(λ\)，使得\(\overrightarrow{AP}=λ\overrightarrow{AQ}\).
    (i) 若点\(D\)满足\(\overrightarrow{PD}=λ\overrightarrow{DQ}\)，求证：点\(D\)总在某定直线上.
    (ii) 若直线\(PB\)与\(C\)的另一个交点为\(R\)(异于\(Q\))，求证：直线\(QR\)过定点，并求出该定点的坐标.

 
 
 
 
 
 

【解答】

第一问

\(∵\)一条渐近线为\(y=x\)，\(∴a=b\)①，
\(∵\)直线\(AB\)被\(C\)截得的弦长为\(2\sqrt{3}\)，\(∴\)点\((2，\sqrt{3})\)在双曲线上，
\(∴\dfrac{4}{a^2}-\dfrac{3}{b^2} =1\)②，
由①②解得\(a=b=1\)，
所以\(C\)的方程为\(x^2-y^2=1\)；
 

第二问第1小问

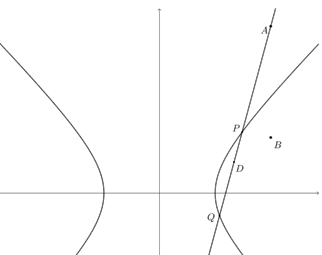
方法1

思路：要证明点\(D\)总在某定直线上，可尝试求出动点\(D(x_0，y_0)\)的轨迹方程，即得到关于\(x_0，y_0\)的等式.
设点\(P(x_1，y_1)\)，\(Q(x_2，y_2)\)，\(D(x_0，y_0)\)，
设直线\(PQ\)的方程为\(x=m(y-3)+2\)，
(设为横截式比点斜式会更好，避免分离讨论)
联立\(x^2-y^2=1\)，得\((m^2-1) y^2+(4m-6m^2 )y+9m^2-12m+3=0\)，
(严格来说，要根据\(∆>0\)求出\(m\)的取值范围，但该问并不是真的求动点\(D\)的轨迹方程，而只需要是否在一直线上，故不求出\(m\)的取值范围也可以)
\(∴y_1+y_2=\dfrac{6m^2-4m}{m^2-1}\)，\(y_1 y_2=\dfrac{9m^2-12m+3}{m^2-1}\)，
\(∵\overrightarrow{AP}=λ\overrightarrow{AQ}\)，\(\overrightarrow{PD}=λ\overrightarrow{DQ}\)，
\(∴(x_1-2，y_1-3)=λ(x_2-2，y_2-3)\)，\((x_0-x_1，y_0-y_1 )=λ(x_0-x_2，y_0-y_2 )\)，
(遇到向量关系，利用坐标表示是最直接简洁的想法)
\(∴λ=\dfrac{y_1-3}{y_2-3}\)，\(λ=\dfrac{y_0-y_1}{y_0-y_2}\)，
\(∴y_0=\dfrac{y_1+λy_2}{1+λ}=\dfrac{y_1+y_2\cdot \dfrac{y_1-3}{y_2-3}}{1+\dfrac{y_1-3}{y_2-3}}=\dfrac{2y_1 y_2-3(y_1+y_2)}{y_1+y_2-6}\)\(=\dfrac{2\cdot \dfrac{9m^2-12m+3}{m^2-1}-3\cdot \dfrac{6m^2-4m}{m^2-1}}{\dfrac{6m^2-4m}{m^2-1}-6}=\dfrac{6-12m}{6-4m}=3+\dfrac{6}{2m-3}\)，
(分离常数法，为后面消参作准备)
又\(∵x_0=m(y_0-3)+2=5+\dfrac{9}{2m-3}\)，
(其实得到了动点\(D\)的参数方程\(\left\{ \begin{array}{c} x_0=5+\dfrac{9}{2m-3}\\ y_0=3+\dfrac{6}{2m-3} \end{array} \right. \)，消参\(m\)便可得到轨迹方程)
\(∴\dfrac{x_0-5}{9}=\dfrac{y_0-3}{6}\)，即\(2x_0-3y_0-1=0\)，
\(∴\)点\(D\)总在定直线\(2x-3y-1=0\)上；
 

方法2

来自其他老师解法

设点\(P(x_1，y_1)\)，\(Q(x_2，y_2)\)，\(D(x_0，y_0)\)，
\(∵\overrightarrow{AP}=λ\overrightarrow{AQ}\)，\(∴\overrightarrow{PA}= -λ\overrightarrow{AQ}\)，

\(∴\left\{ \begin{array}{c} 2=\dfrac{x_1-λx_2}{1-λ}\\ 3=\dfrac{y_1-λy_2}{1-λ} \end{array} \right. \)，
\(∵\overrightarrow{PD}=λ\overrightarrow{DQ}\)，

\(∴\left\{ \begin{array}{c} x_0=\dfrac{x_1+λx_2}{1+λ}\\ y_0=\dfrac{y_1+λy_2}{1+λ} \end{array} \right. \)，
(用到定比分点坐标公式：若点\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，\(\overrightarrow{AM} =λ\overrightarrow{MB}\)，则点\(M\)的坐标为\(\left(\dfrac{x_1+λx_2}{1+λ}，\dfrac{y_1+λy_2}{1+λ}\right)\))
\(∵P、Q\)在双曲线\(x^2-y^2=1\)上，
\(∴\left\{ \begin{array}{c} x_1^2-y_1^2=1\\ x_2^2-y_2^2=1 \end{array} \right. \)，
由\(①-λ^2②\)得\(x_1^2-λ^2 x_2^2-(y_1^2-λ^2 y_2^2 )=1-λ^2\)，
\(∴2x_0-3y_0=\dfrac{x_1-λx_2}{1-λ}\cdot \dfrac{x_1+λx_2}{1+λ}-\dfrac{y_1-λy_2}{1-λ}\cdot \dfrac{y_1+λy_2}{1+λ}=\dfrac{x_1^2-λ^2 x_2^2-(y_1^2-λ^2 y_2^2}{1-λ^2}=1\)，
\(∴\)点\(D\)总在定直线\(2x-3y-1=0\)上；
(解法过于巧妙，不如方法1来得自然)
 

方法3

从第2小问感觉到，该题应该存在一定的背景的，所以想找到其内在规律，避开大量的计算；
尝试用几何的方法处理，由\(\overrightarrow{AP}=λ\overrightarrow{AQ}\)，\(\overrightarrow{PD}=λ\overrightarrow{DQ}⟹λ=\dfrac{|AP|}{|AQ|}=\dfrac{|DP|}{|DQ|}\)，想到了相似三角形或四点共圆再用圆幂定理.

连接\(BP\)，过点\(Q\)作\(QE||BP\)交直线\(AB\)于\(E\)，交直线\(BD\)于点\(F\)，
设\(E(2，y_E)\)，\(P(x_1，y_1)\)，\(Q(x_2，y_2)\)，

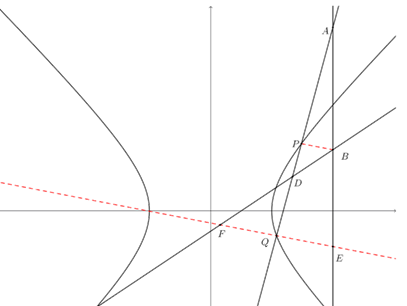
\(∵\overrightarrow{AP}=λ\overrightarrow{AQ}\)，\(\overrightarrow{PD}=λ\overrightarrow{DQ}\)，

\(∴λ=\dfrac{|AP|}{|AQ|}= \dfrac{|DP|}{|DQ|}\)，
\(∵QC||BP\)，

\(∴\dfrac{|AP|}{|AQ|}=\dfrac{|BP|}{|EQ|}\)，\(\dfrac{|DP|}{|DQ|}=\dfrac{|BP|}{|FQ|}\)，
(相似三角形中，\(A\)字型和\(8\)字型模型很常见，这也是作辅助线的思路来源)
\(∴\dfrac{|BP|}{|EQ|}=\dfrac{|BP|}{|FQ|}\)，\(∴|EQ|=|FQ|\)，即\(Q\)为\(EF\)中点，
\(∴F(2x_2-2，2y_2-y_E)\)，
\(∵\dfrac{|AP|}{|AQ|}=\dfrac{|AB|}{|AE|}=\dfrac{2}{3-y_E }\)，\(\dfrac{|AP|}{|AQ|}=\dfrac{x_1-2}{x_2-2}\)，

\(∴\dfrac{2}{3-y_E }=\dfrac{x_1-2}{x_2-2}⇒y_E=3-\dfrac{2(x_2-2)}{x_1-2 }\)，
\(∴k_{BF}=\dfrac{2y_2-y_E-1}{2x_2-4}=\dfrac{2y_2+\dfrac{2(x_2-2)}{x_1-2 }-4}{2x_2-4}=\dfrac{(x_1-2)(y_2-2)+x_2-2}{(x_1-2)(x_2-2)}\)，
(作出辅助线后，能猜测到动点\(D\)所在的定直线是过点\(B\)的，若\(k_{BF}\)是定值则证明成立)
设直线\(PQ\)方程为\(y=kx+m\)，其中\(m+2k=3\)，
(为了避免计算量过大，不要把直线设为\(y=k(x-2)+3\)再联立方程)
联立\(x^2-y^2=1\)，得\((k^2-1) x^2+2kmx+m^2+1=0\)，
则\(x_1+x_2=\dfrac{-2km}{k^2-1}\)，\(x_1 x_2=\dfrac{m^2+1}{k^2-1}\)，
\(∴k_{BF}=\dfrac{(x_1-2)(kx_2+m-2)+x_2-2}{(x_1-2)(x_2-2)}=\dfrac{kx_1 x_2+(m-2) x_1+(1-2k) x_2-2m+2}{x_1 x_2-2(x_1+x_2 )+4}\)\(=\dfrac{kx_1 x_2+(1-2k)(x_1+x_2 )-2m+2}{x_1 x_2-2(x_1+x_2 )+4}=\dfrac{k\cdot \dfrac{m^2+1}{k^2-1}+(1-2k)\cdot \dfrac{-2km}{k^2-1}-2m+2}{\dfrac{m^2+1}{k^2-1}-2\cdot \dfrac{-2km}{k^2-1}+4}\)

\(= \dfrac{k(m^2+1)-2km(1-2k)+(2-2m)(k^2-1)}{m^2+1+4km+4(k^2-1)}= \dfrac{(2m+2) k^2+(m-1)^2 k+2m-2}{4k^2+4km+m^2-3}\)

\(= \dfrac{(2m+2) k^2+(m-1)^2 k+2(m-3)+4}{(2k+m)^2-3}= \dfrac{[2k+(m-3)][(m+1)k+2]+4}{(2k+m)^2-3}\)

\(= \dfrac{0+4}{9-3}= \dfrac{2}{3}\)，
(计算量还是很大，还存在一定的运算技巧，不如方法1简洁，但它是第2小问通向简洁方法的路径)
\(∴\)直线\(BF\)的方程为\(y-1= \dfrac{2}{3}(x-2)\)，即\(2x-3y-1=0\)，
\(∴\)点\(D\)总在定直线\(2x-3y-1=0\)上；
 

第2小问

该问若直接切入求解(设\(BP\)方程—求点\(R\)坐标—求直线\(QR\)方程—确定定点)，计算量会很大；
所以思考是否存在简单些的方法，就考虑从几何的角度出发.
 

(在第1小问方法3的基础上解答)
设直线\(QR\)交直线\(BF\)于点\(G\)，交直线\(AB\)于点\(H\)，\(R(x_3，y_3)\)，\(G(x_4，y_4)\)，

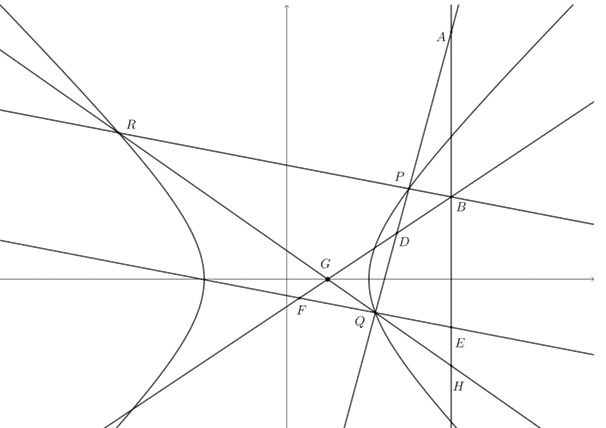
\(∵QE||BP\)，

\(∴\dfrac{|HQ|}{|HR|}=\dfrac{|EQ|}{|BR|}\)，\(\dfrac{|GQ|}{|GR|}=\dfrac{|FQ|}{|BR|}=\dfrac{|EQ|}{|BR|}\),

\(∴\dfrac{|HQ|}{|HR|}=\dfrac{|GQ|}{|GR|}\)，
(还是\(A\)字型和\(8\)字型)
\(∴\dfrac{|x_2-2|}{|x_3-2|}=\dfrac{|x_2-x_4|}{|x_3-x_4 |}\)，(注意加上绝对值)
\(∴|(x_2-2)(x_3-x_4 )|=|(x_3-2)(x_2-x_4 )|\)，
若\((x_2-2)(x_3-x_4 )=(x_3-2)(x_2-x_4 )\)，化简得\(x_4=2\)，显然不成立，
\(∴(x_2-2)(x_3-x_4 )=-(x_3-2)(x_2-x_4 )\)，
化简得\(2x_2 x_3-(x_4+2)(x_2+x_3 )+4x_4=0\)(※)，
设直线\(QR\)的方程为\(y=k_1 x+n\)，
联立\(x^2-y^2=1\),得\((k_1^2-1) x^2+2k_1 nx+n^2+1=0\)，
则\(x_2+x_3=\dfrac{-2k_1 n}{k_1^2-1}\)，\(x_2 x_3=\dfrac{n^2+1}{k_1^2-1}\)，
代入(※)得\(\dfrac{2n^2+2}{k_1^2-1}+\dfrac{2k_1 n}{k_1^2-1}(x_4+2)+4x_4=0\)，
由\(\left\{ \begin{array}{c} 2x-y-1=0\\ y=k_1 x+n \end{array} \right. \)，解得\(x=\dfrac{3n+1}{2-3k_1}\)，即\(x_4=\dfrac{3n+1}{2-3k_1}\)，
\(∴\dfrac{2n^2+2}{k_1^2-1}+\dfrac{2k_1 n}{k_1^2-1}\left(\dfrac{3n+1}{2-3k_1}+2\right)+4\cdot \dfrac{3n+1}{2-3k_1}=0\)，
\(⟹(2n^2+2)(2-3k_1 )+2k_1 n(3n-6k_1+5)+4(3n+1)(k_1^2-1) =0\)，
\(⟹4n^2+10k_1 n+4k_1^2-6k_1-12n=0\)，
\(⟹2n^2+5k_1 n+2k_1^2-3k_1-6n=0\)，
\(⟹(2n+k_1 )(n+2k_1 )-3(2n+k_1 )=0\)，
\(⟹(2n+k_1 )(n+2k_1-3)=0\)，
(运算过程中，因式分解是常用的技巧)
若\(n+2k_1-3=0\)时，则\(n=3-2k_1\)，
\(∴\)直线\(QR\)的方程为\(y=k_1 x+3-2k_1=k(x-2)+3\)，过点\(A(2，3)\)，故不成立；
\(∴2n+k_1=0⟹n=- \dfrac{1}{2} k_1\)，
\(∴\)直线\(QR\)的方程为\(y=k_1 x- \dfrac{1}{2} k_1=k_1 \left(x- \dfrac{1}{2}\right)\)，过定点\(\left(\dfrac{1}{2}，0\right)\).