三角函数中求参数ω的取值范围（保姆级教学）

根据某三角型函数\(f(x)=A\sin(ωx+φ)\)的单调性、对称性、最值等情况求参数\(ω\)的取值范围，对于高一刚学三角函数的学生来说难度较大；接下来我们展开保姆级的教学，在对比之下大家体会下：含参与不含参题目的方法或思路是差不多.
以下以\(f(x)=A\sin(ωx+φ)\)为例，\(f(x)=A\cos(ωx+φ)\)或\(f(x)=A\tan(ωx+φ)\)同理.
 
 

一 对称性问题

不含参三角函数

(多选题)以下哪个是函数\(f(x)=3\sin \left(2x+\dfrac{π}{4}\right)\)的对称轴 ( \(\qquad\) )
A．\(x=\dfrac{π}{8}\) \(\qquad \qquad\) B．\(x=\dfrac{π}{4}\) \(\qquad \qquad\) C．\(x=\dfrac{9π}{8}\) \(\qquad \qquad\) D．\(x=π\)
 

【解答】
方法1 复合函数转化法
令\(t=2x+\dfrac{π}{4}\)，(把\(2x+\dfrac{π}{4}\)看成整体)
选项\(A\)，判断题：\(x=\dfrac{π}{8}\)是函数\(f(x)=3\sin \left(2x+\dfrac{π}{4}\right)\)的对称轴 ( \(\qquad\) )
即相当于问“当\(x=\dfrac{π}{8}\)时，\(t=2x+\dfrac{π}{4}=\dfrac{π}{2}\)是否为\(y=\sin⁡x\)的对称轴”
(把函数\(y=A\sin(ωx+φ)\)的问题转化为\(y=\sin⁡x\)的问题)
显然\(x=\dfrac{π}{2}\)是\(y=\sin⁡x\)的对称轴，故\(A\)是对的；
当\(x=\dfrac{π}{4}\)时，\(t=2x+\dfrac{π}{4}=2×\dfrac{π}{4}+\dfrac{π}{4}=\dfrac{3π}{4}\)不是\(y=\sin⁡x\)的对称轴，故\(B\)是错的；
当\(x=\dfrac{9π}{8}\)时，\(t=2x+\dfrac{π}{4}=2×\dfrac{9π}{8}+\dfrac{π}{4}=\dfrac{5π}{2}\)是\(y=\sin⁡x\)的对称轴，故\(C\)是对的；
当\(x=π\)时，\(t=2x+\dfrac{π}{4}=2π+\dfrac{π}{4}=\dfrac{9π}{4}\)不是\(y=\sin⁡x\)的对称轴，故\(D\)是错的.
故选\(AC\).
 

方法2 求出函数所有对称轴
令\(2x+\dfrac{π}{4}=\dfrac{kπ}{2}+kπ\)(把\(2x+\dfrac{π}{4}\)看成整体，令其等于\(y=\sin⁡x\)的对称轴\(x=\dfrac{kπ}{2}+kπ\))
解得\(x=\dfrac{π}{8}+\dfrac{kπ}{2}\)，\(k\in Z\)，
选项\(A\)，判断题：\(x=\dfrac{π}{8}\)是函数\(f(x)=3\sin \left(2x+\dfrac{π}{4}\right)\)的对称轴 ( \(\qquad\) )
即相当于问“是否存在\(k_0\in Z\)，使得\(\dfrac{π}{8}=\dfrac{π}{8}+\dfrac{k_0π}{2}\)”，显然\(k_0=0\in Z\)，(\(k_0\)要是整数)
故\(A\)是对的；
选项\(B\)，判断题：\(x=\dfrac{π}{4}\)是函数\(f(x)=3\sin \left(2x+\dfrac{π}{4}\right)\)的对称轴 ( \(\qquad\) )
即相当于问“是否存在\(k_0\in Z\)，使得\(\dfrac{π}{4}=\dfrac{π}{8}+\dfrac{k_0π}{2}\)”，显然\(k_0=\dfrac{1}{4} \notin Z\)，故\(B\)是错的；
又\(k=2\)时，\(x=\dfrac{π}{8}+π=\dfrac{9π}{8}\)，故\(C\)是对的；
而\(\dfrac{π}{8}+\dfrac{kπ}{2}=π⟹k=\dfrac{7}{4} \notin Z\)，故\(D\)是错的；
故选\(AC\).
 

含参三角函数

已知函数\(f(x)=3\sin \left(ωx-\dfrac{π}{4}\right)(ω>0)\)的图象在\(\left[0，\dfrac{π}{2} \right]\)上恰有四个对称中心，则\(ω\)的取值范围为\(\underline{\quad \quad}\).
 

【解答】
方法1 复合函数转化法
令\(t=ωx-\dfrac{π}{4}\)，(把\(ωx-\dfrac{π}{4}\)看成整体)
\(∵0≤x≤\dfrac{π}{2}\)，则\(-\dfrac{π}{4}≤ωx-\dfrac{π}{4}≤\dfrac{πω}{2}-\dfrac{π}{4}⟹-\dfrac{π}{4}≤t≤\dfrac{πω}{2}-\dfrac{π}{4}\)，(求出整体\(t\)的范围)
因为函数\(y=f(x)\)在\(\left[0，\dfrac{π}{2} \right]\)上恰有四个对称中心，
所以函数\(y=\sin⁡x\)在\(\left[-\dfrac{π}{4}，\dfrac{πω}{2}-\dfrac{π}{4} \right]\)上恰有四个对称中心，
(把函数\(y=A\sin(ωx+φ)\)的问题转化为\(y=\sin⁡x\)的问题)

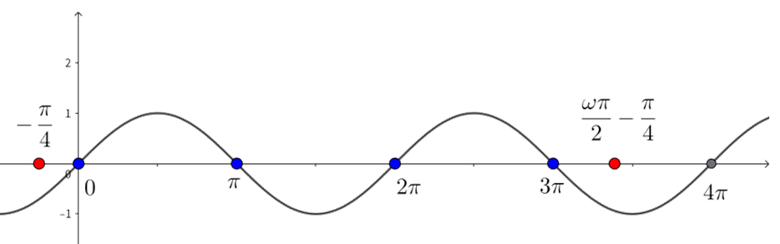
所以\(3π≤\dfrac{πω}{2}-\dfrac{π}{4}<4π\)，解得\(\dfrac{13}{2}≤ω<\dfrac{17}{2}\)，
即\(ω\)的取值范围为\(\left[\dfrac{13}{2}，\dfrac{17}{2}\right)\).
 

方法2 求出函数所有对称中心
令\(ωx-\dfrac{π}{4}=kπ\)，(把\(ωx-\dfrac{π}{4}\)看成整体，令其等于\(y=\sin⁡x\)的对称中心\((kπ，0)\)的横坐标)
解得\(x=\dfrac{π}{4ω}+\dfrac{kπ}{ω}\)，则\(y=f(x)\)的所有对称中心为\(\left(\dfrac{π}{4ω}+\dfrac{kπ}{ω}，0\right)\)；
\(y=f(x)\)的图象在\(\left[0，\dfrac{π}{2} \right]\)上恰有四个对称中心，
即在\(\left[0，\dfrac{π}{2} \right]\)上，恰存在连续四个\(k\in Z\)值使得\(\dfrac{π}{4ω}+\dfrac{kπ}{ω}\in \left[0，\dfrac{π}{2} \right]⟹\dfrac{1}{4ω}+\dfrac{k}{ω}\in \left[0，\dfrac{1}{2} \right]\)，
假设四个\(k\)中最小的为\(k_0\)，

则\(\left\{ \begin{array}{c} \dfrac{1}{4ω}+\dfrac{k_0-1}{ω}<0\\ \dfrac{1}{4ω}+\dfrac{k_0}{ω}>0\\ \dfrac{1}{4ω}+\dfrac{k_0+3}{ω}≤\dfrac{1}{2}\\ \dfrac{1}{4ω}+\dfrac{k_0+4}{ω}>\dfrac{1}{2} \end{array} \right. ⟹\left\{ \begin{array}{c} k_0<\dfrac{3}{4}\\ k_0>-\dfrac{1}{4}\\ ω≥2k_0+\dfrac{13}{2}\\ ω<2k_0+\dfrac{17}{2} \end{array} \right.\)，
(以\(ω\)为变量求解不等式)
解得\(\left\{ \begin{array}{c} -\dfrac{1}{4}<k_0<\dfrac{3}{4}\\ 2k_0+\dfrac{13}{2}≤ω<2k_0+\dfrac{17}{2} \end{array} \right. \),
(此处的难度较大，要注意利用好\(k_0\in Z\)和\(ω>0\)两个限制条件，把\(k_0\)的值求出)
而\(k_0\in Z\)，所以\(k_0=0\)，所以\(2k_0+\dfrac{13}{2}≤ω<2k_0+\dfrac{17}{2}⟹\dfrac{13}{2}≤ω<\dfrac{17}{2}\)；
即\(ω\)的取值范围为\(\left[\dfrac{13}{2}，\dfrac{17}{2}\right)\).

 

二 单调性问题

不含参三角函数

（多选题）以下哪个是函数\(f(x)=3\sin\left(2x+\dfrac{π}{4}\right)\)的增区间 ( \(\qquad\) )
A．\(\left(-\dfrac{11π}{8}，-\dfrac{7π}{8}\right)\) \(\qquad \qquad\) B．\(\left(-\dfrac{3π}{8}，\dfrac{π}{4}\right)\) \(\qquad \qquad\) C．\(\left(\dfrac{7π}{8}，\dfrac{9π}{8}\right)\) \(\qquad \qquad\) D．\(\left(\dfrac{11π}{8}，\dfrac{15π}{8}\right)\)
 

【解答】
方法1 复合函数转化法
令\(t=2x+\dfrac{π}{4}\)，(把\(2x+\dfrac{π}{4}\)看成整体)
选项\(A\)，判断题：\((-\dfrac{11π}{8}，-\dfrac{7π}{8})\)是函数\(f(x)=3\sin \left(2x+\dfrac{π}{4}\right)\)的增区间 ( \(\qquad\) )
即相当于问“当\(x\in \left(-\dfrac{11π}{8}，-\dfrac{7π}{8}\right)\)时，\(t=2x+\dfrac{π}{4}\in \left(-\dfrac{5π}{2}，-\dfrac{3π}{2}\right)\)是否为\(y=\sin⁡x\)的增区间”
(把函数\(y=A\sin(ωx+φ)\)的问题转化为\(y=\sin⁡x\)的问题)
显然为\(y=\sin⁡x\)在\(\left(-\dfrac{5π}{2}，-\dfrac{3π}{2}\right)\)上递增，故\(A\)是对的；
当\(x\in \left(-\dfrac{3π}{8}，\dfrac{π}{4}\right)\)时，\(t=2x+\dfrac{π}{4}\in \left(-\dfrac{π}{2}，\dfrac{3π}{4}\right)\)，\(y=\sin⁡x\)在\(\left(-\dfrac{π}{2}，\dfrac{3π}{4}\right)\)上不递增，故\(B\)是错的；
当\(x\in \left(\dfrac{7π}{8}，\dfrac{9π}{8}\right)\)时，\(t=2x+\dfrac{π}{4}\in \left(2π，\dfrac{5π}{2}\right)\)，\(y=\sin⁡x\)在\(\left(2π，\dfrac{5π}{2}\right)\)上递增，故\(C\)是对的；
当\(x\in \left(\dfrac{11π}{8}，\dfrac{15π}{8}\right)\)时，\(t=2x+\dfrac{π}{4}\in (3π，4π)\)，\(y=\sin⁡x\)在\((3π，4π)\)上不递增，故\(D\)是错的；
故选\(AC\).
 

方法2 求出函数所有增区间
令\(-\dfrac{π}{2}+2kπ≤2x+\dfrac{π}{4}≤\dfrac{π}{2}+2kπ\)，(把\(2x+\dfrac{π}{4}\)看成整体，把其代入\(y=\sin⁡x\)的增区间)
解得\(-\dfrac{3π}{8}+kπ≤x≤\dfrac{π}{8}+kπ\)，则\(y=f(x)\)的所有增区间\(\left(-\dfrac{3π}{8}+kπ，\dfrac{π}{8}+kπ\right)\)；
与判断函数对称轴的思路一样，
当\(k=-1\)时，增区间为\(\left(-\dfrac{11π}{8}，-\dfrac{7π}{8}\right)\)；当\(k=0\)时，增区间为\(\left(-\dfrac{3π}{8}，\dfrac{π}{8}\right)\)；
当\(k=1\)时，增区间为\(\left(\dfrac{5π}{8}，\dfrac{9π}{8}\right)\)；当\(k=2\)时，增区间为\(\left(\dfrac{13π}{8}，\dfrac{17π}{8}\right)\).
故选\(AC\).
 

含参三角函数

已知函数\(f(x)=3\sin \left(ωx+\dfrac{π}{4}\right)\)，其中\(ω>0\)．若\(f(x)\)在区间\(\left(\dfrac{π}{2}，\dfrac{3π}{4}\right)\)上单调递增，则\(ω\)的取值范围是\(\underline{\quad \quad}\).
 

【解答】
方法1 复合函数转化法
令\(t=ωx+\dfrac{π}{4}\)，(把\(ωx+\dfrac{π}{4}\)看成整体)
\(∵\dfrac{π}{2}<x<\dfrac{3π}{4}\)，

则\(\dfrac{π}{2}ω+\dfrac{π}{4}≤ωx+\dfrac{π}{4}≤\dfrac{3π}{4}ω+\dfrac{π}{4}⟹\dfrac{π}{2}ω+\dfrac{π}{4}≤t≤\dfrac{3π}{4}ω+\dfrac{π}{4}\)，(求出整体\(t\)的范围)
\(∵y=f(x)\)在区间\(\left(\dfrac{π}{2}，\dfrac{3π}{4}\right)\)上单调递增，
\(∴y=\sin⁡t\)在\(\left(\dfrac{π}{2}ω+\dfrac{π}{4}，\dfrac{3π}{4}ω+\dfrac{π}{4}\right)\)上单调递增，
(把函数\(y=A\sin(ωx+φ)\)的问题转化为\(y=\sin⁡x\)的问题)
则存在\(k_0\in Z\)，使得\(\left(\dfrac{π}{2}ω+\dfrac{π}{4}，\dfrac{3π}{4}ω+\dfrac{π}{4}\right)⊆ \left[-\dfrac{π}{2}+2k_0π，\dfrac{π}{2}+2k_0π \right]\)，
即\(\left\{ \begin{array}{c} \dfrac{π}{2}ω+\dfrac{π}{4}≥-\dfrac{π}{2}+2k_0π\\ \dfrac{3π}{4}ω+\dfrac{π}{4}≤\dfrac{π}{2}+2k_0π \end{array} \right. \)，解得\(-\dfrac{3}{2}+4k_0≤ω≤\dfrac{1}{3}+\dfrac{8}{3}k_0\)，
\(∴-\dfrac{3}{2}+4k_0≤\dfrac{1}{3}+\dfrac{8}{3}k_0\)，解得\(k_0<\dfrac{11}{8}\)，
\(∵ω>0\)，\(∴\dfrac{1}{3}+\dfrac{8}{3}k_0≥0\)，解得\(k_0≥-\dfrac{1}{8}\)，
\(∴-\dfrac{1}{8}≤k_0<\dfrac{11}{8}\)，
又因为\(k_0\in Z\)，所以\(k_0=0\)或\(1\)，
(此处的难度较大，要注意利用好\(k_0\in Z\)和\(ω>0\)两个限制条件，把\(k_0\)的值求出)
当\(k_0=0\)时，\(-\dfrac{3}{2}≤ω≤\dfrac{1}{3}\)，

又\(∵ω>0\)，则\(0<ω≤\dfrac{1}{3}\)，
当\(k_0=1\)时，\(\dfrac{5}{2}≤ω≤3\)，
\(∴ω\in \left(0，\dfrac{1}{3} \right]∪ \left[\dfrac{5}{2}，3 \right]\).
 

方法2 求出函数所有增区间
令\(-\dfrac{π}{2}+2kπ<ωx+\dfrac{π}{4}<\dfrac{π}{2}+2kπ\)，(把\(ωx+\dfrac{π}{4}\)看成整体，把代入\(y=\sin⁡x\)的增区间)
解得\(-\dfrac{3π}{4ω}+\dfrac{2kπ}{ω}<x<\dfrac{π}{4ω}+\dfrac{2kπ}{ω}\)，

则\(y=f(x)\)的所有增区间为\(\left(-\dfrac{3π}{4ω}+\dfrac{2kπ}{ω}，\dfrac{π}{4ω}+\dfrac{2kπ}{ω}\right)\)；
\(∵y=f(x)\)在区间\(\left(\dfrac{π}{2}，\dfrac{3π}{4}\right)\)上单调递增，
\(∴\)存在\(k_0\in Z\)，使得\(\left(\dfrac{π}{2}，\dfrac{3π}{4}\right)⊆ \left(-\dfrac{3π}{4ω}+\dfrac{2k_0π}{ω}，\dfrac{π}{4ω}+\dfrac{2k_0π}{ω}\right)\)，
即\(\left\{ \begin{array}{c} -\dfrac{3π}{4ω}+\dfrac{2k_0π}{ω}≤\dfrac{π}{2}\\ \dfrac{π}{4ω}+\dfrac{2k_0π}{ω}≥\dfrac{3π}{4} \end{array} \right. \)，解得\(-\dfrac{3}{2}+4k_0≤ω≤\dfrac{1}{3}+\dfrac{8}{3}k_0\)，
同方法1得\(ω\in\left(0，\dfrac{1}{3} \right]∪ \left[\dfrac{5}{2}，3 \right]\).
 

从以上两个例子，求解的方法主要有两个：复合函数法和求出函数的所以相应的性质，含参数的问题主要是利用好利用好\(k_0\in Z\)和\(ω>0\)两个限制条件，把\(k_0\)的值求出再求出参数\(ω\)的范围；对比而已，复合函数法更简单些.
那若以上的对称轴和单调性，换成最值或零点个数呢？思路是一样的，可以举一反三.我们接着看看综合问题.
 

三 综合问题

【例1】 已知函数\(f(x)=A\cos \left(ωx+\dfrac{π}{6}\right)(A>0，ω>0)\)，若\(f(x)\)在区间\(\left[0，2π \right]\)上有且仅有\(4\)个零点和\(1\)个最大值点，
则\(ω\)的取值范围是（ \(\qquad \qquad\) ）
A．\(\left[\dfrac{5}{3}，\dfrac{23}{12}\right)\) \(\qquad \qquad\) B．\(\left[\dfrac{11}{12}，\dfrac{23}{12}\right)\) \(\qquad \qquad\) C．\(\left[\dfrac{5}{3}，\dfrac{13}{6}\right)\) \(\qquad \qquad\) D．\(\left[\dfrac{23}{12}，\dfrac{13}{6}\right)\)
 

【解答】
由\(x\in \left[0，2π \right]\)，设\(t=ωx+\dfrac{π}{6}\in \left[\dfrac{π}{6}，2πω+\dfrac{π}{6} \right]\)；
\(f(x)\)在区间\(\left[0，2π \right]\)上有且仅有\(4\)个零点和\(1\)个最大值点，
即\(y=A\cos t\)在区间\(\left[\dfrac{π}{6}，2πω+\dfrac{π}{6} \right]\)上有且仅有\(4\)个零点和\(1\)个最大值点.
作出\(y=A\cos t\)的图象如图.

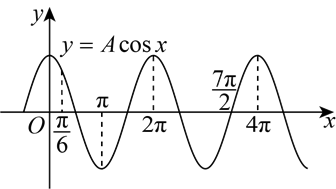
由\(f(x)\)在区间\(\left[0，2π \right]\)上有且仅有\(4\)个零点，得\(\dfrac{7π}{2}≤2πω+\dfrac{π}{6}<\dfrac{9π}{2}\)①；
又\(f(x)\)在区间\(\left[0，2π \right]\)上有且仅有\(1\)个最大值点，得\(2π≤2πω+\dfrac{π}{6}<4π\)②；
依题意需同时满足①②式，于是得\(\dfrac{7π}{2}≤2πω+\dfrac{π}{6}<4π\)，
即\(\dfrac{10π}{3}≤2πω<\dfrac{23π}{6}\)，解得\(\dfrac{5}{3}≤ω<\dfrac{23}{12}\)，
故\(ω\)的取值范围是\(\left[\dfrac{5}{3}，\dfrac{23}{12}\right)\).
故选：\(A\).
 

【例2】 已知函数\(f(x)=\sin \left(ωx+\dfrac{π}{3}\right)(ω>0)\)在\(\left(0，\dfrac{π}{3}\right)\)上存在零点，且在\(\left(\dfrac{2π}{3}，π\right)\)上单调递增，
则\(ω\)的取值范围为（ $\qquad \qquad $ ）
A．\((2，3]\) \(\qquad \qquad\) B．\(\left(2，\dfrac{13}{6} \right]\) \(\qquad \qquad\) C．\(\left[\dfrac{7}{4}，\dfrac{13}{6} \right]\) \(\qquad \qquad\) D．\(\left[\dfrac{7}{4}，3 \right]\)
 

【解答】 因为\(ω>0\)，当\(x\in \left(0，\dfrac{π}{3}\right)\)时\(ωx+\dfrac{π}{3}\in \left(\dfrac{π}{3}，\dfrac{π}{3}ω+\dfrac{π}{3}\right)\)，
由函数\(f(x)\)在\(\left(0，\dfrac{π}{3}\right)\)上存在零点，所以\(\dfrac{π}{3}ω+\dfrac{π}{3}>π\)，解得\(ω>2\)；
因为\(f(x)\)在\(\left(0，\dfrac{π}{3}\right)\)上单调递增，故\(\left\{ \begin{array}{c} \dfrac{2π}{3}ω+\dfrac{π}{3}≥-\dfrac{π}{2}+2kπ\\ πω+\dfrac{π}{3}≤\dfrac{π}{2}+2kπ) \end{array} \right. \)，\(k\in Z\)，
解得\(-\dfrac{5}{4}+3k≤ω≤\dfrac{1}{6}+2k\)，\(k\in Z\)；
显然\(-\dfrac{5}{4}+3k≤\dfrac{1}{6}+2k\)，所以\(k≤\dfrac{17}{12}\)；
当\(k≤0\)时，\(ω\)无解；当\(k=1\)时，可得\(2<ω≤\dfrac{13}{6}\)满足题意，
即\(ω\)的取值范围为\(\left(2，\dfrac{13}{6} \right]\).
故选：\(B\).
 

【例3】 将函数\(f(x)=\cos \left(x+\dfrac{2π}{3}\right)\)图象上所有点的横坐标变为原来的\(\dfrac{1}{ω}(ω>0)\)，纵坐标不变，所得图象在区间\(\left[0，\dfrac{2π}{3} \right]\)上恰有两个零点，且在\(\left[-\dfrac{π}{12}，\dfrac{π}{12} \right]\)上单调递减，则\(ω\)的取值范围为（ \(\qquad \qquad\) ）
A．\(\left[\dfrac{9}{4}，3 \right]\) \(\qquad \qquad\) B．\(\left[\dfrac{9}{4}，4\right)\) \(\qquad \qquad\) C．\(\left[\dfrac{11}{4}，4 \right]\) \(\qquad \qquad\) D．\(\left(\dfrac{11}{4}，6 \right]\)
 

【解答】 依题意可得\(y=\cos \left(ωx+\dfrac{2π}{3}\right)\)，
因为\(0≤x≤\dfrac{2π}{3}\)，所以\(\dfrac{2π}{3}≤ωx+\dfrac{2π}{3}≤\dfrac{2ω}{3}π+\dfrac{2π}{3}\)，
因为\(y=\cos \left(ωx+\dfrac{2π}{3}\right)\)在\(\left[0，\dfrac{2π}{3} \right]\)恰有\(2\)个零点，且\(\cos \left(\dfrac{π}{2}+k_1π\right)=0\)，\(k_1\in Z\)，
所以\(\dfrac{5π}{2}≤\dfrac{2ω}{3}π+\dfrac{2π}{3}<\dfrac{7π}{2}\)，解得\(\dfrac{11}{4}≤ω<\dfrac{17}{4}\)，
令\(2k_2π≤ωx+\dfrac{2π}{3}≤π+2k_2π\)，\(k_2\in Z\)，

得\(-\dfrac{2π}{3ω}+\dfrac{2k_2π}{ω}≤x≤\dfrac{π}{3ω}+\dfrac{2k_2π}{ω}\)，\(k_2\in Z\)，
令\(k_2=0\)，得\(y=\cos \left(ωx+\dfrac{2π}{3}\right)\)在\(\left[-\dfrac{2π}{3ω}，\dfrac{π}{3ω} \right]\)上单调递减，
所以\(\left[-\dfrac{π}{12}，\dfrac{π}{12} \right]⊆ \left[-\dfrac{2π}{3ω}，\dfrac{π}{3ω }\right]\)，
所以\(\left\{ \begin{array}{c} -\dfrac{2π}{3ω}≤-\dfrac{π}{12}\\ \dfrac{π}{3ω}≥\dfrac{π}{12} \end{array} \right. \)，又\(ω>0\)，解得\(0<ω≤4\)．
综上所述，\(\dfrac{11}{4}≤ω≤4\)，
故选：\(C\).