2022年深圳中学自招真题（答案版）

2022年深圳中学自招真题

全卷共15题，满分70分

   

1、(4分) 已知\(\dfrac{a}{b}=a+2\)，\(\dfrac{b}{a}=a-2\)，则\(\dfrac{b^2}{(a-2)^2 }=\)____．
【答案】 \(5\)
【解答】 将两式相乘得，\(a^2-4=1\)，即\(a^2=5\)；
又\(\dfrac{b}{a}=a-2⇒b=a(a-2)\)，所以\(\dfrac{b^2}{(a-2)^2 }=a^2=5\)．
【小结】 考核代数式变换；注意各式子的关系，比如和差积商是否为定值等；解方程组用到消元法.
 

2、(4分) 当\(x=14\)时，\(\sqrt{x-2+\sqrt{x-2+\sqrt{x-2+\sqrt{x+2}}}}=\)____．
【答案】 \(4\)
【解答】 \(\sqrt{x-2+\sqrt{x-2+\sqrt{x-2+\sqrt{x+2}}}}=\sqrt{14-2+\sqrt{14-2+\sqrt{14-2+\sqrt{14+2}}}}\)
\(=\sqrt{14-2+\sqrt{14-2+\sqrt{14+2}}} =\sqrt{14-2+\sqrt{14+2}} =\sqrt{14+2}=4\).
【小结】 考核代数式化简、二次根式.
 

3、(4分) 在\(△ABC\)中，\(∠A\)、\(∠B\)均为锐角，\(\sin⁡A= \dfrac{5}{13}\)，\(\tan⁡B=2\)，\(AB=29\)，则\(△ABC\)的面积\(S_{△ABC}=\)____．
【答案】 \(145\)
【解答】 设\(AB\)边上的高\(CD\)长为\(10x\)，则\(AD=24x\)，\(BD=5x\)，

故$AB=29x=29$，解得$x=1$， 故$S_{△ABC}= \dfrac{1}{2}×10×29=145$．

【小结】 考核三角函数；遇到三角函数，找直角三角形；设元求解.
 

4、(4分) 定义：（i）\(x⊗y=(x-1)⊗(y-1)+x+y\)；（ii）\(x⊗1=1\)．
则\((20⊗2)⊗2=\)____．
【答案】 \(26\)
【解答】 根据所给的两个递推关系式，有\(20⊗2=19⊗1+20+2=1+22=23\)，
进而，\(23⊗2=22⊗1+23+2=1+25+26\)．
【小结】 考核抽象概念，新定义问题.

 

5、(4分) 已知\(x、y\)为非零实数，且满足\(\left\{ \begin{array}{c} x=y+ \dfrac{1012}{x}\\ y=x+ \dfrac{1013}{y} \end{array} \right. \)，则\(|x-y|\)所有值之和为____．
【答案】 \(45\)
【解答】 将两式相加得，\(\dfrac{1012}{x}+ \dfrac{1013}{y}=0\)，
故设\(\dfrac{1012}{x}=- \dfrac{1013}{y}=k\)，则\(x= \dfrac{1012}{k}\)，\(y=- \dfrac{1013}{k}\)．
代回原方程组得\(\dfrac{1012}{k}=- \dfrac{1013}{k}+k\)，解得\(k^2=2025\)．
故\(|x-y|=| \dfrac{1012}{k}+ \dfrac{1013}{k}|= \dfrac{2025}{|k|}=45\)．
【小结】 考核方程；消元法、换元法.
 

6、(4分) 已知\(a^2+b^2+c^2=(a+b+c)^2\)，则\(\dfrac{b+c}{a}+ \dfrac{a+c}{b}+ \dfrac{a+b}{c}+100=\)____．
【答案】 \(97\)
【解答】 由\(a^2+b^2+c^2=(a+b+c)^2\)展开得，\(ab+bc+ca=0\)，
再除以\(abc\)得，\(\dfrac{1}{a}+ \dfrac{1}{b}+ \dfrac{1}{c}=0\)．
而\(\dfrac{b+c}{a}+ \dfrac{c+a}{b}+ \dfrac{a+b}{c}= \dfrac{a+b+c}{a}+ \dfrac{b+c+a}{b}+ \dfrac{a+b+c}{c}-3\)\(=(a+b+c)( \dfrac{1}{a}+ \dfrac{1}{b}+ \dfrac{1}{c})-3=-3\).
所以\(\dfrac{b+c}{a}+ \dfrac{a+c}{b}+ \dfrac{a+b}{c}+100=100-3=97\).
【小结】 考核代数式化简；三项平方公式\((a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)\).
 

7、(4分) 直线\(y= \dfrac{1}{17} x+a\)与\(x= \dfrac{1}{17} y+b\)交于\((42，43)\)，则\(a+b=\)____．
【答案】 \(80\)
【解答】 将两直线的方程式相加得，\(x+y= \dfrac{1}{17}(x+y)+(a+b)\)．
故\(a+b= \dfrac{16}{17}(x+y)= \dfrac{16}{17}(42+43)=80\).
【小结】 考核直线相交.
 

8、(4分) 如图，矩形\(ABCD\)中，\(AD=156\)，\(CD=65\)，\(BE\)平分\(∠ABC\)，则\(E\)到\(AC\)的距离为____．

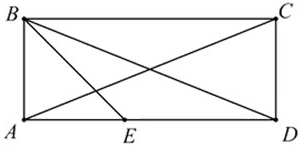
【答案】 \(25\)
【解答】 因为\(BE\)平分\(∠ABC\)，所以\(AE=AB=65\)，
过点\(E\)作\(EF⊥AC\)交\(AC\)于点\(F\)，
因为\(\sin⁡∠CAD= \dfrac{CD}{AC}= \dfrac{EF}{AE}\)，所以\(\dfrac{65}{\sqrt{65^2+156^2}}= \dfrac{EF}{65}\)，解得\(EF=25\).
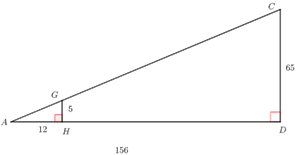
【小结】 考核几何综合，相似或三角函数；该题中貌似计算量很大，注意到\(65\)与\(156\)的最大公约数是\(13\)，其实\(AC\)很好求，把\(∆ACD\)缩小\(13\)倍，得到\(∆AGH\)，可得\(AG=13\)，则\(AC=13×13=169\).

 

9、(4分) 如图，在正方形\(ABCD\)中，\(PA=1\)，\(PB=2\)，\(PC=3\)，则\(∠APB\)的度数为____．

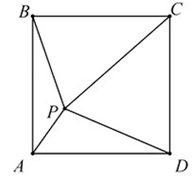
【答案】 \(135\)
【解答】 将\(△BAP\)绕\(B\)点逆时针旋转\(90^∘\)得\(△BCE\)，

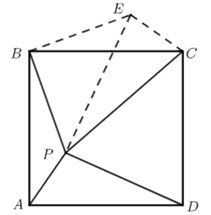
易知\(△BEP\)是等腰直角三角形，进而得\(EP=2\sqrt{2}\)，
再由\(EC=1\)及\(PC=3\)可知\(∠PEC=90^∘\)，
故\(∠APB=∠CEB=135^∘\)．
【小结】 考核平行四边形；手拉手模型的运用.
 

10、(4分) 若\(\dfrac{4}{15}< \dfrac{n}{6} <\dfrac{23}{7}\)，则所有满足条件的整数\(n\)的和为____．
【答案】 \(189\)
【解答】 若\(\dfrac{4}{15}< \dfrac{n}{6} <\dfrac{23}{7}\)，则\(\dfrac{24}{15}<n< \dfrac{138}{7}\)，

所以\(n\)的可能值为\(2，3，…，19\)，
所有满足条件的整数\(n\)的和为\(2+3+4+⋯+19= \dfrac{(2+19)×18}{2}=189\).
【小结】 考核不等式；等差数列\(\{a_n \}\)的前\(n\)项和\(S_n= \dfrac{(首项+末项)×项数}{2}\).
 

11、(6分) 若\(x-0.5\)不是整数，令\([x]\)最接近\(x\)的整数，如\([2.4]=2\)，\([2.6]=3\)，则
\([\sqrt{1×2}]+[\sqrt{2×3}]+[\sqrt{3×4}]+⋯+[\sqrt{22×23}]=\)____．
【答案】 \(253\)
【解答】 考虑通项式：\(\sqrt{n(n+1)}=\sqrt{\left(n+ \dfrac{1}{2}\right)^2- \dfrac{1}{4}} <n+ \dfrac{1}{2}\)，且\(\sqrt{n(n+1)}>n\)，
故有\([\sqrt{n(n+1)}]=n\)，
于是原式等于\(1+2+⋯…+22=253\)．
【小结】 考核新定义；这里用到了放缩技巧\(\sqrt{n(n+1)}=\sqrt{\left(n+ \dfrac{1}{2}\right)^2- \dfrac{1}{4}} <n+ \dfrac{1}{2}\).
 

12、(6分) 定义：\(f(x)=\dfrac{1}{\sqrt[3]{x^2+2x+1}+\sqrt[3]{x^2-1}+\sqrt[3]{x^2-2x+1}}\)，则\(f(1)+f(3)+⋯f(2k-1)+⋯+f(999)=\)____．
【答案】 \(5\)
【解答】 由立方差公式：\(a^3-b^3=(a-b)(a^2+ab+b^2 )\)，
设\(a=\sqrt[3]{x+1}\)，\(b=\sqrt[3]{x-1}\)，
则由\(f(x)= \dfrac{1}{a^2+ab+b^2} = \dfrac{a-b}{a^3-b^3} = \dfrac{\sqrt[3]{x+1}-\sqrt[3]{x-1}}{(x+1)-(x-1)} = \dfrac{1}{2}(\sqrt[3]{x+1}-\sqrt[3]{x-1})\)．
所求代数式等于\(\dfrac{1}{2}( \sqrt[3]{2}- \sqrt[3]{0}+ \sqrt[3]{4}- \sqrt[3]{2}+⋯ \sqrt[3]{1000}- \sqrt[3]{998})= \dfrac{1}{2}( \sqrt[3]{1000}- \sqrt[3]{0})=5\).
【小结】 考核根式化简；找到\(f(x)\)中的\(\sqrt[3]{x+1}\)，\(\sqrt[3]{x-1}\)，利用换元法，使得式子更简洁；用到了裂项求和法，常见的裂项公式\(\dfrac{1}{n(n+1)}= \dfrac{1}{n}- \dfrac{1}{n+1}\)，\(\dfrac{1}{n(n+k)} = \dfrac{1}{k}\left( \dfrac{1}{n}- \dfrac{1}{n+1}\right)\)，\(\dfrac{1}{\sqrt{n+1}+\sqrt{n}}=\sqrt{n+1}-\sqrt{n}\).
 

13、(6分) 设\(n\)为正整数，\(n^2+n+51\)是完全平方数，则所有\(n\)可能值之和等于____．
【答案】 \(55\)
【解答】 设\(k^2=n^2+n+51\)，\(k\)为整数，
为凑成\(n\)的完全平方数，\(4k^2=4n^2+4n+204=(2n+1)^2+203\)，
可运用平方差公式，得\((2k+2n+1)(2k-2n-1)=203×1=29×7\)，
于是得到两组方程组：\(\left\{ \begin{array}{c} 2k+2n+1=203\\ 2k-2n-1=1 \end{array} \right. \)或\(\left\{ \begin{array}{c} 2k+2n+1=29\\ 2k-2n-1=7 \end{array} \right.\)．
两方程相减，解得\(n=50\)或\(n=5\)．
【小结】 考核完全平方公式与平方差公式；设元法.

 

14、(6分) 已知\(x、y、z\)均为整数，\(x≤y≤z≤7\)，\(x+y+z=8\)，\(xy+yz+xz=-13\)，则\(|xyz|\)的值为____．
【答案】 \(140\)
【解答】 依题意可得\(8=x+y+z≤3z⇒z≥ \dfrac{8}{3}\)，又\(z≤7\)，
所以\(\dfrac{8}{3}≤z≤7\)，所以\(z\)的可能值为\(3，4，5，6，7\)，
当\(z=3\)时，\(x+y=5\)，\(xy=-28\)，
则\(x，y\)可以视为一元二次方程\(t^2-5t-28=0\)的两个实数根，
看方程是否存在两个整数根就行，若判别式不是完全平方数就可排除，提高解题速度，
该方程判别式\(∆=25+112=137\)，故排除；
当\(z=4\)时，\(x+y=4\)，\(xy=-29\)，排除；
当\(z=5\)时，\(x+y=3\)，\(xy=-28\)，排除；
当\(z=6\)时，\(x+y=2\)，\(xy=-25\)，排除；
当\(z=7\)时，\(x+y=1\)，\(xy=-20\)，
则\(x，y\)可以视为一元二次方程\(t^2-t-20=0\)的两个实数根，
方程解得\(t=5\)或\(-4\)，即\(x=-4\)，\(y=5\)，满足题意；
则\(|xyz|=|-4×5×7|=140\).
【小结】 考核代数；含\(3\)个未知数，只有\(2\)条方程，明确不能求出\(3\)个未知数；加上“\(x、y、z\)均为整数”，
可能想到用到穷举法，但范围有些广，先确定其中某个整数的取值范围，以简化列举.
 

15、(6分) 如图，在直角\(△ABC\)中，\(∠ACB=90^∘\)，\(AC=3\)，\(BC=4\).圆\(O_1\)与边\(AC\)和\(AB\)相切，
圆\(O_2\)与边\(BC\)和\(AB\)相切，圆\(O_1\)与圆\(O_2\)相外切，设圆心距\(O_1 O_2\)的最小值为\(m\)，则\(5m-m^2=\)____．

【答案】 \(15\)
【解答】 设圆\(O_1\)与圆\(O_2\)的半经为\(a\)和\(b\)，\(∠O_1 AB=α\)，\(∠O_2 BA=β\)，取\(AG=GO_1\)，\(BH=HO_2\)，作出下图，

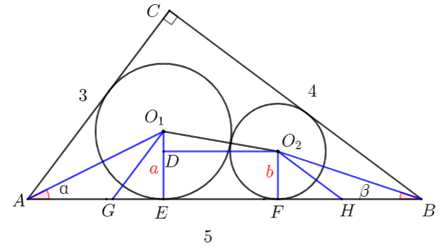
\(∵AG=GO_1\)，\(BH=HO_2\)，\(∴∠O_1 GE=2α\)，\(∠O_1 HF=2β\)，
易得\(ΔO_1 GE~ΔBAC\)，
\(∴O_1 G= \dfrac{5}{4} a\)，\(GE= \dfrac{3}{4} a\)，\(∴AE=AG+GE=O_1 G+GE=2a\)，
同理可得\(BF=3b\)，
(由高中的二倍角公式：\(\tan⁡2α= \dfrac{4}{3}⇒ \dfrac{2\tanα}{1-\tan^{2}α}= \dfrac{4}{3}⇒\tan⁡α= \dfrac{1}{2}\)，
\(\tan⁡2β= \dfrac{3}{4}⇒ \dfrac{2\tanβ}{1-\tan^{2⁡}β}= \dfrac{3}{4}⇒\tan⁡β= \dfrac{1}{3}\)，也可得\(AE=2a\)，\(BF=3b\))
又\(EF=O_2 D=\sqrt{O_1 O_2^2-O_1 D^2} =\sqrt{(a+b)^2-(a-b)^2 } =2\sqrt{ab}\)，
\(∴AB=AE+EF+BF=2a+3b+2\sqrt{ab}\)，
\(∴2a+3b+2\sqrt{ab}=5\)，
(现在问题变为已知\(2a+3b+2\sqrt{ab}=5\)，求\(a+b\)的最小值\(m\))
方法1
令所求的圆心距\(t=a+b\)，
则\(2t+b+2\sqrt{(t-b)b} =5\)，
所以\(2\sqrt{(t-b)b} =5-(2t+b)\)，
两边平方得，\(4tb-4b^2=4t2+b^2+25+4tb-20t-10b\)．
变形得\((2t-5)^2+5(b-1)^2=5\)．
当\((b-1)^2\)取最小值\(0\)，即\(b=1\)时，\(t\)可取到最小值\(m\)，
因此\(d\)的最小值\(m\)满足：\((2m-5)^2=5\)，
即\(4m^2-20m=-20⇒5m-m^2=5\)．
方法2
由\((\sqrt{xa} -\sqrt{yb} )^2≥0\)，得\(xa+yb≥2\sqrt{xyab}\)，
假设存在\(x>0\)，\(y>0\)使得\(2\sqrt{ab}≤xa+yb\)(当\(xa=yb\)时取到等号)，此时\(xy=1\)，
则\(2a+3b+2\sqrt{ab}=5⟺5≤2a+3b+xa+yb=(2+x)a+(3+y)b\)，
若\(2+x=3+y\)，则\(5≤(2+x)(a+b)⟺a+b≥ \dfrac{5}{2+x}\)，
由\(\left\{ \begin{array}{c} xy=1\\ 2+x=3+y \end{array} \right. \)，解得\(\left\{ \begin{array}{c} x= \dfrac{\sqrt{5} +1}{2} \\ y= \dfrac{\sqrt{5} -1}{2} \end{array} \right. \)，
所以\(a+b≥ \dfrac{5}{2+x} = \dfrac{5}{2+ \dfrac{\sqrt{5} +1}{2}} = \dfrac{5-\sqrt{5} }{2}\)，即\(m= \dfrac{5-\sqrt{5} }{2}\)，
所以\(5m-m^2=m(5-m)= \dfrac{5-\sqrt{5} }{2} ×\left(5- \dfrac{5-\sqrt{5} }{2} \right)= \dfrac{5-\sqrt{5} }{2} ×\dfrac{5+\sqrt{5} }{2} = \dfrac{20}{4} =5\)．
此时为了严谨，可检验下:不等式是否取到等号与这方法下\(a\)，\(b\)的值是否在题中存在(其实\(b\)最大能取到\(ΔABC\)
内切圆的半径\(\dfrac{3}{2}\))，最终也是当\(b=1\)，\(a= \dfrac{3-\sqrt{5}}{2}\)时取到最小值.
【小结】 考核综合分析；难度较大，要充分分析已知条件，尽量把问题进行等价转化.
方法2里有高中基本不等式的影子，若\(a>0\)，\(b>0\)，则\(a+b≥2\sqrt{ab}\).