圆的动点最值问题

专题：圆 $\qquad \qquad \qquad \qquad$ 题型：动点最值问题 $\qquad \qquad \qquad \qquad$ 难度系数：★★★

经典例题讲解尽量从学生的角度出发，重在引导思考与总结!

【题目】

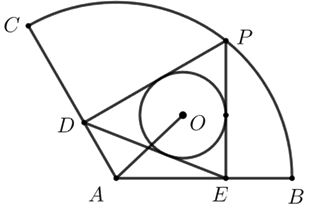
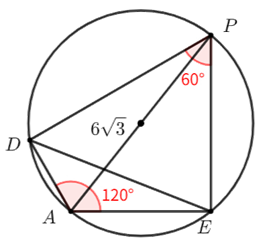
如图，扇形$ABC$中$∠BAC=120^\circ$，$AB=6\sqrt{3}$，点$P$是弧$BC$上一动点，过$P$作$PD⊥AC$，$PE⊥AB$，
连接$DE$，$O$是$∆PDE$的内心，则$AO$的最小值为$\underline{\quad \quad}$ .

【分析】

动点问题，首先了解运动状态，把动点$P$“动起来”，了解各量确定与否；
该题的图象具有较强对称性，故可猜测点$P$在弧$BC$中点时，$AO$取到最小值.

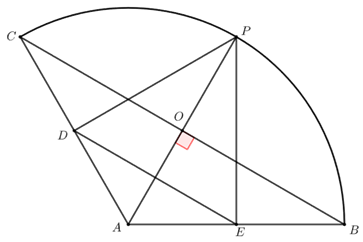
$AO_{min}=AB\times \sin⁡30^\circ=6\sqrt{3} ×\dfrac{1}{2}=3\sqrt{3}$.

1 分析已知条件
①$PD⊥AC$，$PE⊥AB$

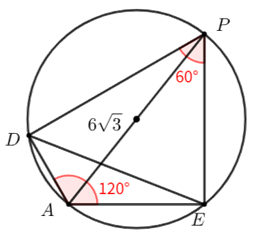
易得$P、D、A、E$四点共圆，从而得到半径为$\dfrac{AP}{2}=3\sqrt{3}$，$∠DPE=180^\circ-∠DAE=60^\circ$，
定圆中定圆周角所对的弦是确定的，即$DE$是定值；怎么求呢？
$DE=AP\cdot\sin⁡∠DPE=6\sqrt{3} ×\dfrac{\sqrt{3}}{2}=9$(此处用了高中正弦定理，可看后面的总结细讲).

②$O$是$∆PDE$的内心
遇到类似的已知条件，往往都会想到它的“定义与性质”；
由定义出发，可想到连接$OP$、$OE$(角平分线)或作$OG⊥DP$、$OH⊥PE$等；
由性质出发，会想到$\dfrac{1}{2} rC_{∆PDE}=S_{∆PDE}$(这在初中较为常见，后面的总结会给出证明)，
$∠DOE=180^\circ-\dfrac{180^\circ-∠DPE}{2}=90^\circ+\dfrac{∠DPE}{2}=120^\circ$等；
结合以上分析可继续思考，能否得到更多信息或思考角度.

2 分析求证
要求$AO$的最小值，
思考角度有① 点$A$是定点，确定动点$O$轨迹(初中轨迹一般是线段或圆)便可，这是常规思路；
② 利用$AO≥AP-OP=6\sqrt{3} -OP$，求$OP$的最大值，这想法符合一开始由图象对称性得到“点$P$在弧$BC$中点时，$AO$取到最小值”的猜测.

综上基本分析，会想到对$\dfrac{1}{2} rC_{∆DPE}=S_{∆DPE}$进一步思考，细看解答过程；
接着也作了各种尝试：
① 猜测动点$O$轨迹在线段$BC$上，依此为依据思考，只需证明$∠OBA=30^\circ$或者设线段$BC$与直线$OP$交于点$G$
再证明$GE$平分$∠DEP$，纯几何方法技巧性较强；
② 引入变量，表示点$O$的位置(比如内切圆半径，或图中某个角)，从而表示出$AO$再用代数方法求最小值或者确定点$O$轨迹是一种方法；
而建系法设点$P(m，n)$或$P(6\sqrt{3} \cos⁡⁡α，6\sqrt{3} \sin⁡α)$也可考虑，但计算量过大.

【解答】

方法一几何法

过点$O$作$OG⊥DP$，$OH⊥PE$，$OT⊥DE$，连接$OP$，

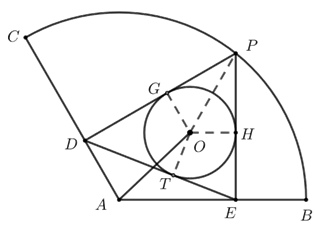
$∵PD⊥AC$，$PE⊥AB$，$∴P、D、A、E$四点共圆，

$∴∠DPE=180^\circ-∠BAC=60^\circ$，$DE=AP\cdot\sin⁡∠DPE=6\sqrt{3} ×\dfrac{\sqrt{3}}{2}=9$,
$∵O$是$∆PDE$的内心，设内切圆$O$的半径为$r$，
$∴∠OPH=\dfrac{1}{2}∠DPE=30^\circ⇒PH=\sqrt{3} r$，$OP=2r$，
$C_{∆PDE}=DP+DE+EP=(DG+DT)+(EH+ET)+(PG+PH)$
$=2DT+2ET+2PH=2DE+2\sqrt{3} r=2\sqrt{3} r+18$，
$\dfrac{1}{2} r C_{∆PDE}=S_{∆PDE}⇒\dfrac{1}{2} r(18+2\sqrt{3} r)=\dfrac{1}{2} DE\cdot h=\dfrac{9}{2} h$($h$为点$P$到$DE$的距离)，
而$h≤OP+OT=2r+r=3r$(当$A、O、P$三点共线时取到等号)，
$∴\dfrac{1}{2} r(18+2\sqrt{3} r)=\dfrac{9}{2} h≤\dfrac{27}{2} r$，
$∴r≤\dfrac{3\sqrt{3} }{2}$，
而$OA+OP≥AP$(当$A、O、P$三点共线时取到等号)，
即$OA+2r≥6\sqrt{3} ⇒OA≥6\sqrt{3} -2r≥6\sqrt{3} -2×\dfrac{3\sqrt{3} }{2}=3\sqrt{3}$.

方法二纯几何法求动点轨迹

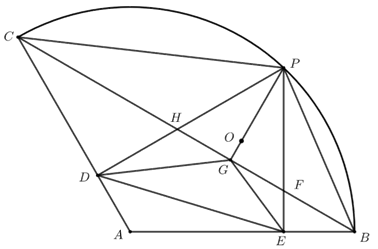
连接$BC$，设$OP$交$BC$于$G$，$PD$交$BC$于$H$，$PE$交$BC$于$F$，
(接着尝试证明$∠PEG=∠GED$从而得到$O$与$G$重合，即点$O$比在线段$BC$上)

$∵∠GPE=\dfrac{1}{2}∠DPE=30^\circ$，$∠ABC= \dfrac{180^\circ-∠BAC}{2}=30^\circ$，
$∴∠GPE=∠ABC$，
$∴G、E、B、P$四点共圆，易得$∆GFE \sim ∆PFB$，
$∴\dfrac{GE}{PB}=\dfrac{EF}{BF}=\sin30^\circ =\dfrac{1}{2}$，
同理$\dfrac{GD}{PC}=\dfrac{1}{2}$，
由方法1可得$DE=9$，在$∆ABC$中易得$BC=18$，$∴ \dfrac{DE}{BC}=\dfrac{1}{2}$，
$∴\dfrac{GE}{PB}=\dfrac{GD}{PC}= \dfrac{DE}{BC}$，$∴∆GDE \sim ∆PCB$，$∴∠GED=∠PBC$，
$∵G、E、B、P$四点共圆，$∴∠PEG=∠PBC$，
$∴∠PEG=∠GED$，即点$G$在$∠PED$的角平分线上，
又$∵$点$G$在$∠DPE$的角平分线上，
$∴$点$G$是$∆PDE$的内心，
又$∵O$是$∆PDE$的内心，
$∴$点$O$与点$G$重合，
$∴$点$O$比在直线$BC$上，(即点$O$的轨迹为线段$BC$上某一线段)
$∴AO$的最小值为点$A$到直线$BC$的距离$\dfrac{1}{2} AB=3\sqrt{3}$.
(严谨要检验下是否能够取到最小值的点$P$，其实就是当点$P$为弧$BC$中点的时候)

方法三建系法+求动点轨迹

预备知识：
① 斜率为$k$，且过点$(m，n)$的直线解析式为$y=k(x-m)+n$；
② 点$(x_0，y_0 )$到直线$Ax+By+C=0$的距离$d= \dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$.

以点$A$为原点，$AB$所在直线为$x$轴，如图建立直角坐标系，

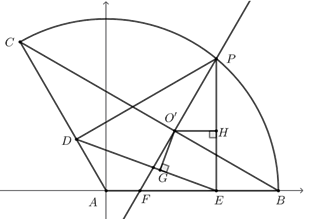
设点$P(m，n)$，直线$BC$与直线$OP$交于点$O'$，
由$AP=6\sqrt{3}$可得$m^2+n^2=108$，
同方法一可得$∠O' PE=30^\circ$，$∴∠PFE=60^\circ$，
$∴$直线$O' P$的解析式为$y=\sqrt{3} (x-m)+n$，
易得点$B(6\sqrt{3} ，0)$，$∠CBA=30^\circ$，
$∴$直线$BC$的解析式为$y=- \dfrac{\sqrt{3}}{3} x+6$，
由$\left\{ \begin{array}{c} y=\sqrt{3} (x-m)+n\\ y=- \dfrac{\sqrt{3}}{3} x+6 \end{array} \right. $，解得$\left\{ \begin{array}{c} x=\dfrac{\sqrt{3} }{4}(6+\sqrt{3} m-n)\\ y=6- \dfrac{1}{4} (6+\sqrt{3} m-n) \end{array} \right. $，
即点$O'$的坐标为$\left(\dfrac{\sqrt{3} }{4}(6+\sqrt{3} m-n)，6- \dfrac{1}{4} (6+\sqrt{3} m-n)\right)$，
$∵$直线$AC$的解析式为$y=-\sqrt{3} x$，直线$PD$的解析式为$y= \dfrac{\sqrt{3}}{3} (x-m)+n$，
由$\left\{ \begin{array}{c} y=-\sqrt{3} x\\ y= \dfrac{\sqrt{3}}{3} (x-m)+n) \end{array} \right. $，解得$\left\{ \begin{array}{c} x= \dfrac{m}{4}- \dfrac{\sqrt{3} n}{4} \\ y=- \dfrac{\sqrt{3} m}{4}+ \dfrac{3n}{4} \end{array} \right. $，
即点$D$的坐标为$\left(\dfrac{m}{4}-\dfrac{\sqrt{3}n}{4}，- \dfrac{\sqrt{3}m}{4}+ \dfrac{3n}{4}\right)$，
又$∵E(m，0)$，
$∴$直线$DE$的解析式为$y=\dfrac{m-\sqrt{3} n}{\sqrt{3} m+n} (x-m)⟹(\sqrt{3} m+n)y+(\sqrt{3} n-m)x+m(m-\sqrt{3} n)=0$，
$∴$点$O'(\dfrac{\sqrt{3} }{4}(6+\sqrt{3} m-n)，6- \dfrac{1}{4} (6+\sqrt{3} m-n))$到直线$DE$的距离为
$O'G= \dfrac{\left |(\sqrt{3} m+n)\left [6- \dfrac{1}{4} (6+\sqrt{3} m-n)\right]+(\sqrt{3} n-m)\cdot \dfrac{\sqrt{3} }{4}(6+\sqrt{3} m-n)+m(m-\sqrt{3} n)\right|}{\sqrt{(\sqrt{3} m+n)^2+(\sqrt{3} n-m)^2 }}$$=\dfrac{m+\sqrt{3} n-6\sqrt{3}}{4}$，
而点$O'$到直线$PE$的距离为$O' H=m-\dfrac{\sqrt{3} }{4}(6+\sqrt{3} m-n)=\dfrac{m+\sqrt{3} n-6\sqrt{3}}{4}$，
$∴O' G=O' H$，即点$O'$在$∠PED$的角平分线上，
而点$O'$也在$∠EPD$的角平分线上，
$∴$点$O'$是$∆PDE$的内心，即点$O$与点$O'$重合，即点$O$的轨迹为直线$BC$上某一线段，
$∴AO$的最小值为点$A$到直线$BC$的距离$\dfrac{1}{2} AB=3\sqrt{3}$.

【总结】

正弦定理：在$∆ABC$中，$\dfrac{a}{\sin⁡A} =\dfrac{b}{\sin⁡B} = \dfrac{c}{\sin⁡C}=2r$($r$为$∆ABC$外接圆的半径)

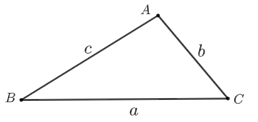
本题中求$DE$不要正弦定理，初中知识证明也可以，连接$OD$，延长$DO$交圆于点$G$，

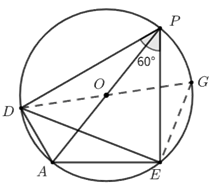
在$RT∆DGE$中，$DE=DG\cdot \sin⁡∠G=AP\cdot \sin⁡60^\circ=6\sqrt{3} ×\dfrac{\sqrt{3}}{2}=9$；
其实高中的正弦定理也可以采取近似方法证明.
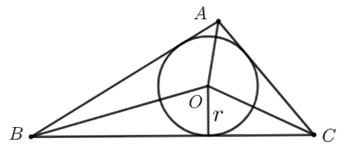
若点$O$是$∆ABC$内心，则$S_{∆ABC}=\dfrac{1}{2} rC_{∆ABC}$($r$为$∆ABC$内切圆的半径).
简证：如下图，$S_{∆ABC}=S_{∆AOB}+S_{∆BOC}+S_{∆AOC}=\dfrac{1}{2}\cdot r\cdot AB+\dfrac{1}{2}\cdot r\cdot BC+\dfrac{1}{2}\cdot r\cdot AC $$=\dfrac{1}{2}\cdot r(AB+BC+AC)=\dfrac{1}{2} rC_{∆ABC}$.

方法一中解答过程其实用到了两次不等式：$h≤OP+OT$和$OA+OP≥AP$，要注意严谨，它们取到等号的时候必须是同一情况下取到的.
其实动点$O$在直线$BC$上不受$∠BAC=120^\circ$，$AB=6\sqrt{3}$的影响.

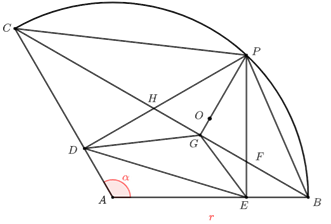
简证：如方法二，设$∠CAB=α$，$AB=r$，
$∵A，E，P，D$四点共圆，$∴DE=AP\cdot \sin⁡∠DPE=r\cdot \sin⁡(180^\circ-α)=r\cdot \sin⁡α$，
在$∆ABC$中，易得$BC=2AB\cdot \cos⁡⁡∠CBA=2AB\cdot \cos⁡⁡ \dfrac{180^\circ-α}{2} =2r\cdot \sin⁡ \dfrac{⁡⁡α}{2}$，
$∴ \dfrac{DE}{BC}=\dfrac{r\cdot \sin⁡α}{2r\cdot \sin⁡ \dfrac{⁡⁡α}{2}} =\cos \dfrac{⁡⁡α}{2}$，
$∵B，E，G，P$四点共圆，$∴∆GFE \sim ∆PFB$，

$∴\dfrac{GE}{PB}=\dfrac{EF}{BF}=\sin⁡\dfrac{180^\circ-α}{2} =\cos \dfrac{⁡⁡α}{2}$，
同理$\dfrac{DG}{PC}= \cos \dfrac{⁡⁡α}{2}$，
$∴ \dfrac{DE}{BC}=\dfrac{GE}{PB}= \dfrac{DG}{PC}$，$∴∆GDE \sim ∆PCB$，

$∴∠GED=∠PBC=∠GEP$，即点$G$在$∠PED$的角平分线上，
$∴$点$O$与点$G$重合，即点$O$比在直线$BC$上.

posted @ 2026-01-13 19:48 湛江贵哥讲数学阅读(1) 评论(0) 收藏举报

刷新页面返回顶部

湛江贵哥讲数学

自由教师一枚，乐于探讨数学、分享数学！ WX：mathszhg!

圆的动点最值问题

【题目】

【分析】