求三角函数参数ω的取值范围

专题：三角函数 \(\qquad \qquad \qquad \qquad\) 题型：求参数ω的取值范围 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★

【题目】

已知函数\(f(x)=\left|\cos \left(ω x+\dfrac{π}{3} \right)\right|(ω>0)\)在区间\(\left[-\dfrac{π}{3} ,\dfrac{5π}{6} \right]\)上单调递减，则\(ω\)的取值范围为\(\underline{\quad \quad}\).
 
 
 
 
 
 

【分析】

求解一题，要找到类似题型的“思考源泉”，

例：函数\(f(x)=\cos \left(2 x+\dfrac{π}{3} \right)\)的减区间为\(\underline{\quad \quad}\)

思路是：把\(2 x+\dfrac{π}{3}\)看成整体，把其代入\(y=\cos⁡x\)的单调减区间\((2kπ,π+2kπ)\)，

即\(2kπ<2x+\dfrac{π}{3} <π+2kπ (k\in Z)\)，求出\(x\)的范围便可；

有了这个基础，对于本题，先确定\(y＝|\cos x|\)的单调递减区间，再求出\(f(x)=\left|\cos \left(ω x+\dfrac{π}{3} \right)\right|\)的单调递减区间\((a，b)\)(含\(ω\)，\(k\))，
则\(\left[-\dfrac{π}{3} ，\dfrac{5π}{6} \right]⊆(a，b)\)，从而得到关于\(ω\)，\(k\)的不等式；

此时不等式含两个变量怎么办呢？看解题过程.
 

【解答】

由函数\(y=\cos⁡x\)的图象变换得到函数\(y＝|\cos x|\)图象

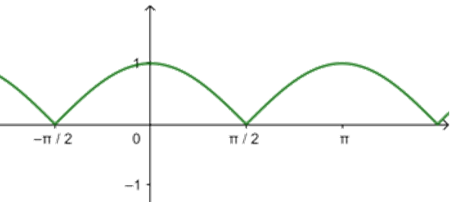
易得\(y＝|\ cos x|\)的单调递减区间为\(\left[kπ，kπ+\dfrac{π}{2} \right]\)，\(k\in Z\)，

由\(kπ≤ωx+\dfrac{π}{3} ≤kπ+\dfrac{π}{2}\)，\(k\in Z\)，得\(\dfrac{kπ-\dfrac{π}{3} }{ω} ≤x≤\dfrac{kπ+\dfrac{π }{6} }{ω}\)，

即函数的单调递减区间为\(\left[\dfrac{kπ-\dfrac{π}{3} }{ω} ，\dfrac{kπ+\dfrac{π }{6} }{ω} \right]\)，\(k\in Z\)，

\(∵f(x)\)在区间\(\left[-\dfrac{π}{3} ，\dfrac{5π}{6} \right]\)上单调递减，\(∴ \left[-\dfrac{π}{3} ，\dfrac{5π}{6} \right]⊆\left[\dfrac{kπ-\dfrac{π}{3} }{ω} ，\dfrac{kπ+\dfrac{π }{6} }{ω} \right]\)，

即\(\dfrac{kπ-\dfrac{π}{3} }{ω} ≤-\dfrac{π}{3}\)且\(\dfrac{kπ+\dfrac{π }{6} }{ω} ≥\dfrac{5π}{6}\)，解得\(\left\{ \begin{array}{c} ω≤\dfrac{6 }{5} k+\dfrac{1 }{5}\\ ω≤-3k+1 \end{array} \right. \)，\(k\in Z\)，

\(∵ω>0\)，

\(∴\dfrac{6 }{5} k+\dfrac{1 }{5} >0\)且\(-3k+1>0\)，解得\(- \dfrac{1}{6} <k< \dfrac{1}{3}\)，

又\(∵k\in Z\)，

\(∴k\)只能取\(0\)；

（不等式中含\(k\)、\(ω\)两个变量怎么办？但要注意\(k\in Z\)和\(ω>0\)确定\(k\)的值.）

当\(k=0\)时，\(\left\{ \begin{array}{c} ω≤\dfrac{1 }{5} \\ ω≤1 \end{array} \right. \)，即\(0<ω≤\dfrac{1 }{5}\)，

即\(ω\)的取值范围是\(\left(0，\dfrac{1 }{5} \right]\)．