函数与方程中的求参数或其范围 (21年湛江一中自主招生第24题)
专题:函数与方程 \(\qquad \qquad \qquad \qquad\) 题型:求参数或取值范围 \(\qquad \qquad \qquad \qquad\) 难度系数:★★★★
【题目】
(21年湛江一中自主招生) “凡此变数中函数彼变数者,则此为彼之函数”这是我们著名数学家李善兰给出的“(function)函数”翻译,一次函数、二次函数、反比例函数是初中阶段必须掌握的三大初等函数.
(1)已知实数\(m,n(m<n)\)在二次函数\(y=x^2+3x-4\)对称轴的同一侧,当\(m≤x≤n\)时,\(y\)的取值范围为\(\dfrac{12}{n}≤y≤\dfrac{12}{m}\),求出\(m\),\(n\)的值;
(2)已知直线\(y=2tx-2\)和抛物线\(y=(t^2-1)x^2-1\)在\(y\)轴左边相交于\(A\),\(B\)两点,点\(C\)是线段\(AB\)的中点,经过\(C\),\(D(-2,0)\)的直线交\(y\)轴于点\(H(0,h)\),求\(h\)的取值范围.
【分析】
第一问: \(y=x^2+3x-4\)的对称轴为\(x=-\dfrac{3}{2}\),依题意可知有两种情况:
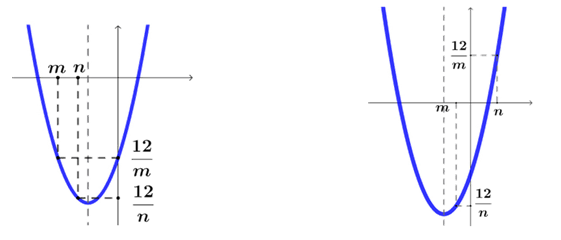
①当\(m<n<-\dfrac{3}{2}\)时,\(y\)随着\(x\)的增大而减小,有\(\left\{
\begin{array}{c}
m^2+3m-4=\dfrac{12}{m}\\
n^2+3n-4=\dfrac{12}{n}
\end{array}
\right.
\),要解这方程组,计算有些难度,思路:一是数形结合二是去分母因式分解,细看解答过程;
②当\(-\dfrac{3}{2}<m<n\)时,\(y\)随着\(x\)的增大而增大,有\(\left\{
\begin{array}{c}
n^2+3n-4=\dfrac{12}{m}\\
m^2+3m-4=\dfrac{12}{n}
\end{array}
\right.
\),要解这方程组,感觉比上一个更复杂了,自行多尝试下,有些技巧;
第二问:
(1)分析已知条件
① 一次函数与二次函数相交,
很容易想到联立方程\(\left\{
\begin{array}{c}
y=2tx-2\\
y=(t^2-1)x^2-1
\end{array}
\right.
\)得到\((t^2-1) x^2-2tx+1=0\),
②\(A\),\(B\)两点在\(y\)轴左侧
即\(x_A<0\),\(x_B<0\);
③ 点\(C\)是线段\(AB\)的中点
想到中点公式得到\(x_C=\dfrac{x_A+x_B}{2}\),
④ 经过\(C\),\(D(-2,0)\)的直线交\(y\)轴于点\(H(0,h)\)
想到求直线\(CD\)解析式(显然含\(t\)),则\(h\)可以用\(t\)表示;
(2)分析求证
求\(h\)的取值范围,由分析已知条件显然可知得到\(h\)用\(t\)表示的式子,利用函数思想求其范围便可.
此时思路很清晰了,设点\(A(x_1,y_1)\),\(B(x_2,y_2)\),由联立方程组可求出点\(C\)坐标,进而求出直线\(CD\)解析式,得到\(h\)可以用\(t\)表示,再求其范围.
但是其中具体求解也会多个角度和一些易错点.
【解答】
第一问:
函数\(y=x^2+3x-4\)的对称轴为\(x=-\dfrac{3}{2}\),分两种情况讨论:
① 当\(m<n<-\dfrac{3}{2}\)时,\(y\)随着\(x\)的增大而减小,有\(\left\{
\begin{array}{c}
m^2+3m-4=\dfrac{12}{m}\\
n^2+3n-4=\dfrac{12}{n}
\end{array}
\right.
\)(※),
则\(m\),\(n\)可看成方程\(x^2+3x-4=\dfrac{12}{x}⟹x^3+3x^2-4x-12=0\)的实数根,
方程变形得\(x^2 (x+3)-4(x+3)=0⟹(x+3)(x^2-4)=0\),
解得\(x=-3\),\(x=-2\),\(x=2\),
由于\(m<n<-\dfrac{3}{2}\),易得\(m=-3\),\(n=-2\);
求解方程组(※)使用了“分组分解的因式分解法”,有些技巧性;除此之外,还有其他角度:
(i) 从应试的角度,可尝试猜方程的解,一般从整数入手;如直接猜出\(-2\)和\(-3\)的值没证明,过程会被扣分,但若猜到\(x^3+3x^2-4x-12=0\)一个解为\(2\),进一步进行因式分解变形得\((x-2)(x^2+ax+6)=0\),先求出a再求出另外一个解\(-3\)和\(-2\);
(ii) 方程\(x^2+3x-4=\dfrac{12}{x}\)的实数根,可以理解为\(y=x^2+3x-4\)和\(y=\dfrac{12}{x}\)图象交点横坐标,但是我们也最多只能知道它是否有解,而不能求出具体的值;但这个角度也很重要,万一最后方程组是没实数根的呢!
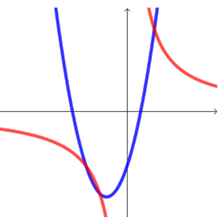
② 当\(-\dfrac{3}{2}<m<n\)时,\(y\)随着\(x\)的增大而增大,有\(\left\{
\begin{array}{c}
n^2+3n-4=\dfrac{12}{m} ①\\
m^2+3m-4=\dfrac{12}{n} ②
\end{array}
\right.
\)(※※),
由\(①×n-②×m\)得\(m^2 n-n^2 m+4m-4n=0⟹(m-n)(mn+4)=0\),
\(∵m≠n\),\(∴mn+4=0\),即\(m=- \dfrac{4}{n}\),
将\(m=- \dfrac{4}{n}\)代入方程②得,\(n^2+6n-4=0\),解得\(n=-3±\sqrt{13}\),
(求方程组(※※)也有多种尝试,比如①+②,①-②等试图消元,过程较为繁琐)
\(∵n>-\dfrac{3}{2}\),\(∴n=-3+\sqrt{13}\),
而\(m=- \dfrac{4}{n} =-3-\sqrt{13}<-\dfrac{3}{2}\),不满足\(m>-\dfrac{3}{2}\),
\(∴\)这种情况不存在满足题意的\(m\),\(n\),
综上可得\(m=-3\),\(n=-2\);
第二问:
依题意联立方程\(\left\{
\begin{array}{c}
y=2tx-2\\
y=(t^2-1)x^2-1
\end{array}
\right.
\)得到\((t^2-1) x^2-2tx+1=0\),
设点\(A(x_1,y_1)\),\(B(x_2,y_2)\),
则\(x_1+x_2=\dfrac{2t}{t^2-1}\),\(x_1 x_2=\dfrac{1}{t^2-1}\),\(y_1+y_2=2t(x_1+x_2 )-4=\dfrac{4t^2}{t^2-1}-4=\dfrac{4}{t^2-1}\),
(韦达定理)
\(∵\)点\(C\)是线段\(AB\)的中点,\(∴C(\dfrac{t}{t^2-1},\dfrac{2}{t^2-1})\),
(中点公式:点\(A(x_1,y_1)\),\(B(x_2,y_2)\)的中点\(C(\dfrac{x_1+x_2}{2} ,\dfrac{y_1+y_2}{2} )\))
设直线\(CD\)解析式为\(y=kx+b\),
代入\(C(\dfrac{t}{t^2-1},\dfrac{2}{t^2-1})\),\(D(-2,0)\)得\(\left\{
\begin{array}{c}
\dfrac{t}{t^2-1}\cdot k+b=\dfrac{2}{t^2-1}\\
-2k+b=0
\end{array}
\right.
\),解得\(\left\{
\begin{array}{c}
k=\dfrac{2}{2t^2+t-2}\\
b=\dfrac{4}{2t^2+t-2}
\end{array}
\right.
\),
\(∴h=\dfrac{4}{2t^2+t-2}\),
(接着求\(h\)的范围,用到函数思想,即求函数\(h(t)\)值域,要注意自变量\(t\)的范围即函数定义域)
\(∵A\),\(B\)两点在\(y\)轴左侧,\(∴x_1<0\),\(x_2<0\),
\(∴x_1+x_2<0\),\(x_1 x_2>0\),即\(\dfrac{2t}{t^2-1}<0\)且\(\dfrac{1}{t^2-1}>0\),解得\(t<-1\),
设\(T=2t^2+t-2\),其图象开口向上,对称轴为\(t=-\dfrac{1}{4}\)的抛物线,
当\(t<-1\)时,\(T\)随着\(t\)的增大而减小,
所以\(T>2\cdot (-1)^2-1-2=-1\),
\(∴\)当\(T>0\)时,\(h=\dfrac{4}{T} >0\);当\(-1<T<0\)时,\(h=\dfrac{4}{T} <-4\);
此处想到反比例函数\(h=\dfrac{4}{T} (T>-1)\),由图象较易想到要分类讨论,处处体现到函数思想
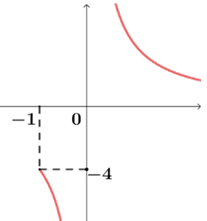
\(∴h\)的取值范围为\(h>0\)或\(h<-4\).
另一方法,得到方程\((t^2-1) x^2-2tx+1=0\)后,可用十字相乘法或求根公式求出实数根\(x_1=\dfrac{1}{t+1}\),\(x_2=\dfrac{1}{t-1}\);
要看得出方程实数根能求得出来,数感也要较强,含参方程的求解在高中也是基本功.
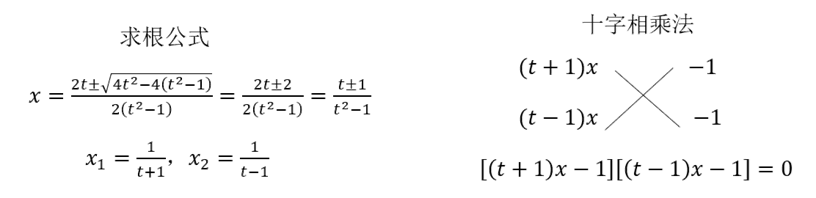


 浙公网安备 33010602011771号
浙公网安备 33010602011771号