二次函数角度问题（15年湛江一中自主招生第19题）

专题：二次函数 \(\qquad \qquad \qquad \qquad\) 题型：角度问题 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★
 

【题目】

(15年湛江一中自主招生第19题) 如图，在平面直角坐标系\(xOy\)中，顶点为\(M\)的抛物线是由抛物线\(y=x^2-3\)向右平移一个单位后得到的，它与\(y\)轴负半轴交于点\(A\)，点\(B\)在该抛物线上，且横坐标为\(3\)．
(1)求点\(M\)、\(A\)、\(B\)坐标；
(2)连接\(AB\)、\(AM\)、\(BM\)，求\(∠ABM\)的正切值；
(3)点\(P\)是顶点为\(M\)的抛物线上一点，且位于对称轴的右侧，设\(PO\)与\(x\)正半轴的夹角为\(α\)，当\(α=∠ABM\)时，求\(P\)点坐标．

 
 
 
 
 

【分析】

第一问： 由平移得到抛物线解析式\(y=(x-1)^2-3\)，点\(M\)、\(A\)、\(B\)坐标就不难求；
第二问： 由于点\(M\)、\(A\)、\(B\)是确定，则求\(∠ABM\)的正切值，完全由这三点确定，把图象简化为下图；

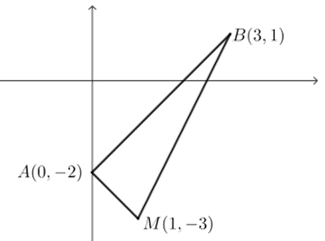
从已知条件出发，可尝试利用两点距离公式求出三条线段\(AB\)、\(AM\)、\(BM\)的长度，看看是否能确定它是个直角三角形；或观察三个点的坐标特点，会不会有一些特殊角度等；
从求证出发，要求\(∠ABM\)的正切值，第一个念头是找一直角三角形；
到了高中我们会学到解三角形(含正弦定理、余弦定理)，一旦一个三角形是确定的，它的边长或内角都可以求出来；但在初中往往都多观察图形的特殊性，比如它有木有一些特殊角度(\(30°\),\(45°\),\(60°\)等)或是否特殊三角形(直角三角形、等腰三角形等).

第三问： 第二问求出来，就意味着\(α\)的度数确定了，容易想到设元的方法求解；设点\(P(x,x^2-2x-2)\)，构建直角三角形，利用\(\tan⁡α=\tan⁡∠ABM\)求解；只是要注意点\(P\)可在\(x\)轴上方和下方.
 

【解答】

第一问： 抛物线\(y=x^2-3\)向右平移一个单位后得到的函数解析式为\(y=(x-1)^2-3\)，
顶点\(M(1,-3)\)，
令\(x=0\)，则\(y=(0-1)^2-3=-2\)，点\(A(0,-2)\)，
\(x=3\)时，\(y=(3-1)^2-3=4-3=1\)，点\(B(3,1)\)；
 

第二问： 方法1 过点\(B\)作\(BE⊥AO\)于\(E\)，过点\(M\)作\(MF⊥AO\)于\(M\)，

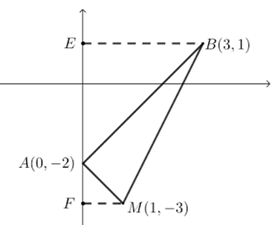
\(∵EB=EA=3\)，\(∴∠EAB=∠EBA=45°\)，
同理可求\(∠FAM=∠FMA=45°\)，
\(∴△ABE∽△AMF\)，\(∴\dfrac{AM}{AB}=\dfrac{AF}{AE}=\dfrac{1}{3}\)，
又\(∵∠BAM=180°-45°×2=90°\)，
\(∴\tan∠ABM=\dfrac{AM}{AB}=\dfrac{1}{3}\)；

方法2 由(1)得\(AB=3\sqrt2\)，\(AM=\sqrt2\)，\(BM=2\sqrt5\)，
\(∴BM^2=AB^2+AM^2=20\)，
\(∴∠BAM=180°-45°×2=90°\)，
\(∴\tan∠ABM=\dfrac{AM}{AB}=\dfrac{1}{3}\)；
 

第三问： 过点\(P\)作\(PH⊥x\)轴于\(H\)，

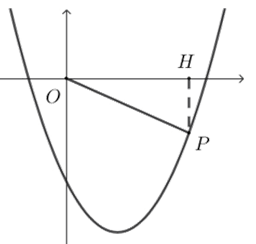
\(∵y=(x-1)^2-3=x^2-2x-2\)，

\(∴\)设点\(P(x,x^2-2x-2)\)，
① 点\(P\)在\(x\)轴的上方时，\(\dfrac{x^2-2x-2}{x}=\dfrac{1}{3}\)，整理得，\(3x^2-7x-6=0\)，
解得\(x_1=-\dfrac{2}{3}\)(舍去)，\(x_2=3\)，
\(∴\)点\(P\)的坐标为\((3,1)\)；
② 点\(P\)在\(x\)轴下方时，\(\dfrac{-(x^2-2x-2)}{x}=\dfrac{1}{3}\)，整理得，\(3x^2-5x-6=0\)，
解得\(x_1=\dfrac{5-\sqrt{97}}{6}\)(舍去)，\(x_2=\dfrac{5+\sqrt{97}}{6}\)，
\(x=\dfrac{5+\sqrt{97}}{6}\)时，\(x^2-2x-2=\dfrac{1}{3}(3x^2-5x-6)-\dfrac{1}{3}x=-\dfrac{1}{3}x=-\dfrac{1}{3}×\dfrac{5+\sqrt{97}}{6}=-\dfrac{5+\sqrt{97}}{18}\)，
\(∴\)点\(P\)的坐标为\((\dfrac{5+\sqrt{97}}{6}，-\dfrac{5+\sqrt{97}}{18})\)，
综上所述，点\(P\)的坐标为\((3,1)\)或\((\dfrac{5+\sqrt{97}}{6}，-\dfrac{5+\sqrt{97}}{18})\)．