动点问题中的定值与最值（2024年安徽省芜湖一中自主招生第17题）

专题：几何综合 \(\qquad \qquad \qquad \qquad\) 题型：动点问题中的定值与最值 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★★

 

【题目】

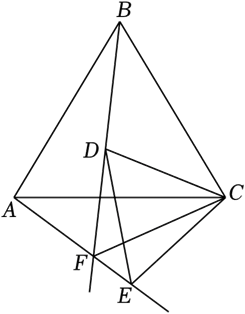
（2024年安徽省芜湖一中自主招生第17题） 如图，等边\(△ABC\)内有一动点\(D\)，\(△CDE\)是等边三角形(点\(B\)，\(E\)在直线\(AC\)两侧)，直线\(BD\)与直线\(AE\)交于点\(F\)．

(1)判断\(∠AFC\)的大小是否为定值？若是定值，求出其大小；若不是定值，请说明理由．

(2)若\(AB=5\)，\(CD=3\)，求线段\(AF\)长的最小值．

 
 
 
 
 

【分析】

第一问：

(1) 分析已知条件

可想到“手拉手”模型，得到\(△BCD≅△ACE\)，所以\(∠CAE=∠CBD\)，\(BD=AE\)，\(∠AEC=∠BDC\)，

而若注意到\( \begin{cases} ∠AEC=∠BDC \\ ∠BDC与∠CDF互补 \end{cases}\)\(⇒∠AEC\)与\(∠CDF\)互补，则\(D,C,E,F\)四点共圆，

所以\(∠CFE=∠CDE=60°\)，即\(∠AFC=120°\)；

这里就把问题解决了，若没想到四点共圆，在求证中也可以分析出来；
 

(2) 分析求证

① 判断\(∠AFC\)的大小是否为定值？大概率是定值，那是多少呢？

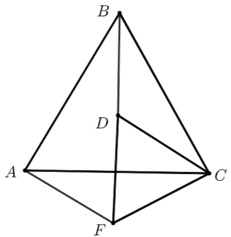
我们可取特殊情况考虑：当点\(D\)为\(△ABC\)的中心，易得题目图象变为下图，易得\(∠AFC=120°\)；

② 判断\(∠AFC\)的大小是否为定值？即判断\(∠CFE\)的大小是否为定值？

即\(∠CFE=60°\)，而\(∠CDE=60°\)，那只要证明\(D,C,E,F\)四点共圆便可；
 

第二问：

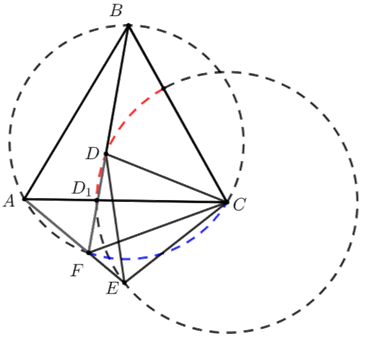
① 先了解题意，等边\(△ABC\)是确定的，由\(CD=3\)得动点\(D\)的轨迹是红色的弧线；

② 线段\(AF\)长的最小值：点\(A\)是定点，则最好确定点\(F\)的轨迹，

而\(D,C,E,F\)四点共圆，此时点\(F\)的轨迹为蓝色的弧线；

③ 不要想当然：当点\(D\)落在点\(D_1\)时线段\(AF\)长取到最小值；

④ 看到\(AB=5\)，\(CD=3\)，有勾股数\(3,4,5\)构造直角三角形的可能；

⑤ 应该把线段\(AF\)理解为\(△ABC\)外接圆的一条弦长，由同圆内弦所对的圆心角或圆周角越小它就越短，
即线段\(AF\)长取到最小时，\(∠ABF\)最小，即\(∠CBD=60°-∠ABF\)最大；

在\(△BCD\)中，\(BC=5\)，\(CD=3\)，要使得\(∠CBD\)最大，当然是当\(∠BDC=90°\)(即\(BD\)为圆\(C\)切线)时。

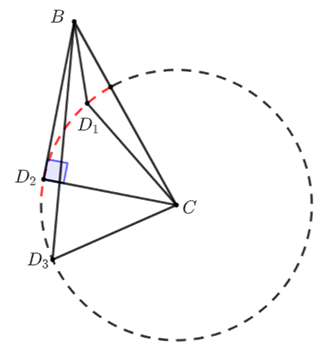
想到这里求线段\(AF\)长的最小值也很简单了；

当然要严谨的话，还要证明当\(∠BDC=90°\)(即\(BD\)为圆\(C\)切线)时，点\(D\)是在红色弧线上的。

(因为\(∠BD_1 C\)是锐角)

 

【解答】

第一问： \(∠AFC\)的大小是定值，大小为\(120°\)，理由如下：

\(∵△ABC\)和\(△CDE\)是等边三角形，

\(∴AC=BC\)，\(CE=CD\)，\(∠ACB=∠DCE=∠CDE=60°\)，

\(∴∠BCD=∠ACE\)，

\(∴△ACE≌△BCD(SAS)\)，

\(∴∠BDC=∠AEC\)，

\(∴C，D，F，E\)四点在同一圆上，

\(∴∠CFE=∠CDE=60°\)，

\(∴∠AFC=180°-∠CFE=120°\)；
 

第二问： 由(1)知\(∠AFC+∠ABC=120°+60°=180°\)，

\(∴A，F，C，B\)四点在同一圆上．

当\(∠CBF\)最大时，\(AF\)最小，当\(CD⊥BF\)时，\(∠CBF\)最大，

\(∵AB=5\)，\(CD=3\)，

\(∴BD=\sqrt{5^2-3^2}=4\)，

由(1)知\(△ACE≅△BCD\)，

\(∴AE=BD=4\)，\(∠AEC=∠BDC=90°\)，

\(∵CE=CD\)，\(CF=CF\)，

\(∴Rt△CEF≅Rt△CDF\)，

\(∴∠ECF=∠DCF=\dfrac{1}{2}∠DCE=30°\)，

\(∵\tan∠ECF=\tan30°=\dfrac{EF}{CE}=\dfrac{\sqrt3}{3}\)，

\(∴EF=\sqrt3\)，

\(∴AF=AE-EF=4-\sqrt3\)，

\(∴\)线段\(AF\)长的最小值为\(4-\sqrt3\)．