圆与相似的综合（2024年东莞市东华高级中学自主招生第23题）

专题：圆 \(\qquad \qquad \qquad \qquad\) 题型：相似+求比值 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★★

 

【题目】

（2024年东莞市东华高级中学自主招生第23题）

四边形\(ABCD\)内接于\(⊙O\)，\(AB=AD\)，对角线\(AC\)、\(BD\)相交于\(E\)点．

(1) 如图1，点\(F\)为\(AC\)上一点，\(∠BFC=2∠CFD=∠BAD\)．
  ① 求证：\(△ABF∽△DBC\)；   ② 求\(\dfrac{AF}{AC}\)的值．

(2) 如图2，求证：\(\dfrac{CD+BC}{BD}=\dfrac{AC}{AB}\)．

 
 
 
 
 
 

【分析】

1 第一问，先分析已知条件

①\(AB=AD\)：想到等腰三角形的性质，得\(∠ABD=∠ADB\)或三线合一(这需要作辅助线)；在圆上想到所对的圆周角或圆心角，\(∠ACD=∠ACB=∠ABD=∠ADB\)；

②\(∠BFC=2∠CFD=∠BAD\)：图中存在较多角度相等或倍数关系或线性关系，往往利用设元容易理清它们的关系；
设\(∠CFD=x°\)，则\(∠BFC=∠BAD=2x°\)，\(∠ACD=∠ACB=∠ABD=∠ADB=90°-x°\)，这样易得\(∠FDC=90°\)；
设元并在图中标注，最主要看理清各角关系，有助于寻找解题思路，滤清思路后在解题过程中不一定要设元；

如下图，

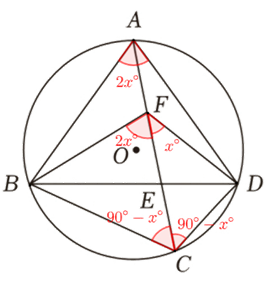
看到类似\(∠BFC=2∠CFD\)的倍角关系，也会想到把大角\(∠BFC\)平分或把小角\(∠CFD\)扩大两倍，再证明全等三角形或相似三角形之类思路。
 

接着分析求证

① 要证明\(△ABF∽△DBC\)：由于\(∠BAC=∠BDC\)，只需要证明\(∠BCD=∠AFB\)，这个由上图容易证明：\(∠BCD=∠BCA+∠ACD=180°-2x°=∠AFB\)；

② 求\(\dfrac{AF}{AC}\)的值：想到利用第一问，\(△ABF∽△DBC⟹\left\{ \begin{array}{c} ∠ABF=∠BCD⟹∠ABD=∠BFC\\ \dfrac{AF}{CD}=\dfrac{AB}{BD}=\dfrac{BF}{BC} \end{array} \right.\)，

接下来需要技巧与对图象的观察能力，具体看解析求解；

 

2 第二问，较为明显的思路有：

① 题目是一脉相承的，第一问中的结论应该有用，知道\(\dfrac{AF}{AC}\)的值，那就知道\(\dfrac{AF}{FC}\)的值；

由\(△ABF∽△DBC\)，得到一些比值，要直接向要证明的\(\dfrac{CD+BC}{BD}=\dfrac{AC}{AB}\)靠拢有些难度，具体看解析；

② 从要求证的\(\dfrac{CD+BC}{BD}=\dfrac{AC}{AB}\)入手，出现线段相加\(CD+BC\)，比较容易想到延长\(DC\)到\(G\)，使得\(CG=BC\)，
则只需要证明\(\dfrac{DG}{BD}=\dfrac{AC}{AB}\)，进而只要证明\(∆BDG∽∆BAC\)；

由于易得\(∠BAC=∠BDC\)，故只需要证明\(∠G=∠ACB\)，这个易证.

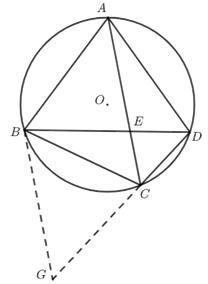
这么证明出来了，那第一问结论没用上，应该不是出题者思路，方法有两种，具体看解析.
 

【解答】

第一问 ① 证明：\(∵ABCD\)是圆内接四边形，\(∴∠BCD=180°-∠BAD\)，

\(∵∠BFA\)与\(∠BFC\)是邻补角，\(∴∠BFA=180°-∠BFC\)，

又\(∵∠BAD=∠BFC\)，\(∴∠BCD=∠BFA\)， (这些角的关系得益于分析1中的设元)

又\(∵∠BAC=∠BDC\)，

\(∴△ABF∽△DBC\)；

②解：方法1 作\(∠BFC\)的角平分线交\(BC\)于点\(G\)，则\(∠CFG=\dfrac{1}{2}∠BFC=∠CFD\)，

(遇到倍角关系，可或把大角分成小角或把小角扩大成大角，再证明全等或相似三角形)

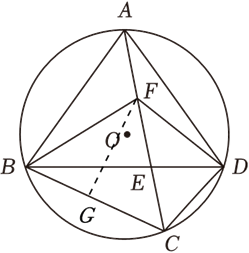
\(∵AB=AD\)，\(∴∠ACB=∠ACD\)，
\(∵CF=CF\)，\(∴△FCG≌△FCD(ASA)\)，
\(∴CG=CD\)，
\(∵∠CBD=∠ABF\)，\(∴∠ABD=∠FBC=∠ACD=∠ACB\)，
\(∴FB=FC\)，
\(∴FG\)垂直平分\(BC\)，\(∴BC=2CG=2BG=2CD\)，
\(∵△ABF∽△DBC\)，\(∴\dfrac{BF}{AF}=\dfrac{BC}{CD}=2\)，
\(∴BF=2AF=CF\)，
\(∴AC=AF+CF=3AF\)，
\(∴\dfrac{AF}{AC}=\dfrac{1}{3}\)．
 

方法2 过点\(A\)作\(AH⊥BD\)，交\(BD\)于\(H\)，

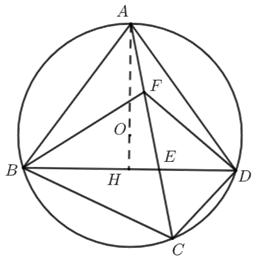
\(∵AB=AD\)，\(∴BD=2DH\)，\(∠HAD=\dfrac{1}{2}∠BAD=∠CFD\)，
(等腰三角形性质的运用)

设\(∠CFD=x°\)，则\(∠BFC=∠BAD=2x°\)，
又\(∵AB=AD\)，\(∴∠ACD=∠ACB=∠ABD=∠ADB=90°-x°\)，
\(∴∠FDC=180°-∠CFD-∠FCD=180°-x°-(90°-x°)=90°\)；
\(∴∠FDC=∠AHD\)，
\(∵△AHD∽△FDC\)，\(∴\dfrac{CF}{CD}=\dfrac{AD}{DH}=\dfrac{AD}{\dfrac{1}{2}DB}=\dfrac{2AB}{DB}\)，
由①\(△ABF∽△DBC\)，\(∴\dfrac{AF}{CD}=\dfrac{AB}{DB}\)，
\(∴\dfrac{CF}{CD}=\dfrac{2AF}{CD}\)，\(∴CF=2AF\)，
\(∴\dfrac{AF}{AC}=\dfrac{1}{3}\)．

 
第二问 证明：

方法1 延长\(DC\)到\(G\)，使得\(CG=BC\)，

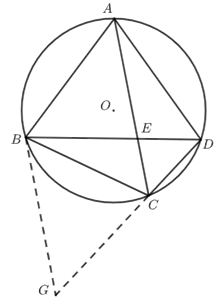
\(∴∠G=\dfrac{180°-∠BCG}{2}\)，

\(∵∠ACD=∠ACB\)，\(∴∠ACB=\dfrac{180°-∠BCG}{2} =∠G\)，

又\(∵∠BAC=∠BDC\)，\(∴∆BAC∽∆BDC\)，

\(∴\dfrac{DG}{BD}=\dfrac{AC}{AB}\)，即\(\dfrac{CD+BC}{BD}=\dfrac{AC}{AB}\)．
 

方法2 在\(AC\)上截取点\(F\)，使\(∠ABF=∠CBD\)，连接\(BF\)，

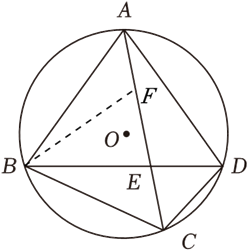
由(1)①知\(△ABF∽△DBC\)，\(∴\dfrac{AB}{BD}=\dfrac{AF}{CD}\)，

\(∴AF\times BD=AB\times CD\)... ...①

由(1)②知\(∠ABD=∠FBC=∠ACD=∠ACB=∠ADB\)，

\(∴△FBC∽△ABD\)，

\(∴\dfrac{AD}{CF}=\dfrac{BD}{BC}\)，

\(∴BD\times CF=AD\times BC\)... ...②

①+②得，\(AF\times BD+BD\times CF=AB\times CD+AD\times BC\)，

\(∵AB=AD\)，

\(∴BD\times(AF+CF)=AB\times(CD+BC)\)，

即\(BD\times AC=AB\times(CD+BC)\)，

\(∴\dfrac{CD+BC}{BD}=\dfrac{AC}{AB}\)．