抛物线+圆的存在性问题（25年广州越秀区执信中学自主招生第19题）

专题：二次函数+圆 \(\qquad \qquad \qquad \qquad\) 题型：存在性问题 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★★
 

【题目】

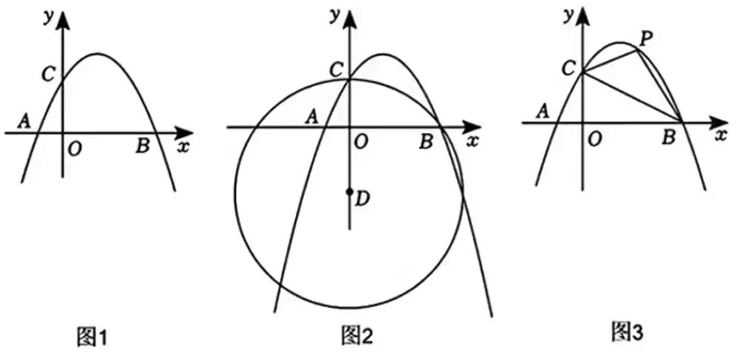
(25年广州越秀区执信中学自主招生第19题) 如图1，抛物线\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+c\)与\(x\)轴交于\(A\)，\(B\)两点，与\(y\)轴交于点\(C\)，且点\(A\)坐标为\((-1,0)\).
(1) 求抛物线解析式；
(2) 如图2，\(y\)轴上存在一点\(D\)，使\(⊙D\)经过\(B\)，\(C\)两点，求点\(D\)的坐标；
(3) 如图3，连接\(BC\)，点\(P\)(不与\(A\)，\(B\)，\(C\)三点重合)为抛物线上一动点，连接\(BP\)，在点\(P\)运动过程中，是否能够使得\(∠PBC=45°\)？若存在，求出此时点\(P\)的坐标，若不存在，请说明理由.

 
 
 
 
 

【分析】

第一问：把点\(A\)坐标为\((-1，0)\)代入抛物线\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+c\)中，则\(c=2\)，即可得抛物线的解析式；
第二问：由于\(⊙D\)经过\(B\)，\(C\)两点，则\(DB=DC\)，设\(D(0，y)\)，根据两点间距离公式列方程即可求解；
第三问：第三问比较有意思，有如下几点分析：
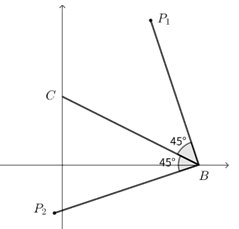
① 该问题，由于点\(B\)，\(C\)是固定的，则可理解为\(PB\)从\(BC\)开始顺时针或逆时针绕着点\(B\)旋转\(45°\)，若直线\(BP\)与抛物线有交点，即点\(P\)存在；

② 由①的分析，要求点\(P\)的坐标，容易想到思路：求出直线\(BP\)的方程，再与抛物线联立方程求解便可；
要求直线\(BP\)方程，而已知点\(B(4，0)\)，那只需要再求出\(k_{BP}\)或点\(P\)坐标(或直线上一点)；

那具体怎么求呢？在初中多数都是从几何的角度入手，多观察图形；
③ 看到\(∠PBC=45°\)，容易想到构造等腰直角三角形，以求点\(P_1\)为例，
(i)可过点\(C\)作\(CE⊥BC\)，有等腰直角三角形\(CEB\)(图1)，

方法1 待定系数法
由图1，设点\(E(m，n)\)，由\(CE=EB=\dfrac{BC}{\sqrt{2}} =\sqrt{10}\)求出点\(E\)坐标，再由\(B(4，0)\)，得到直线\(EB\)方程；

方法2 四点共圆
由图2，\(C\)，\(O\)，\(B\)，\(E\)四点共圆，且圆心为\(BC\)的中点\(H(2，1)\)，半径为\(\dfrac{1}{2} BC=\sqrt{5}\)，
则\(∠COB=∠PBC=45°\)，则\(∠EOB=45°\)，
设点\(E(m，m)\)，由\(EH=\sqrt{5}\)求出点\(E\)坐标，从而得到直线\(EB\)方程；
也可以用相似的方法.

(ii)可过点\(P\)作\(PE⊥BC\)，有等腰直角三角形\(P_1 EB\)(图1)，

 

方法1 三垂直模型
如图2，易得\(∆P_1 EF≅∆EGB\)，则\(P_1 F=EG\)，\(EF=BG\)，
由直线\(BC\)方程：\(y=-\dfrac{1}{2} x+2\)，设点\(E(t，-\dfrac{1}{2} t+2)\)，
则可求出点\(P_1\)坐标\((\dfrac{1}{2} t+2，6-\dfrac{3}{2} t)\)，代入抛物线，求点\(P_1\)坐标；
 

方法2 相似法
如图3，过点\(P_1\)作\(P_1 G⊥OB\)，易得\(∆P_1 EF~∆FGB\)，设\(FG=x\)，\(EF=y\)，
则\(BG=2x\)，\(BF=\sqrt{5} x\)，\(EP_1=2y\)，
因为\(EP_1=EB\)，所以\(2y=y+\sqrt{5} x⟹y=\sqrt{5} x\)，
则\(P_1 F=\sqrt{5} y=5x=5FG\)，所以\(P_1 G=6FG\)，
设点\(P_1 (t，-\dfrac{1}{2} t^2+\dfrac{3}{2} t+2)\)，
则\(-\dfrac{1}{2} t^2+\dfrac{3}{2} t+2=6(-\dfrac{1}{2} t+2)\)，求出t的值求出点\(P_1\)坐标.
判定点\(P_1\)是否存在或求出坐标后，求点\(P_2\)可用类似的方法求解，但多注意图形，有更简便的方法：
因为\(∠P_2 BC=45°\)，所以\(∠P_1 BP_2=90°\)，所以\(k_{EB}k_{P_2 B}=-1\)，
前面求出了\(k_{EB}\)，则\(k_{P_2 B}\)便可确定，得到直线\(P_2 B\)方程.
 

【解答】

第一问： 把点\(A\)坐标为\((-1，0)\)代入抛物线\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+c\)中，则\(-\dfrac{1}{2} -\dfrac{3}{2} +c=0\)，得\(c=2\)，
故抛物线的解析式为：\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2\)．
 

第二问： \(∵⊙D\)经过\(B\)，\(C\)两点，则\(DB=DC\)，

设\(D(0，y)\)，则\(BD^2=(0-y)^2+42=16+y^2\)，\(CD^2=(2-y)^2\)，
\(∴16+y^2=(2-y)^2\)，解得：\(y=-3\)，
故点\(D\)坐标为\((0，-3)\)．
 

第三问：
方法1 待定系数法
证明：在点\(P\)运动过程中，存在能够使得\(∠PBC=45°\)的点\(P\)，理由如下：

① 设当\(P_1\)点在\(x\)轴上方抛物线上时，设\(∠P_1 BC=45°\)，
令\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2=0\)，解得\(x_1=-1\)，\(x_2=4\)，
故点\(B(4，0)\)，
又\(C(0，2)\)，\(∴BC=2\sqrt{5}\)，
过点\(C\)作\(CE⊥BC\)，得到等腰直角三角形\(ECB\)，

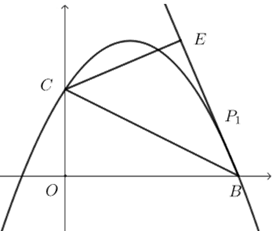
\(∴CE=EB=\dfrac{BC}{\sqrt{2}} =\sqrt{10}\)，
设点\(E(m，n)\)，\(m>0\)，\(n>0\)，
则\(\left\{ \begin{array}{c} (m-4)^2+n^2=10\\ m^2+(n-2)^2=10 \end{array} \right.\)，解得\(\left\{ \begin{array}{c} m=3\\ n=3 \end{array} \right.\)或\(\left\{ \begin{array}{c} m=1\\ n=-1 \end{array} \right.\)(舍去)，(※)
\(∴\)点\(E(3，3)\)，
设直线\(EB\)的方程为\(y=kx+b\)，则\(\left\{ \begin{array}{c} 3k+b=3\\ 4k+b=0 \end{array} \right.\)，解得\(\left\{ \begin{array}{c} k=-3\\ b=12 \end{array} \right.\)，
即直线\(EB\)的方程为\(y=-3x+12\)，
由\(\left\{ \begin{array}{c} y=-3x+12\\ y=-\dfrac{1}{2} x2+\dfrac{3}{2} x+2 \end{array} \right.\)得到\(x^2-9x+20=0\)，解得\(x=4\)或\(x=5\)，
此时点\(P_1 (4，0)\)或\((5，-3)\)，均不符合题意，即点\(P_1\)不存在；
② 设当\(P_2\)点在\(x\)轴下方抛物线上时，设\(∠P_2 BC=45^\circ\)，则\(∠P_2 BP_1=90^\circ\)，
所以\(k_{P_1 B}k_{P_2 B}=-1\)，而由①可得\(k_{P_1 B}=-3\)，则\(k_{P_2 B}=\dfrac{1}{3}\)，

(若不用\(k_{P_1 B}k_{P_2 B}=-1\)，也由方程(※)易得\(P_2 B\)上有个点\((1，-1)\)，可求出直线\(P_2 B\)方程)

所以直线\(P_2 B\)的方程为\(y= \dfrac{1}{3} x-\dfrac{4}{3}\)，
由\(\left\{ \begin{array}{c} y= \dfrac{1}{3} x-\dfrac{4}{3} \\ y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2 \end{array} \right.\)，解得：\(\left\{ \begin{array}{c} x=-\dfrac{5}{3}\\ y=-\dfrac{17}{9} \end{array} \right.\)，
即点\(P\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．
综上所述，点\(P\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．
 

方法2 四点共圆
证明：在点\(P\)运动过程中，存在能够使得\(∠PBC=45^\circ\)的点\(P\)，理由如下：

① 设当\(P_1\)点在\(x\)轴上方抛物线上时，设\(∠P_1 BC=45^\circ\)，
令\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2=0\)，解得\(x_1=-1\)，\(x_2=4\)，
故点\(B(4，0)\)，
又\(C(0，2)\)，\(∴BC=2\sqrt{5}\)，
过点\(C\)作\(CE⊥BC\)，得到等腰直角三角形\(ECB\)，连接\(OE\)，

又\(∵∠O=90^\circ\)，\(∴C\)，\(O\)，\(B\)，\(E\)四点共圆，
\(∴\)点\(E\)在以\(BC\)中点\(H(2，1)\)为圆心，半径为\(\dfrac{1}{2} BC=\sqrt{5}\)的圆上，
\(∴∠COE=∠P_1 BC=45^\circ\)，\(∴∠BOE=45^\circ\)，
可设点\(E(t，t)\)，
又\(EH=\sqrt{5}\)，\(∴(t-2)^2+(t-1)^2=5\)，解得\(t=3\)或\(t=0\)(舍去)；
\(∴\)点\(E(3，3)\)，
后面方法同方法1.
 

方法3 三垂直模型
证明：在点\(P\)运动过程中，存在能够使得\(∠PBC=45^\circ\)的点\(P\)，理由如下：

① 设当\(P_1\)点在\(x\)轴上方抛物线上时，设\(∠P_1 BC=45^\circ\)，
过点\(P_1\)作\(P_1 E⊥BC\)，过点\(E\)作\(EG⊥OB\)交\(x\)轴于\(G\)，过点\(P_1\)作\(P_1 F⊥EG\)交\(EG\)于\(F\)，

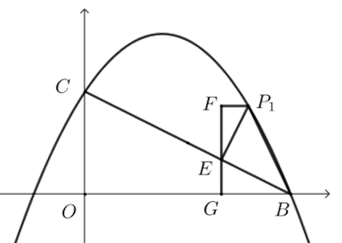
\(∵P_1 E⊥BC\)，\(EG⊥OB\)，\(∴∠P_1 EF=∠EBG\)，
又\(∵P_1 E=EB\)，\(∠EGB=∠F\)，\(∴∆P_1 EF≅∆EBG\)，
令\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2=0\)，解得\(x_1=-1\)，\(x_2=4\)，
故点\(B(4，0)\)，
设\(l_{BC}:y=kx+b\)，代入\(B(4，0)\)，\(C(0，2)\)，
可得\(\left\{ \begin{array}{c} b=2\\ 4k+b=0 \end{array} \right.\)，解得\(\left\{ \begin{array}{c} k=-\dfrac{1}{2}\\ b=2 \end{array} \right.\)，
故\(l_{BC}:y=-\dfrac{1}{2} x+2\)，
设\(E(t，-\dfrac{1}{2} t+2)\)，
\(∵∆P_1 EF≅∆EBG\)，
\(∴P_1 F=EG=-\dfrac{1}{2} t+2\)，\(EF=BG=4-t\)，
\(∴\)点\(P\)坐标为\((\dfrac{1}{2} t+2，6-\dfrac{3}{2} t)\)，
把点\(P(\dfrac{1}{2} t+2，6-\dfrac{3}{2} t)\)代入抛物线\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2\)中，
发现点\(P\)不在抛物线\(y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2\)图象上，
故点\(P\)不存在；
②设当\(P_2\)点在\(x\)轴下方抛物线上时，设\(∠P_2 BC=45^\circ\)，
过点\(C\)作\(CE⊥P_2 B\)，得到等腰直角三角形\(ECB\)，过点\(E\)作\(EF⊥OC\)，过点\(B\)作\(BG⊥EF\)于\(G\)，

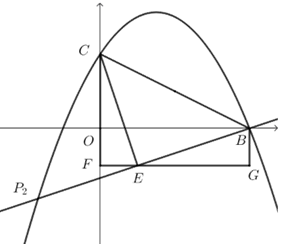
\(∵CE=BE\)，易证\(△CEF≌△EBG\)，
\(∴EF=BG\)，\(CF=EG\)，
设\(EF=BG=a\)，\(CF=EG=b\)，
则\(\left\{ \begin{array}{c} a+b=4\\ b-a=2) \end{array} \right.\)，解得：\(\left\{ \begin{array}{c} a=1\\ b=3 \end{array} \right.\)，\(∴\)点\(E\)坐标为\((1，-1)\)，
又\(B(4，0)\)，\(∴\)直线\(P_2 B\)的方程：\(y= \dfrac{1}{3} x-\dfrac{4}{3}\)，
联立\(\left\{ \begin{array}{c} y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2\\ y= \dfrac{1}{3} x-\dfrac{4}{3} \end{array} \right.\)，解得：\(\left\{ \begin{array}{c} x=-\dfrac{5}{3} \\ y=-\dfrac{17}{9} \end{array} \right.\)，即点\(P_2\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．
综上所述，点\(P\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．
(其实先求出点\(P_2\)再判断点\(P_1\)会更简洁些，因为求点\(P_2\)时，得到直线\(P_2 B\)的方程：\(y= \dfrac{1}{3} x-\dfrac{4}{3}\) ，那得到直线\(P_1 B\)的方程也会很容易)

 

方法4 相似法
证明：在点\(P\)运动过程中，存在能够使得\(∠PBC=45^\circ\)的点\(P\)，理由如下：

① 设当\(P_1\)点在\(x\)轴上方抛物线上时，设\(∠P_1 BC=45^\circ\)，
过点\(P_1\)作\(P_1 E⊥BC\)，过点\(P_1\)作\(P_1 G⊥OB\)交\(x\)轴于\(G\)，交\(BC\)于\(F\)，

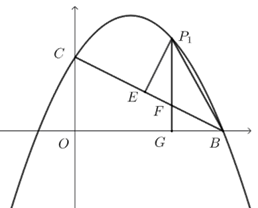
\(∵∠O=∠BGF=90^\circ\)，\(∴\tan ⁡∠GBG=\dfrac{GF}{BG}=\dfrac{OC}{OB}=\dfrac{1}{2}\)，
\(∵∠P_1 EF=∠BGF=90^\circ\)，\(∠P_1 FE=∠BFG\)，\(∴∆P_1 EF~∆FGB\)，
\(∴\dfrac{EF}{P_1 E}=\dfrac{GF}{BG}=\dfrac{1}{2}\)，
设\(FG=x\)，\(EF=y\)，则\(BG=2x\)，\(BF=\sqrt{5} x\)，\(EP_1=2y\)，
\(∵EP_1=EB\)，\(∴2y=y+\sqrt{5} x⟹y=\sqrt{5} x\)，
则\(P_1 F=\sqrt{5} y=5x=5FG\)，所以\(P_1 G=6FG\)，
设点\(P_1 (t，-\dfrac{1}{2} t^2+\dfrac{3}{2} t+2)\)，则\(-\dfrac{1}{2} t^2+\dfrac{3}{2} t+2=6(-\dfrac{1}{2} t+2)\)，解得\(t=4\)或\(t=5\)，
\(∴\)点\(P(4，0)\)或\((5，-3)\)，都不符合题意；
② 设当\(P_2\)点在\(x\)轴下方抛物线上时，设\(∠P_2 BC=45^\circ\)，
过点\(C\)作\(CG⊥BP_2\)，连接\(CG\)交\(OB\)于\(E\)，过点\(G\)作\(GF⊥OB\)交\(x\)轴于\(F\)，

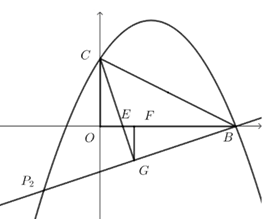
设\(OE=a\)，则\(CE=\sqrt{a^2+4}\)，\(EB=4-a\)，
\(∵∠O=∠BGC=90^\circ\)，\(∠CEO=∠BEG\)，\(∴∆P_1 EF~∆FGB\)，
\(∴\dfrac{OC}{BG}=\dfrac{OE}{EG}=\dfrac{CE}{EB}\)，
\(∴\dfrac{2}{BG}=\dfrac{a}{EG}=\dfrac{\sqrt{a^2+4}}{4-a}\)，
\(∴BG=\dfrac{2(4-a)}{\sqrt{a^2+4}}\)，\(EG=\dfrac{a(4-a)}{\sqrt{a^2+4}}\)，
又\(∵CG=BG\)，
\(∴\sqrt{a^2+4}+\dfrac{a(4-a)}{\sqrt{a^2+4}} =\dfrac{2(4-a)}{\sqrt{a^2+4}}\)，解得\(a=\dfrac{2}{3}\)，
\(∴OE=\dfrac{2}{3}\)，\(CE=\sqrt{a^2+4}=\dfrac{2\sqrt{10}}{3}\)，\(EG=\dfrac{a(4-a)}{\sqrt{a^2+4}}=\dfrac{\sqrt{10}}{3}\)，
易得\(∆COE~∆EFG\)，且相似比为\(\dfrac{CE}{EG}=2\)，
\(∴EF=\dfrac{1}{3}\)，\(GF=1\)，∴点\(G(1，-1)\)，
又\(B(4，0)\)，可得直线\(GB\)的方程：\(y= \dfrac{1}{3} x-\dfrac{4}{3}\)，
联立\(\left\{ \begin{array}{c} y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2\\ y= \dfrac{1}{3} x-\dfrac{4}{3} \end{array} \right.\)，解得：\(\left\{ \begin{array}{c} x=-\dfrac{5}{3} \\ y=-\dfrac{17}{9} \end{array} \right.\)，即点\(P_2\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．
综上所述，点\(P\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．

 

方法5 高中方法
预备知识
1 直线的倾斜角与斜率
当直线\(l\)与\(x\)轴相交时，取\(x\)轴作为基准，\(x\)轴正向与直线\(l\)向上方向之间所成的角\(α\)叫做直线\(l\)的倾斜角.

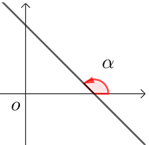
直线的斜率就是直线倾斜角的正切值，记作\(k=\tan α(α≠ 90^∘)\).
2 正切函数的两角和差公式：\(\tan ⁡(α±β)=\dfrac{\tan ⁡α±\tan ⁡β}{1∓\tan ⁡α\tan ⁡β}\)；
3 \(\tan ⁡(180^\circ-α)=-\tan ⁡α\).
证明： 在点\(P\)运动过程中，存在能够使得\(∠PBC=45^\circ\)的点\(P\)，理由如下：

① 设当\(P_1\)点在\(x\)轴上方抛物线上时，设\(∠P_1 BC=45^\circ\)，\(∠OBC=α\)，

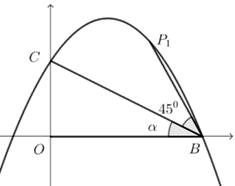
则\(\tan ⁡α=\dfrac{ OC}{OB}=\dfrac{1}{2}\)，
\(∴\tan ⁡∠P_1 BO=\tan ⁡(α+45^\circ)=\dfrac{\tan ⁡α+\tan ⁡45^\circ}{1-\tan ⁡α\tan ⁡45^\circ} =1-\dfrac{\dfrac{1}{2} +1}{1-\dfrac{1}{2}}=3\)，
\(∴k_{P_1 B}=\tan ⁡(180^\circ-∠P_1 BO)=-\tan ⁡∠P_1 BO=-3\)，
又\(B(4，0)\)，\(∴\)直线\(EB\)的方程为\(y=-3x+12\)，
由\(\left\{ \begin{array}{c} y=-3x+12\\ y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2 \end{array} \right.\)得到\(x^2-9x+20=0\)，
解得\(x=4\)或\(x=5\)，不符合题意，即点\(P\)不存在；
② 设当\(P_2\)点在\(x\)轴下方抛物线上时，设\(∠P_2 BC=45^\circ\)，\(∠OBC=α\)，

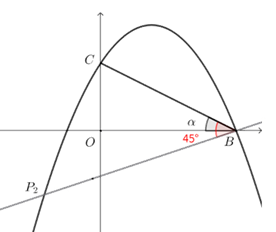
则\(\tan ⁡α=\dfrac{ OC}{OB}=\dfrac{1}{2}\)，
\(∴\tan ⁡∠P_2 BO=\tan ⁡(45^\circ-α)=\dfrac{\tan ⁡45^\circ-\tan ⁡α}{1+\tan ⁡45^\circ\tan ⁡α} =\dfrac{1-\dfrac{1}{2}}{1+\dfrac{1}{2}}=-\dfrac{1}{3}\)，
\(∴k_{P_2 B}=\tan ⁡∠P_2 BO=-\dfrac{1}{3}\)，
又\(B(4，0)\)，\(∴\)直线\(EB\)的方程为\(y= \dfrac{1}{3} x-\dfrac{4}{3}\)，
联立\(\left\{ \begin{array}{c} y=-\dfrac{1}{2} x^2+\dfrac{3}{2} x+2\\ y= \dfrac{1}{3} x-\dfrac{4}{3} \end{array} \right.\)，解得：\(\left\{ \begin{array}{c} x=-\dfrac{5}{3}\\ y=-\dfrac{17}{9} \end{array} \right.\)，即点\(P_2\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．
综上所述，点\(P\)坐标为\((-\dfrac{5}{3} ，-\dfrac{17}{9} )\)．