新定义（24年台州一中自主招生第25题）

专题：新定义 \(\qquad \qquad \qquad \qquad\) 题型：二次函数+相似 \(\qquad \qquad \qquad \qquad\)难度系数：★★★★

 

【题目】

(24年台州一中自主招生第25题) 定义：若一个四边形的面积被一条对角线平分，则称这样的四边形为分积四边形，这条对角线为分积线．
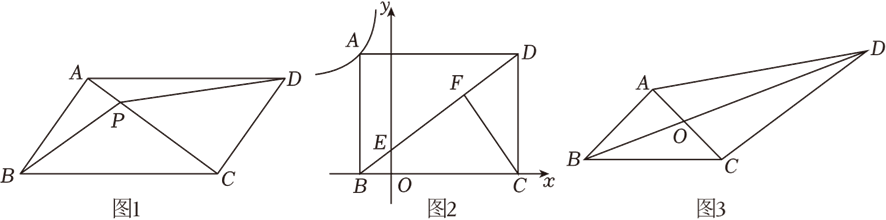
(1)如图1，\(▱ABCD\)中，\(P\)为对角线\(AC\)上一点．求证：四边形\(PBCD\)为分积四边形；
(2)如图2，矩形\(ABCD\)的顶点\(A\)在函数\(y= \dfrac{k}{x}(k<0,x<0)\)的图象上，边\(BC\)在\(x\)轴上，连结对角线\(BD\)交\(y\)轴于点\(E\)，点\(F\)为对角线\(BD\)上一点，若\(DF=(1-k)BE\)，\(△FDC\)的面积为\(6\)，求\(k\)的值；
(3)如图3，四边形\(ABCD\)为分积四边形，对角线\(BD\)为分积线，\(AB=AC\)，\(∠BAC=90^\circ\)，对角线\(BD\)与\(AC\)交于点\(O\)，若\(\dfrac{OD}{OB}=t\)，\(\dfrac{CD^2}{AD^2}=s\)，求\(s\)与\(t\)的关系式并求出\(s\)的取值范围．

 
 
 
 
 

【分析】

第一问： 根据新定义，只需证明\(S_{△BPC}=S_{△DPC}\)，而它们有公共边\(PC\)，那只需证明它们对应高相等便可；

 

第二问： 先分析已知条件
① 点\(A\)在函数\(y=\dfrac{k}{x}\)上

可得到\(OB\times AB=-k\)或\(S_{△ABO}=-\dfrac{k}{2}\)或设点\(A(m，\dfrac{k}{m})\)等；

②\(DF=(1-k)BE\)

会想到找相似三角形(过点\(F\)作\(FH⊥AD\)，则\(△BOE≅△DHF\)，进而得到对应边的比例)，或三角形的面积比例(\(\dfrac{S_{△ABE}}{S_{△ADF} }= \dfrac{BE}{DF}= \dfrac{1}{1-k}\))；
③\(S_{△DCF}=6\)

意识到“第一问为第二问服务”，易想到连接\(AF\)，得到\(S_{△ADF}=S_{△DCF}=6\)；

分析求证：只需要得到关于\(k\)的方程.
串联起来易得思路：\(OB\times AB=-k⇒S_{△ABE}=-\dfrac{k}{2}\)，\(\dfrac{S_{△ABE}}{S_{△ADF} }= \dfrac{BE}{DF}= \dfrac{1}{1-k} ⇒S_{△ABE}=\dfrac{6}{1-k}\)，得方程\(-\dfrac{k}{2}=\dfrac{6}{1-k}\)，求解便可.
当然也可尝试相似三角形的方法，而设点坐标方法比较麻烦.

 

第三问： 分析已知条件
① 四边形\(ABCD\)为分积四边形，对角线\(BD\)为分积线
根据定义可得\(S_{△ABD}=S_{△BCD}\)，进而得到点\(A\)到\(BD\)的距离\(AE\)等于点\(C\)到\(BD\)的距离\(CF\)，

由\(8\)字型，易得\(OA=OC\)；

②\(AB=AC\)，\(∠BAC=90^\circ\)
三角形\(ABC\)是等腰直角三角形，而由①\(O\)是\(AC\)中点，图中较多边存在相等或倍数关系，

则可设\(AO=m\)，\(OC、AB、OB、BC\)能用\(m\)表示，
③\(\dfrac{OD}{OB}=t\)，\(\dfrac{CD^2}{AD^2}=s\)
由②得\(OB=\sqrt5m\)，\(OD=\sqrt5mt\)；而\(\dfrac{CD^2}{AD^2}=s=(\dfrac{CD}{AD})^2\)，即只需要得到\(\dfrac{CD}{AD}\)的表示即可，

会想到相似三角形或两个三角形面积之比，尝试找对应三角形，都不太好弄；发现射影图，问题好解决很多：

便意识到图中很多线段都能够用\(m\)，\(t\)表示出来；
得到\(s\)与\(t\)的关系后，再用函数思想把\(s\)的范围求得.
 

【解答】

第一问 ： 方法1 证明：\(∵ABCD\)是平行四边形，

\(∴△ABC≅△CDA\)，
\(∴\)对应边\(PC\)上的高相等，
\(∴S_{△BPC}=S_{△DPC}\)，
\(∴\)四边形\(PBCD\)为分积四边形．

方法2 证明：\(∵\)平行四边形为中心对称图形，

\(∴S_{△ABC}=S_{△CDA}\)．
\(∵ \dfrac{S_{△BPC}}{S_{△ABC}}= \dfrac{PC}{AC}\)，\(\dfrac{S_{△DPC}}{S_{△CDA}}= \dfrac{PC}{AC}\)，
\(∴S_{△BPC}=S_{△DPC}\)．
\(∴\)四边形\(PBCD\)为分积四边形．
 

第二问 ： 解：如图，连接\(AF\)，\(AE\)．

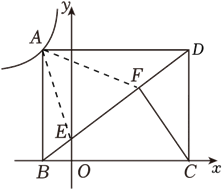
根据反比例函数图象的性质，\(BO\times AB=-k\)，
\(∵\)四边形\(ABCD\)是矩形，
\(∴\)四边形\(ABCF\)为分积四边形．
\(∴S_{△ABF}=S_{△BCF}\)．
\(∴S_{△ADF}=S_{△DCF}=6\)．
\(∵S_{△ABE}=\dfrac{BE}{DF}\times S_{△ADF}=\dfrac{6}{1-k}\)，\(S_{△ABE}=\dfrac{1}{2} AB\times BO=-\dfrac{k}{2}\)．
\(∴\dfrac{6}{1-k}=-\dfrac{k}{2}\)，解得：\(k=-3\)(舍去\(k=4\))．
故\(k\)的值为\(-3\)．
 

第三问 ： 解：过点\(A\)、\(C\)分别向\(BD\)作垂线，\(E\)、\(F\)分别为垂足，则\(AE∥CF\)．

根据分积四边形的定义，得\(S_{△ABD}=S_{△CBD}\)，即\(\dfrac{1}{2} AE\times BD= \dfrac{1}{2} CF\times BD\)，
\(∴AE=CF\)，
易得\(△AOE≅△COF\)，
\(∴AO=OC\)，\(OE =OF\)．
设\(AB=AC=2m\)，则\(AO=OC=m\)，
则\(BO=\sqrt{AB^2+AO^2}=\sqrt5m\)，\(OD=tBO=\sqrt5mt\)，
\(∵AE=AB\times \sin∠ABO=2m\times \dfrac{AO}{BO}=\dfrac{2\sqrt5}{5} m\)，
\(OE=OF=AO\times \cos∠AOB=m\times \dfrac{AO}{BO}=\dfrac{\sqrt5}{5} m\)，(利用三角函数，过程显得更简洁)
\(∴DE=OD+OE=\sqrt5mt+\dfrac{\sqrt5}{5} m\)，
\(DF=OD-OF=OD-OE=\sqrt5mt-\dfrac{\sqrt5}{5} m\)，
\(∴AD^2=AE^2+DE^2= \dfrac{4}{5}m^2+5m^2 t^2+2m^2 t+ \dfrac{1}{5} m^2=m^2+5m^2 t^2+2m^2 t\)，
\(CD^2=CF^2+DF^2= \dfrac{4}{5}m^2+5m^2 t^2-2m^2 t+ \dfrac{1}{5} m^2=m^2+5m^2 t^2-2m^2 t\)．
\(∴s= \dfrac{CD^2}{AD^2}= \dfrac{m^2+5m^2 t^2-2m^2 t}{m^2+5m^2 t^2+2m^2 t}= \dfrac{5t^2-2t+1}{5t^2+2t+1}\)，
(接下来求\(s\)的范围，则把\(s=\dfrac{5t^2-2t+1}{5t^2+2t+1}\)看成自变量为\(t\)的函数，一要确定t的范围，二是分离常数法求解)
\(s=\dfrac{5t^2-2t+1}{5t^2+2t+1} = \dfrac{(5t^2+2t+1)-4t}{5t^2+2t+1}=1- \dfrac{4t}{5t^2+2t+1}=1-\dfrac{4}{5t+ \dfrac{1}{t}+2}\)，
(这是分离常数法：处理类似\(\dfrac{ax^2+bx+c}{dx^2+ex+f}\)形式，先把分子化为常数，问题转化为求\(5t+ \dfrac{1}{t}\)的范围)
\(∵t= \dfrac{OD}{OB}>0\)，

\(∴5t+ \dfrac{1}{t}=(\sqrt{5t}- \dfrac{1}{\sqrt{t}})^2+2\sqrt5≥2\sqrt5\)，
(这里用了完全平方公式，也可以利用高中的基本不等式：若\(a>0\)，\(b>0\)，则\(a+b≥2\sqrt{ab}\)；
那\(5t+ \dfrac{1}{t}≥2\sqrt{5t\times \dfrac{1}{t}}=2\sqrt5\)，当\(t=\dfrac{\sqrt5}{5}\)时取到等号)
\(∴5t+ \dfrac{1}{t}+2≥2\sqrt5+2\)，
\(∴0< \dfrac{4}{5t+2+ \dfrac{1}{t}}≤\dfrac{4}{2\sqrt5+2}= \dfrac{\sqrt5-1}{2}\)，
\(∴ \dfrac{3-\sqrt5}{2}≤1-\dfrac{4}{5t+ \dfrac{1}{t}+2}<1\)，
即\(\dfrac{3-\sqrt5}{2}≤s<1\).