圆的动点+定值问题（19年湛江二中自主招生13题）

专题：圆 \(\qquad \qquad \qquad \qquad\) 题型：动点+定值 \(\qquad \qquad \qquad \qquad\)难度系数：★★★★

---

【题目】

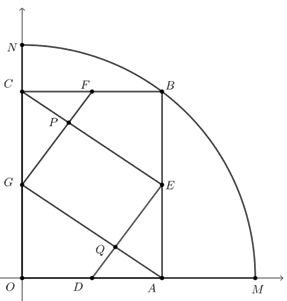
（2019年湛江二中自主招生13题） 如图，扇形\(OMN\)的半径为\(1\)，圆心角是\(90^\circ\)．点\(B\)是\(\overset{\frown}{MN}\)上一动点，\(BA⊥OM\)于点\(A\)，\(BC⊥ON\)于点\(C\)，点\(D、E、F、G\)分别是线段\(OA、AB、BC、CO\)的中点，\(GF\)与\(CE\)相交于点\(P\)，\(DE\)与\(AG\)相交于点\(Q\)．
(1)求证：四边形\(EPGQ\)是平行四边形；
(2)探索当\(OA\)的长为何值时，四边形\(EPGQ\)是矩形；
(3)连结\(PQ\)，试说明\(3PQ^2+OA^2\)是定值．

 
 
 
 

【解答】

第1小问
分析： 由中点想到中位线，第1问较容易想到证明\(GF||DE\)，\(CE||GA\)，从而得到四边形\(EPGQ\)是平行四边形.
证明： 如图①，
\(∵∠AOC=90^\circ\)，\(BA⊥OM\)，\(BC⊥ON\)，

\(∴\)四边形\(OABC\)是矩形．
\(∴AB||OC\)，\(AB=OC\)，
\(∵E\)、\(G\)分别是\(AB、CO\)的中点，

\(∴AE||GC\)，\(AE=GC\)，
\(∴\)四边形\(AECG\)为平行四边形，

\(∴CE||AG\)，
连接\(OB\)，

\(∵\)点\(D、E、F、G\)分别是线段\(OA、AB、BC、CO\)的中点，
\(∴ GF∥OB\)，\(DE∥OB\)，

\(∴ PG∥EQ\)，
\(∴\)四边形\(EPGQ\)是平行四边形．
 

第2小问

分析：
① 若要平行四边形\(EPGQ\)是矩形，方法有二，一是对角线相等\(PQ=GE\)，二是有一个内角是\(90^\circ\)；
② 观察图象，选择后者会容易些，因为图中有较多一线三垂直、A字型与射影定理等几何模型，可利用相似求解；

③ 题中有较多中点，各线段间存在关系，此时利用设元：\(OA=x\)，\(AB=y\)，能够更清晰各线段之间的关系.动点问题要找到源头，本题的源头明显是动点\(B\)，它在\(⊙O\)上，得到\(OB=1\)，即\(x^2+y^2=1\)，利用方程思想，要求\(OA=x\)，只需要由②再得到关于\(x,y\)的一条方程就行.
 

方法一 相似+设元
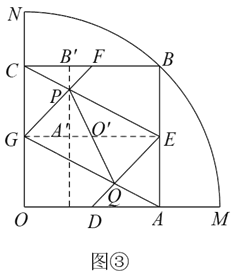
如图②，当\(∠CED=90^\circ\)时，\(□EPGQ\)是矩形．

此时\(∠AED+∠CEB =90^\circ\)，
又\(∵∠DAE=∠EBC =90^\circ\)，\(∴∠AED=∠BCE\)，
\(∴△AED∽△BCE\)，\(∴\dfrac{AD}{BE} =\dfrac{AE}{BC}\)，
设\(OA=x\)，\(AB=y\)，

则\(\dfrac{x}{2} :\dfrac{y}{2} =\dfrac{y}{2} :x\)，得\(y^2=2x^2\)，
又\(OA^2+AB^2=0B^2\)，即\(x^2+y^2=1\)，
\(∴x^2+2x^2=1\)，解得\(x=\dfrac{\sqrt3}{3}\)，
\(∴\)当\(OA\)的长为\(\dfrac{\sqrt3}{3}\)时，四边形\(EPGQ\)是矩形．
(该方法还能用三角函数结合A字型或射影定理求解)
 

方法二 建系法
分析：方法一中用到\(∠CED=90^\circ\)，此时可用到\(k_{CE}⋅k_{ED}=-1\)，便容易想到建系法；
本题源头是动点\(B\)，设\(B(x,y)\)，便也可用方程思想求出\(OA\).
如图以点\(O\)为原点，\(OM、ON\)所在的直线分别为\(x、y\)轴建立直角坐标系，

设\(B(x,y)\)，则\(E(x,\dfrac{1}{2} y)\)，\(C(0,y)\)，\(D(\dfrac{1}{2} x,0)\)，
当\(∠CED=90^\circ\)时，\(□EPGQ\)是矩形，
所以\(k_{CE}⋅k_{ED}=-1\)，

所以\(\dfrac{\dfrac{1}{2}y}{x}\times \dfrac{\dfrac{1}{2}y}{\dfrac{1}{2}x}=-1⇒y^2=2x^2\)①，
又\(OB=1\)，所以\(x^2+y^2=1\)②，
由①②解得\(x=\dfrac{\sqrt3}{3}\)，
\(∴\)当\(OA\)的长为\(\dfrac{\sqrt3}{3}\)时，四边形\(EPGQ\)是矩形．
 

第3小问

分析：接着第2问的思路，设元：\(OA=x\)、\(AB=y\)，本题的关键在于用\(x,y\)表示出\(PQ^2\)，用纯几何的方法要注意四边形\(EPGQ\)是平行四边形和题中已知条件的使用，有些难度；
若用到建系法，求出点\(P、Q\)两点的坐标，再用两点距离公式便可求出\(PQ^2\)；求点\(P\)坐标的思路也不难，求出直线\(CE、GF\)的方程，联系方程便可，求点\(Q\)同理；但是计算量会较大.
 

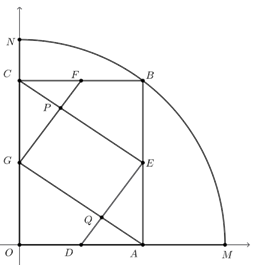
方法一 几何法
如图③，连结\(GE\)交\(PQ\)于\(O'\)，则\(O' P=O'Q\)，\(O' Q=O'E\)，过点\(P\)作\(OC\)的平行线分别交\(BC、GE\)于点\(B'、A'\)．

由\(△PCF∽△PEG\)得\(\dfrac{PG}{PF}= \dfrac{PE}{PC}= \dfrac{GE}{FC}=2\)，
设\(OA=x\)，\(AB=y\)，
\(∴PA'=\dfrac{2}{3} A' B'=\dfrac{1}{3} AB=\dfrac{1}{3} y\)，\(GA'=\dfrac{1}{3} GE=\dfrac{1}{3} OA=\dfrac{1}{3} x\)，
\(∴A'O'=\dfrac{1}{2} GE-GA'=\dfrac{1}{6}OA=\dfrac{1}{6} x\)．
在\(Rt△PA'O'\)中，\(PO'^2=PA'^2+A'O'^2\)，

即\(\dfrac{PQ^2}{4}=\dfrac{AB^2}{9}+\dfrac{OA^2}{36}⟹PQ^2= \dfrac{4}{9} y^2+\dfrac{1}{9} x^2\)，
又\(x^2+y^2=1\)，\(∴3PQ^2=\dfrac{4}{3} (1-x^2 )+\dfrac{1}{3} x^2=\dfrac{4}{3} -x^2\)，
\(∴OA^2+3PQ^2=x^2+\dfrac{4}{3} -x^2=\dfrac{4}{3}\)．
 

方法二 建系法
如图以点\(O\)为原点，\(OM、ON\)所在的直线分别为\(x、y\)轴建立直角坐标系，

设\(B(2m,2n)\)，则\(E(2m,n)\)，\(C(0,2n)\)，\(F(m,2n)\)，\(G(0,n)\)，
设直线\(CE\)的解析式为\(y=kx+b(k≠0)\)，
代入\(E(2m,n)\)，\(C(0,2n)\)，

得到\(\left\{ \begin{array}{c} n=2mk+b\\ 2n=b \end{array} \right. \)，解得\(\left\{ \begin{array}{c} k=- \dfrac{n}{2m}\\ b=2n \end{array} \right. \)，
所以直线\(CE\)的解析式为\(y=- \dfrac{n}{2m} x+2n\)，
(用高中的直线点斜式求解会快些)
同理可得直线\(GF\)的解析式为\(y= \dfrac{n}{m} x+n\)，
由\(\left\{ \begin{array}{c} y= \dfrac{n}{m} x+n\\ y=- \dfrac{n}{2m} x+2n \end{array} \right. \)得\(\left\{ \begin{array}{c} x=\dfrac{2m}{3}\\ y=\dfrac{5n}{3} \end{array} \right. \)，
(此时应该也发现点\(P\)的横坐标处于\(OA\)的\(\dfrac{1}{3}\)处，纵坐标处于\(OC\)的\(\dfrac{5}{6}\)处)
同理可得\(Q(\dfrac{4}{3} m, \dfrac{n}{3})\)，

则\(PQ^2=(\dfrac{4}{3} m-\dfrac{2}{3} m)^2+( \dfrac{n}{3}- \dfrac{5n}{3})^2= \dfrac{4}{9} m^2+ \dfrac{16}{9} n^2\)，
\(∴OA^2+3PQ^2=(2m)^2+\dfrac{4}{3} m^2+ \dfrac{16}{3} n^2= \dfrac{16}{3} m^2+ \dfrac{16}{3} n^2= \dfrac{16}{3}(m^2+n^2)\)，
又\(OB=1\)，

所以\((2m)^2+(2n)^2=1⇒m^2+n^2= \dfrac{1}{4}\)，
\(∴OA^2+3PQ^2= \dfrac{16}{3} (m^2+n^2 )= \dfrac{16}{3}× \dfrac{1}{4}=\dfrac{4}{3}\).